Hopfield神经网络与受限波尔兹曼机

神经网络可分为两大类：

• 一类是多层神经网络、卷积神经网络：可用于模式识别
• 另一类是相互连接型网络：可通过联想记忆去除输入数据中的噪声。

深度学习目录：

1. 自适应线性单元 (Widrow and Hoff, 1960)
2. 神经认知机 (Fukushima, 1980)
3. GPU-加速 卷积网络 (Chellapilla et al., 2006)
4. 深度玻尔兹曼机 (Salakhutdinov and Hinton, 2009a)
5. 无监督卷积网络 (Jarrett et al., 2009b)
6. GPU-加速 多层感知机 (Ciresan et al., 2010)
7. 分布式自编码器 (Le et al., 2012)
8. Multi-GPU 卷积网络 (Krizhevsky et al., 2012a)
9. COTS HPC 无监督卷积网络 (Coates et al., 2013)
10. GoogLeNet (Szegedy et al., 2014a)

Hopfield神经网络 HNN(Hopfield Neural Network)

1982年Hopfield 提出了Hopfield神经网络，是最典型的相互连接型神经网络。

首先我们来看看脑部神经元结构图

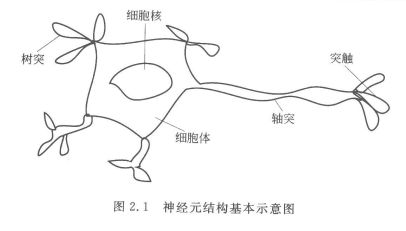
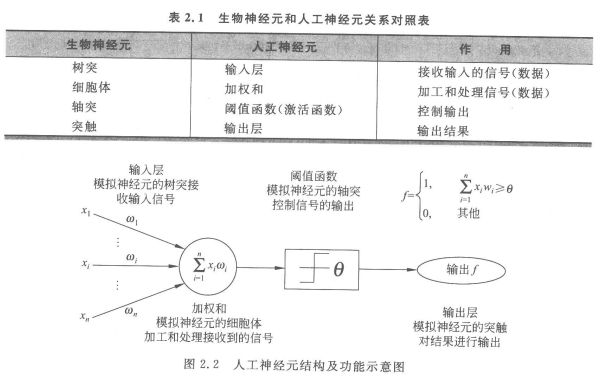
生物神经元和人工神经元的对照关系

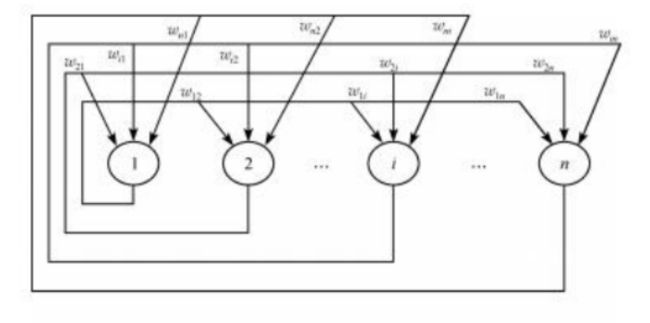
Hopfield神经网络是一种递归神经网络，从输出到输入均有反馈连接，每一个神经元跟所有其他神经元相互连接，又称为全互联网络。
我们根据如上形式，将所有神经元之间两两连接，形成了全互联网络

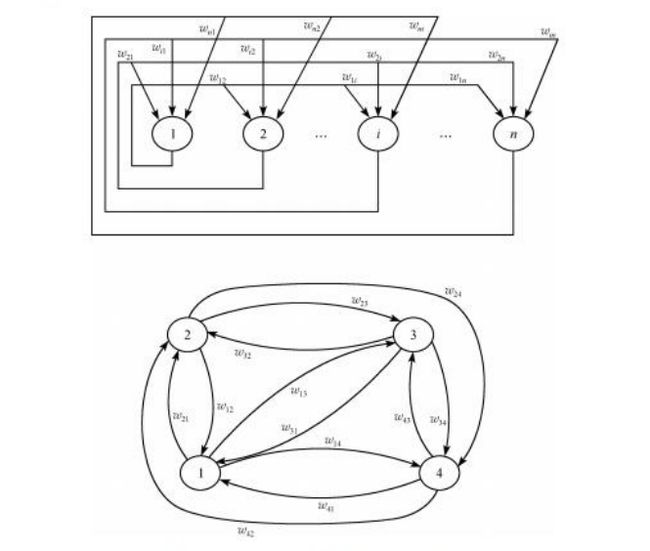
Hopfield最早提出的网络是二值神经网络，各神经元的激励函数为阶跃函数或双极值函数,神经元的输入、输出只取 $(0，1)$ 或者 $(-1，1)$ ，所以也称为离散型Hopfield神经网络DHNN（Discrete Hopfiled Neural Network）

离散Hopfield神经网络DHNN是一个单层网络，有n个神经元节点，每个神经元的输出均接到其它神经元的输入。各节点没有自反馈。每个节点都可处于一种可能的状态（1或－1），即当该神经元所受的刺激超过其阀值时，神经元就处于一种状态（比如1），否则神经元就始终处于另一状态（比如－1）。

构建Hopfield神经网络

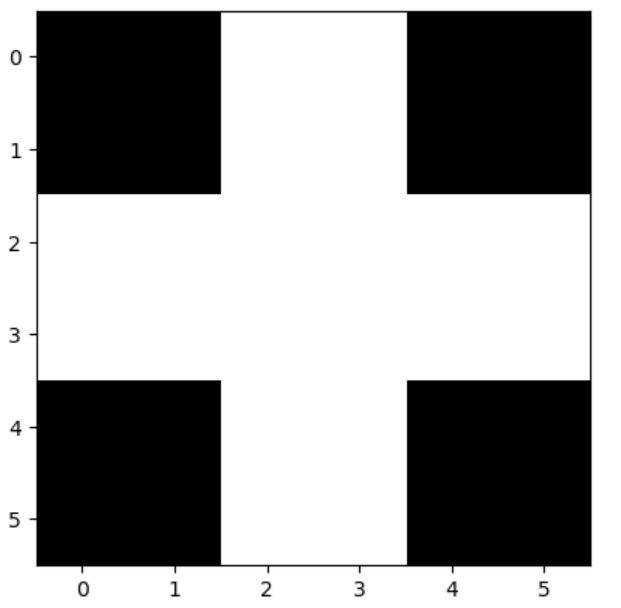
首先，构建Hopfield神经网络需要提供要求记忆的二进制网络，如：

a=np.array([[0,0,1,1,0,0],
            [0,0,1,1,0,0],
            [1,1,1,1,1,1],
            [1,1,1,1,1,1],
            [0,0,1,1,0,0],
            [0,0,1,1,0,0]])

设置神经网络的网络权值

因为网络共有$6\ast 6=36$个结点。故神经网络连接需要$35\ast 35$个（自身与自身不连接）。

我们首先将二维图像展开成为一层

array_a=a.flatten()

其次，设置连接权值。

我们已知Hopfield神经网络为二值神经网络，值为0或1。

设：
$$\begin{gathered} 当a[i]为0，a[j]为1时,权值w_{ij}为-1 \\ 当a[i]为0，a[j]为0时,权值w_{ij}为1 \\ 且w_{ji}=w_{ij} \\ 即：俩结点值相同权值为1，结点不同权值为0 \end{gathered}$$

w=np.zeros((36,36))
for i in range(36):
     for j in range(36):
         if i==j:
             w[i,j]=0
         else:
             w[i,j]=(2*s[i]-1)*(2*s[j]-1)

生成网络权值图如下

输入联想图，开始联想

联想图

c=np.array([[0,0,1,1,0,0],
            [0,0,1,1,0,0],
            [1,1,1,1,1,1],
            [1,1,1,1,1,1],
            [1,0,0,1,0,0],
            [0,0,1,1,0,0]])

开始联想

设输入值为 $x_i(t)$，输出值为 $x_i(t+1)$，$t$ 为迭代次数，有如下公式
$$\begin{gathered} u_i(t)=\sum _{j=1}^n{w}_{ij}{x}_j(t)-b_i(t) \\ {x}_i(t+1)=\{\begin{array}{cc}1& u_i(t)>0\\ x_i(t)(不变)& u_i(t)==0\\ 0& u_i(t)<0\end{array} \end{gathered}$$

• 在此模型中，我们设 $b_i(t)$ 都为0.

依据以上公式，代码如下：

c=c.flatten()
x=c
Y=np.zeros(36)
for t in range(10):
    u = np.zeros(36)
    for j in range(36):
        for i in range(36):
            if i==j:
                u[j]+=0
            else:
                u[j]+=w[i,j]*x[i]
        if u[j]<0:
            Y[j]=0
        else if u[j]==0:
			Y[j] = Y[j];
		else:
            Y[j]=1
    x=Y

输出 $x$

多联想记忆网络

即，一个网络存储多个记忆

将多个记忆的网络权值相加即可。

input_array=[array_a,array_b]
w=np.zeros((36,36))
for s in input_array:
    w0=np.zeros((36,36))
    for i in range(36):
        for j in range(36):
            if i==j:
                w0[i,j]=0
            else:
                w0[i,j]=(2*s[i]-1)*(2*s[j]-1)
    w+=w0

array_b图像

多记忆权值网络：

联想记忆测试a

联想结果a

联想记忆测试b

联想结果b

结果显示，一个网络可以存储多个记忆图。

全部代码

引自：Hopfield神经网络（HNN）详解

import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
a=np.array([[0,0,1,1,0,0],
            [0,0,1,1,0,0],
            [1,1,1,1,1,1],
            [1,1,1,1,1,1],
            [0,0,1,1,0,0],
            [0,0,1,1,0,0]])
b=np.array([[0,0,1,1,0,0],
            [0,1,0,0,1,0],
            [1,0,0,0,0,1],
            [1,0,0,0,0,1],
            [0,1,0,0,1,0],
            [0,0,1,1,0,0]])
c=np.array([[0,0,1,1,0,0],
            [0,0,1,1,0,0],
            [1,1,1,1,1,1],
            [1,1,1,1,1,1],
            [1,0,0,1,0,0],
            [0,0,1,1,0,0]])
array_a=a.flatten()
array_b=b.flatten()
input_array=[array_a,array_b]
w=np.zeros((36,36))
for s in input_array:
    w0=np.zeros((36,36))
    for i in range(36):
        for j in range(36):
            if i==j:
                w0[i,j]=0
            else:
                w0[i,j]=(2*s[i]-1)*(2*s[j]-1)
    w+=w0
c=c.flatten()
v0=c
Y=np.zeros(36)
for t in range(10):
    v1 = np.zeros(36)
    for j in range(36):
        for i in range(36):
            if i==j:
                v1[j]+=0
            else:
                v1[j]+=w[i,j]*v0[i]
        if v1[j]<0:
            Y[j]=0
        else:
            Y[j]=1
    v0=Y
result=np.array(v0).reshape(6,6)
p=Image.fromarray(result*600)
plt.imshow(p)
plt.show()

问题

当需要记忆的模式之间较为相似，或者需要记忆的模式太多，hopfield神经网络就不能正确的辨别模式。这种相互干扰，不能准确记忆的情况称为串扰（crosstalk）。

波尔兹曼机（Boltzmann Machine）

波尔兹曼机与hopfield神经网络的区别

相同处：

• 各单元连接权重是对称的。
• 没有到自身的连接。
• 每个单元的输出要么是0，要么是1。

区别：

• hopfield神经网络的输出是按照某种确定性决定的
• 玻尔兹曼机的输出是按照某种概率分布决定的

受限玻尔兹曼机

简单了解：一起读懂传说中的经典：受限玻尔兹曼机

机器学习笔记之深度玻尔兹曼机(一)玻尔兹曼机系列整体介绍

网络上关于玻尔兹曼机的资料甚少，而且各资料之间有差异，大多全是公式。

我也没有弄明白！