# 数值计算:三角形积分
Python微信订餐小程序课程视频
https://edu.csdn.net/course/detail/36074
Python实战量化交易理财系统
https://edu.csdn.net/course/detail/35475
数值计算:三角形积分
书接上回《高斯-勒朗德积分公式》
**需求:**在给定空间三角形ΔABCΔABC\Delta ABC中,A(x1,y1,z1),B(x2,y2,z2),C(x3,y3,z3)A(x1,y1,z1),B(x2,y2,z2),C(x3,y3,z3)A(x_1,y_1,z_1),B(x_2,y_2,z_2),C(x_3,y_3,z_3),已知函数f(x,y,z)f(x,y,z)f(x,y,z),求利用数值方法求解积分:∬ΔABCf(x,y,z)dS∬ΔABCf(x,y,z)dS\iint_{\Delta ABC}f(x,y,z)\text dS。
**解决方法:**参考triangle_lyness_rule给出的积分方法,具体细节也不是太懂,但是思路上与高斯积分类似,计算平面上的积分点与系数权重进行积分
三角形积分点与积分权重计算
Triangle Llyness Rule
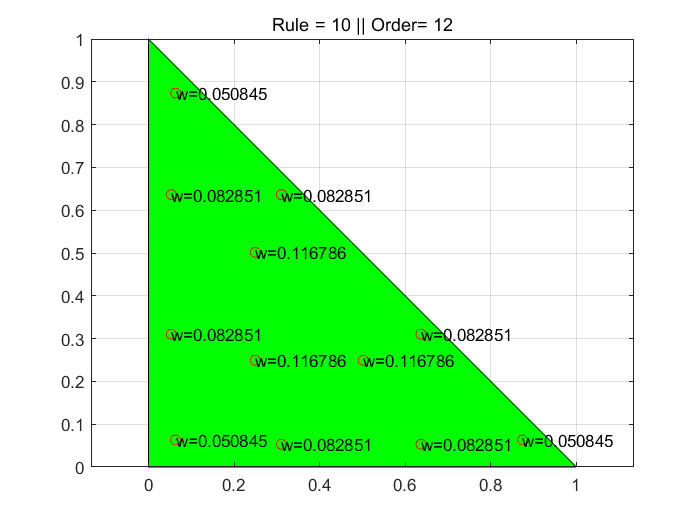
triangle_lyness_rule中给出了不同阶数下,在标准三角形中的系数点位置与权重系数。例如下图中展示Rule=10Rule=10Rule=10时的积分点位置与权重系数。下表中显示了不同RuleRuleRule下的积分精度PrecisionPrecisionPrecision积分点数目orderorderorder以及积分点是否包含三角形中心centercentercenter。
| Rule | Order | Precision | Center |
|---|---|---|---|
| 0 | 1 | 1 | YES |
| 1 | 3 | 2 | NO |
| 2 | 4 | 2 | YES |
| 3 | 4 | 3 | YES |
| 4 | 7 | 3 | YES |
| 5 | 6 | 4 | NO |
| 6 | 10 | 4 | YES |
| 7 | 9 | 4 | NO |
| 8 | 7 | 5 | YES |
| 9 | 10 | 5 | YES |
| 10 | 12 | 6 | NO |
| 11 | 16 | 6 | YES |
| 12 | 13 | 6 | YES |
| 13 | 13 | 7 | YES |
| 14 | 16 | 7 | YES |
| 15 | 16 | 8 | YES |
| 16 | 21 | 8 | NO |
| 17 | 16 | 8 | YES |
| 18 | 19 | 9 | YES |
| 19 | 22 | 9 | YES |
| 20 | 27 | 11 | NO |
| 21 | 28 | 11 | YES |
坐标变换
采用与之前文章中《高斯-勒朗德积分公式》形函数方式计算坐标转换关系。得到三节点形函数为,剩下步骤与《高斯-勒朗德积分公式》中类似。
⎧⎩⎨N1(s,t)=1−s−tN2(s,t)=sN3(s,t)=t{N1(s,t)=1−s−tN2(s,t)=sN3(s,t)=t\begin{cases}
N_1(s,t)=1-s-t\
N_2(s,t)=s\
N_3(s,t)=t\
\end{cases}\
改进
在KY师兄指点下,以上步骤可以进一步简化。原因在于三角形坐标变换的形函数简单,可以直接进行坐标运算,Jacobi系数直接等于三角形面积,具体见代码。
积分测试
以下为测试积分函数,其中LYNESSRULE.txtLYNESSRULE.txtLYNESS_RULE.txt存储的数据太长了,就放到Gitee:链接待更新仓库了。
%% 测试三角形积分
clc;clear;
global TriCoeff
% 导入积分系数
TriCoeff=loadLynessFromTxT("LYNESS_RULE.txt");
P1=[0,0,0];
P2=[2,0,0];
P3=[0,3,0];
% 积分函数
func=@(x,y,z) (x^6+y^3+1);
count=1;
for rule=0:1:21
[P_W] = getTrianglePoints([P1;P2;P3],rule);
[N,~]=size(P_W);
res=0;
for i=1:1:N
res=res+func(P\_W(i,1),P\_W(i,2),P\_W(i,3))*P\_W(i,4);
end
resA(count,1)=res;
resA(count,2)=rule;
resA(count,3)=N;
count=count+1;
end
%% matlab 自带积分函数
pfun = @(x,y) (x.^6+y.^3+1);
xmin = 0;
xmax = 2;
ymin = 0;
ymax = @(x) -3/2*x+3;
r = integral2(pfun,xmin,xmax,ymin,ymax);
%% plot
figure(22)
plot(resA(:,2),resA(:,1),'r-o');hold on;
plot(resA(:,2),r*ones(22,1),'b-');grid on;
xticks([0:2:22]);
xlim([0,22]);
legend("TRIANGLE LYNESS RULE 积分","Matlab integral2积分");
text(10,14,"积分函数:(x^6+y^3+1)")
text(10,12,"积分区域:(0,0,0),(2,0,0),(0,3,0)");
xlabel("Lyness Rule");
ylabel("积分数值");
积分结果对比
代码
getTrianglePoints.m
function [P_W] = getTrianglePoints(Triangle,Rule)
% getTrianglePoints 三角形面元积分
% https://people.sc.fsu.edu/~jburkardt/cpp\_src/triangle\_lyness\_rule/triangle\_lyness\_rule.html
% 输入:
% Triangle(3,3):三角形面元三个点
% Rule:triangle\_lyness\_rule
% 输出:
% P\_W(:,4):P\_W(:,1:3)积分点、P\_W(:,4)权重系数
%% 任意空间三角形 =》平面直角三角形 坐标转换
% 形函数
N1=@(s,t) -s-t+1;
N2=@(s,t) s;
N3=@(s,t) t;
N1_s=@(s,t) -1;
N2_s=@(s,t) 1;
N3_s=@(s,t) 0;
N1_t=@(s,t) -1;
N2_t=@(s,t) 0;
N3_t=@(s,t) 1;
P1=Triangle(1,:);
P2=Triangle(2,:);
P3=Triangle(3,:);
global TriCoeff;
data=TriCoeff{Rule+1,1};
[order,~]=size(data);
P_W=zeros(order,4);
for i=1:1:order
P\_W(i,1:3)=Loc2Glo(data(i,1:2));
P\_W(i,4)=data(i,3)*Jacobi(data(i,1:2));
end
function Pglobal=Loc2Glo(loc)
%loc(1,2)
Pglobal=N1(loc(1),loc(2))*P1+...
N2(loc(1),loc(2))*P2+...
N3(loc(1),loc(2))*P3;
end
function J=Jacobi(Loc)
s=N1\_s(Loc(1),Loc(2))*P1+...
N2\_s(Loc(1),Loc(2))*P2+...
N3\_s(Loc(1),Loc(2))*P3;
t=N1\_t(Loc(1),Loc(2))*P1+...
N2\_t(Loc(1),Loc(2))*P2+...
N3\_t(Loc(1),Loc(2))*P3;
%三角形,这里多除了一个2
J=norm(cross(s,t))/2;
end
end
getTrianglePointsSimplified.m
function [P_W] = getTrianglePointsSimplified(Triangle,Rule)
global TriCoeff;
points = TriCoeff{Rule+1};
weights = points(:,3)';
points(:,3) = 1-points(:,1)-points(:,2);
P_W = zeros(size(points,1),4);
P\_W(:,1:3)=points*Triangle;
area = 0.5*norm(cross(Triangle(1,:)-Triangle(2,:),Triangle(1,:)-Triangle(3,:)));
P\_W(:,4)=weights*area;
end
loadLynessFromTxT.m
function TriCoeff = loadLynessFromTxT(filename)
%LOADLYNESSFROMTXT 加载系数
TriCoeff=cell(22,1);
fp=fopen(filename,'r');
data=textscan(fp,"%f,%f,%f");
fclose(fp);
ALL=[data{1,1},data{1,2},data{1,3}];
[N,~]=size(ALL);
i=1;
while i