【LeetCode226. 翻转二叉树】—— 二叉树遍历

226. 翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

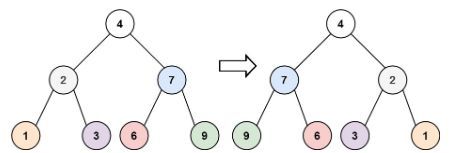
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

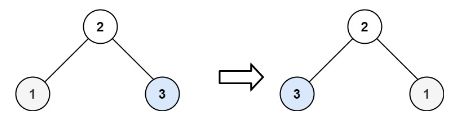
输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目范围在 [0, 100] 内
• -100 <= Node.val <= 100

思考：

本题的要求是将同一“层”上的左右结点进行翻转操作，其实本质上还是对二叉树的遍历，在遍历的过程中添加一个翻转结点的操作即可。

而二叉树的遍历又有着很多种方式，有广度优先遍历以及深度优先遍历，深度优先遍历又分为前序遍历、中序遍历、后序遍历三种，而其中，只有中序遍历不适合解该题，因为中序遍历的中间结点位于中间，不方便将其前后的左右结点进行翻转操作。

而各种遍历中，又分别可以使用递归法以及迭代法进行实现，递归法比较简洁，但相对来讲难以理解。迭代法便于理解，但较为繁琐。

递归法：

首先让我们使用递归法进行求解。

前序遍历：

我们可以先来看看二叉树的前序遍历是怎么完成的：

class Solution {
public:
    void traversal(TreeNode* cur, vector<int>& vec)
    {
        if (cur == NULL)
        {
            return;
        }
        vec.push_back(cur->val);
        traversal(cur->left, vec);
        traversal(cur->right, vec);
    }
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        traversal(root, result);
        return result;
    }
};

而在本题中，我们所要返回的只是在完成翻转后的二叉树根结点，并且在每一轮遍历时进行交换结点的操作即可：

class Solution {
public:
    void traversal(TreeNode* cur)
    {
        if (cur == NULL)
        {
            return;
        }
        swap(cur->left,cur->right);
        traversal(cur->left);
        traversal(cur->right);
    }
    TreeNode* invertTree(TreeNode* root) {
        traversal(root);
        return root;
    }   
};

当然，我们可以进一步简化代码使两个函数“合二为一”。

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == NULL)
        {
            return root;
        }
        swap(root->left, root->right);
        invertTree(root->left);
        invertTree(root->right);
        return root;
    }   
};

后续遍历：

同理我们可以写出后续遍历：

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == NULL)
        {
            return root;
        }
        invertTree(root->left);
        invertTree(root->right);
        swap(root->left, root->right);
        return root;
    }
};

中序遍历：

利用中序遍历时需要多加注意，因为是在中间进行节点交换的操作，所以在交换后仍然要遍历左节点，即原来的右节点。

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == NULL) return root;
        invertTree(root->left);         // 左
        swap(root->left, root->right);  // 中
        invertTree(root->left);         // 注意 这里依然要遍历左孩子，因为中间节点已经翻转了
        return root;
    }
};

迭代法：

遍历的方法本就有递归法和迭代法两种，接下来就尝试用迭代法进行遍历：

前序遍历：

迭代法的前序遍历如下：使用了栈这种数据结构，利用其先进后出的特性，完成遍历。

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == NULL) return root;
        stack<TreeNode*> st;
        st.push(root);
        while(!st.empty()) {
            TreeNode* node = st.top();              // 中
            st.pop();
            swap(node->left, node->right);
            if(node->right) st.push(node->right);   // 右
            if(node->left) st.push(node->left);     // 左
        }
        return root;
    }
};

层序遍历：

层序遍历，即深度优先遍历，也可以很容易进行求解，层序遍历使用的是队列这一种数据结构：

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        while (!que.empty()) {
            int size = que.size();
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                swap(node->left, node->right); // 节点处理
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return root;
    }
};

参考：代码随想录

往期回顾：
专题一 二叉树层序遍历
LeetCode102. 二叉树的层序遍历
LeetCode144、145、94. 二叉树遍历
LeetCode18. 四数之和
LeetCode15. 三数之和
LeetCode383. 赎金信
LeetCode454. 四数相加 II
LeetCode1. 两数之和
LeetCode202. 快乐数
LeetCode350. 两个数组的交集 II
LeetCode349. 两个数组的交集
LeetCode1002. 查找共用字符