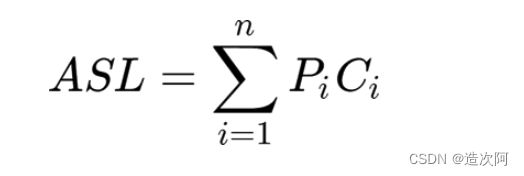算法百花齐放：探索常见算法的精妙之道

在计算机科学的领域中，算法是一项关键而令人着迷的技术。它们是解决问题、优化效率以及创造智能系统的核心。从简单的排序和搜索任务到复杂的机器学习和深度学习应用，常见算法为我们提供了解决各种挑战的有力工具。在本篇博客中，我们将探索常见算法的精妙之道！本篇博客主要讲解冒泡排序、二分法查找（折半查找）等常见的算法。

大家如果想更好的理解，可以看这个网站（上面可以根据程序执行看到动画效果）：https://visualgo.net/

⭐ 冒泡排序算法

冒泡排序算法

冒泡排序是最常用的排序算法，在笔试中也非常常见，能手写出冒泡排序算法可以说是基本的素养。本节讲解冒泡的基础算法和优化算法，既提高大家算法的素养，也可以从容面对找工作时 JAVA 的笔试题目。

冒泡排序的基础算法

冒泡排序算法重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来，这样越大的元素会经由交换慢慢“浮”到数列的顶端。

冒泡排序算法的运作如下：

1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
3. 针对所有的元素重复以上的步骤，除了最后一个。
4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

【eg】冒泡排序的基础算法

import java.util.Arrays;
	public class TestBubbleSort {
		public static void main(String[ ] args) {
			int[ ] values = { 3, 1, 6, 8, 9, 0, 7, 4, 5, 2 };
			bubbleSort(values);
		System.out.println(Arrays.toString(values));
	}
		public static void bubbleSort(int[ ] values) {
			int temp;
			for (int i = 0; i < values.length; i++) {
			for (int j = 0; j < values.length - 1 - i; j++) {
			if (values[j] > values[j + 1]) {
			temp = values[j];
			values[j] = values[j + 1];
			values[j + 1] = temp;
				}
			}
		}
	}
}

冒泡排序的优化算法

我们可以把上面的冒泡排序的算法优化一下，基于冒泡排序的以下特点：

1.整个数列分成两部分：前面是无序数列，后面是有序数列。
2.判断每一趟是否发生了数组元素的交换，如果没有发生，则说明此时数组已经有序，无需再进行后续趟数的比较了。此时可以中止比较。

【eg】冒泡排序的优化算法

import java.util.Arrays;
	public class TestBubbleSort2 {
		public static void main(String[ ] args) {
			int[ ] values = { 3, 1, 6, 8, 9, 0, 7, 4, 5, 2 };
			bubbleSort(values);
			System.out.println(Arrays.toString(values));
	}
		public static void bubbleSort2(int[ ] values) {
			int temp;
			for (int i = 0; i < values.length ; i++) {
// 定义一个布尔类型的变量，标记数组是否已达到有序状态
			boolean flag = true;
	/*内层循环：每一趟循环都从数列的前两个元素开始进行比较，比较到无序数组的最后*/
			for (int j = 0; j < values.length - 1 - i; j++) {
// 如果前一个元素大于后一个元素，则交换两元素的值；
			if (values[j] > values[j + 1]) {
			temp = values[j];
			values[j] = values[j + 1];
			values[j + 1] = temp;
 //本趟发生了交换，表明该数组在本趟处于无序状态，需要继续比较；
			flag = false;
	}
}
 //根据标记量的值判断数组是否有序，如果有序，则退出；无序，则继续循环。
			if (flag) {
			break;
			}
		}
	}
}

执行结果如下所示：

冒泡排序的特点及性能

通过冒泡排序的算法思想，我们发现冒泡排序算法在每轮排序中会使一个元素排到一端，也就是最终需要 n-1 轮这样的排序（n 为待排序的数列的长度），而在每轮排序中都需要对相邻的两个元素进行比较，在最坏的情况下，每次比较之后都需要交换位置，所以这里的时间复杂度是 O(n²)。其实冒泡排序在最好的情况下，时间复杂度可以达到 O(n)，这当然是在待排序的数列有序的情况下。在待排序的数列本身就是我们想要的排序结果时，时间复杂度的确是 O(n)，因为只需要一轮排序并且不用交换。但是实际上这种情况很少，所以冒泡排序的平均时间复杂度是 O(n²)。

对于空间复杂度来说，冒泡排序用到的额外的存储空间只有一个，那就是用于交换位置的临时变量，其他所有操作都是在原有待排序列上处理的，所以空间复杂度为 O(1)。

冒泡排序是稳定的，因为在比较过程中，只有后一个元素比前面的元素大时才会对它们交换位置并向上冒出，对于同样大小的元素，是不需要交换位置的，所以对于同样大小的元素来说，相对位置是不会改变的。

冒泡排序算法的时间复杂度其实比较高。从 1956 年开始就有人研究冒泡排序算法，后续也有很多人对这个算法进行改进，但结果都很一般，正如 1974 年的图灵奖获得者所说的：“冒泡排序除了它迷人的名字和引起的某些有趣的理论问题，似乎没有什么值得推荐的。”

冒泡排序的适用场景

对于冒泡排序，我们应该对它的思想进行理解，作为排序算法学习的引导，让我们的思维更加开阔。

虽然冒泡排序在我们的实际工作中并不会用到，其他排序算法多多少少比冒泡排序算法的性能更高，但是我们还是要掌握冒泡排序的思想及实现，并且在面试时还是有可能会用到。

⭐ 二分法查找（折半查找）

二分法检索（binary search）又称折半检索（折半查找）。

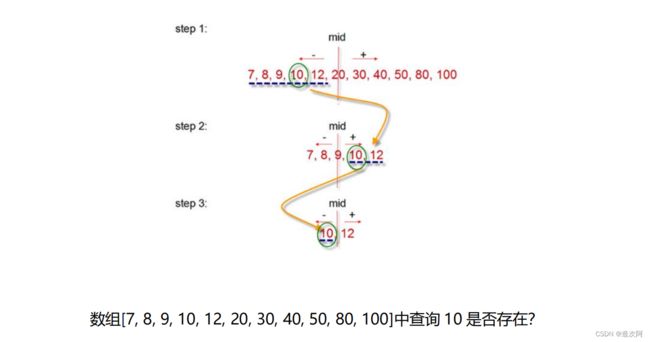
二分法检索的基本思想是设数组中的元素从小到大有序地存放在数组（array）中，首先将给定值 key 与数组中间位置上元素的关键码(key)比较，如果相等，则检索成功；

否则，若 key 小，则在数组前半部分中继续进行二分法检索;

若 key 大，则在数组后半部分中继续进行二分法检索。

这样，经过一次比较就缩小一半的检索区间，如此进行下去，直到检索成功或检索失败。

二分法检索是一种效率较高的检索方法。

【eg】二分法查找法的基本算法

import java.util.Arrays;
	public class TestBinarySearch {
		public static void main(String[ ] args) {
			int[ ] arr = { 30,20,50,10,80,9,7,12,100,40,8};
			int searchWord = 20; // 所要查找的数
			Arrays.sort(arr); //二分法查找之前，一定要对数组元素排序
		System.out.println(Arrays.toString(arr));
		System.out.println(searchWord+"元素的索引："+binarySearch(arr,searchWord));
	}
		public static int binarySearch(int[ ] array, int value){
		 	int low = 0;
 			int high = array.length - 1;
 			while(low <= high){
 			int middle = (low + high) / 2;
 			if(value == array[middle]){
 			return middle; //返回查询到的索引位置
	 }
			if(value > array[middle]){
 			low = middle + 1;
 	}
 			if(value < array[middle]){
 			high = middle - 1;
 	}
 }
			return -1; //上面循环完毕，说明未找到，返回-1
 	}
}

执行结果如下所示：

二分查找算法的性能分析

衡量二分查找算法的性能，可以计算它的时间复杂度，也可以计算它的平均查找长度（ASL）。

二分查找算法的时间复杂度可以用O(log2n)表示（n 为查找表中的元素数量，底数 2 可以省略）。和顺序查找算法的O(n)相比，显然二分查找算法的效率更高，且查找表中的元素越多，二分查找算法效率高的优势就越明显。

计算二分查找算法的平均查找长度，可以借助下面给出的公式：

默认情况下，表中各个元素被查找到的概率是相同的，都是 1/n（n 为查找表中元素的数量），所以各个元素对应的 Pi 都是 1/n。

二分查找过程中，各个元素对应的查找次数 Ci 可以借助一棵二叉树直观地看出来，通常称为“判定树”。

当查找表中的元素足够多时（n足够大），二分查找算法对应的 ASL 值近似等于 log2(n+1)-1。

和顺序查找算法对应的 ASL 值 (n+1)/2 相比，二分查找算法的 ASL 值更小，可见后者的执行效率更高。

注意：

二分查找算法的时间复杂度为O(logn)，平均查找长度 ASL=log2(n+1)-1。和前面章节讲解的顺序查找算法相比，二分查找算法的执行效率更高。

二分查找算法只适用于有序的静态查找表，且通常选择用顺序表表示查找表结构。

在这篇博客中，我们探索了常见算法的精妙之道，让我们的思维在数学与计算的交织中激荡出绚丽的火花。从排序算法的优雅舞蹈，到查找算法的神奇探险，我们领略了算法设计的艺术之美。

算法世界如同一片广袤的花海，每一种算法都是一朵独特的花朵，各自绽放着自己的光彩。正如百花齐放，每种算法都有其独特的应用领域和优势。在这个多元化的算法宇宙中，我们应该秉持开放的心态，不断学习和探索。

与算法相伴的还有数据结构，它们如同花瓣一样，为算法提供了坚实的基础和高效的操作方式。我们的学习之旅还远未结束，数据结构与算法的奇妙组合将继续引领我们走向新的思维境地。

在这个充满挑战和机遇的时代，掌握精妙的算法之道是非常重要的。无论是在工程开发中提升效率，还是在解决实际问题中寻找最优解，算法都是我们的得力助手。

让我们共同追求算法的卓越，探索更多未知的领域。在百花齐放的世界里，让我们的思维不断绽放，创造出更加美妙和智慧的未来！

谢谢您的阅读与关注！

愿编程之花永远绽放！