电子技术——伪NMOS逻辑电路
电子技术——伪NMOS逻辑电路
伪NMOS逻辑反相器
下图展示了从CMOS修改而来的CMOS反相器:
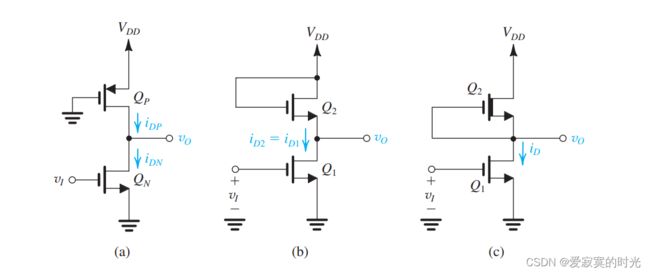
在这里只有 Q N Q_N QN 接入输入端电压,同时 Q P Q_P QP 接地。 Q P Q_P QP 相当于是 Q N Q_N QN 的负载。当我们深入研究这个电路之前,首先这个电路存在一个显然的优点:每一个输入变量只连接了一个晶体管。因此受到扇入效应影响的传播延迟可以得到改善。
图(a)很像CMOS反相器,因此我们称为伪NMOS逻辑反相器。为了比较,我们将简短的介绍一下伪NMOS逻辑反相器两个旧的形式。最早的使用增强型MOSFET作为负载,如图(b)。这个电路的缺点是电压摆幅太小,噪声容限太低,具有过高的静态功率耗散。由于以上原因,这种电路已经过时了,在这之后被耗散型NMOS负载所替代了,如图©。
首先,当耗散型NMOS处于 V G S = 0 V_{GS} = 0 VGS=0 的时候,相当于一个恒流源,可以作为一个绝佳的负载源。然而,不久人们意识到耗散型NMOS受到体效应的影响,工作点可能会发生较大的偏移,导致电流源性能下降。虽然耗散型NMOS负载的性能要优于增强型NMOS负载,但是生产耗散型NMOS负载需要额外的步骤和成本。尽管耗散型负载的NMOS已经几乎完全被CMOS所替代,我们依然能够在特定的场合看到耗散型负载的NMOS。基于以上,本书中我们不再讲解耗散型负载的NMOS。
伪NMOS逻辑反相器很像过去的耗散型负载的NMOS,但是性能相对得到提升,而且还可以直接兼容现有的CMOS电路。
静态特性
首先, Q N Q_N QN 的漏极电流为:
i D N = 1 2 k n ( v I − V t ) 2 , v O ≥ v I − V t i_{DN} = \frac{1}{2} k_n (v_I -V_t)^2, v_O \ge v_I - V_t iDN=21kn(vI−Vt)2,vO≥vI−Vt
i D N = k n [ ( v I − V t ) v O − 1 2 v O 2 ] , v O ≤ v I − V t i_{DN} = k_n[(v_I - V_t)v_O - \frac{1}{2}v_O^2], v_O \le v_I - V_t iDN=kn[(vI−Vt)vO−21vO2],vO≤vI−Vt
i D P = 1 2 k p ( V D D − V t ) 2 , v O ≤ V t i_{DP} = \frac{1}{2}k_p(V_{DD} - V_t)^2, v_O \le V_t iDP=21kp(VDD−Vt)2,vO≤Vt
i D P = k p [ ( V D D − V t ) ( V D D − v O ) − 1 2 ( V D D − v O ) 2 ] , v O ≥ V t i_{DP} = k_p[(V_{DD} - V_t)(V_{DD} - v_O) - \frac{1}{2}(V_{DD} - v_O)^2], v_O \ge V_t iDP=kp[(VDD−Vt)(VDD−vO)−21(VDD−vO)2],vO≥Vt
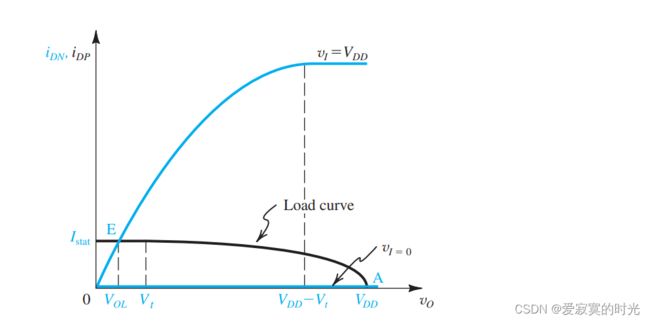
我们在这里假设 V t n = − V t p = V t V_{tn} = -V_{tp} = V_t Vtn=−Vtp=Vt 来简化计算。发现 i D N i_{DN} iDN 和 v I v_I vI 的两个输入状态有关,而 i D P i_{DP} iDP 无关,我们可以做出驱动负载曲线图:
- 负载曲线当 v I = V D D v_I = V_{DD} vI=VDD 的时候表现出一个较小的饱和负载电流,可以在设计上使得 k n k_n kn 比 k p k_p kp 大4-10倍即可。这种反相器称为比例型,并且比例为 r ≡ k n / k p r \equiv k_n / k_p r≡kn/kp 比例参数决定了VTC的全部特征,包括 V O L , V I L , V I H V_{OL},V_{IL},V_{IH} VOL,VIL,VIH 等等,也决定了噪声容限。选择一个较高的 r r r 可以减小 V O L V_{OL} VOL 并且获得一个较大的噪声容限。
- 只有 v O ≤ V t v_O \le V_t vO≤Vt 的时候 Q P Q_P QP 才表现为电流源,其他情况 Q P Q_P QP 将进入三极管区。
考虑两个极端的情况,当 v I = 0 v_I = 0 vI=0 的时候, Q N Q_N QN 截止而 Q P Q_P QP 也工作在截止区,此时没有电流,静态功率为零,对应图中的点A。当 v I = V D D v_I = V_{DD} vI=VDD 的时候,对应于点E。相对于CMOS反相器,此时 V O L V_{OL} VOL 并不等于零,这是一个显然的缺点。另外一个缺点是存在静态功率 P D = I s t a t × V D D P_D = I_{stat} \times V_{DD} PD=Istat×VDD 。
VTC特性
下图展示了伪NMOS的VTC特性曲线:

如图所示,在VTC曲线总共有四个区域,对应了 Q N Q_N QN 和 Q P Q_P QP 的四种的状态不同的区域,如图:
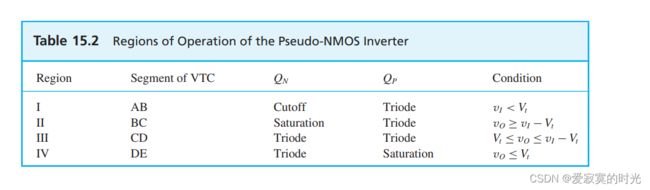
对于区域一(AB段), Q N Q_N QN 截止而 Q P Q_P QP 处于三极管区,此时:
v O = V O H = V D D v_O = V_{OH} = V_{DD} vO=VOH=VDD
对于区域二(BC段), Q N Q_N QN 饱和而 Q P Q_P QP 仍然处于三极管区,通过联立漏极电流方程,假设 k n = r k p k_n = rk_p kn=rkp 我们得到:
v O = V t + ( V D D − V t ) 2 − r ( v I − V t ) 2 v_O = V_t + \sqrt{(V_{DD} - V_t)^2 -r(v_I - V_t)^2} vO=Vt+(VDD−Vt)2−r(vI−Vt)2
我们带入 d v O / d v I = − 1 d v_O / d v_I = -1 dvO/dvI=−1 并且 v I = V I L v_I = V_{IL} vI=VIL :
V I L = V t + V D D − V t r ( r + 1 ) V_{IL} = V_t + \frac{\sqrt{V_{DD} - V_t}}{\sqrt{r(r+1)}} VIL=Vt+r(r+1)VDD−Vt
中点 V M V_M VM 当 v O = v I v_O = v_I vO=vI :
V M = V t + V D D − V t r + 1 V_M = V_t + \frac{\sqrt{V_{DD} - V_t}}{\sqrt{r + 1}} VM=Vt+r+1VDD−Vt
最后,区域二的终点C可以通过带入 v O = v I − V t v_O = v_I - V_t vO=vI−Vt ,这是 Q N Q_N QN 的饱和条件,C点之后进入三极管区。
对于区域三,这个区域我们不感兴趣,终点D可以由 v O = V t v_O = V_t vO=Vt 得到。
对于区域四(DE段),带入漏极电流方程可以得到:
v O = ( v I − V t ) − ( v I − V t ) 2 − 1 r ( V D D − V t ) 2 v_O = (v_I - V_t) - \sqrt{(v_I - V_t)^2 - \frac{1}{r}(V_{DD} - V_t)^2} vO=(vI−Vt)−(vI−Vt)2−r1(VDD−Vt)2
带入 d v O / d v I = − 1 d v_O / d v_I = -1 dvO/dvI=−1 以及 v I = V I H v_I = V_{IH} vI=VIH 得到:
V I H = V t + 2 3 r ( V D D − V t ) V_{IH} = V_t + \frac{2}{\sqrt{3r}}(V_{DD} - V_t) VIH=Vt+3r2(VDD−Vt)
同时带入 v I = V D D v_I = V_{DD} vI=VDD 得到:
V O L = ( V D D − V t ) [ 1 − 1 − 1 r ] V_{OL} = (V_{DD} - V_t)[1 - \sqrt{1 - \frac{1}{r}}] VOL=(VDD−Vt)[1−1−r1]
此时的静态饱和电流为:
I s t a t = 1 2 k p ( V D D − V t ) 2 I_{stat} = \frac{1}{2} k_p (V_{DD} - V_t)^2 Istat=21kp(VDD−Vt)2
最后:
N M L = V t − ( V D D − V t ) [ 1 − 1 − 1 r − 1 r ( r + 1 ) ] NM_L = V_t - (V_{DD} - V_t)[1 - \sqrt{1 - \frac{1}{r}} - \frac{1}{\sqrt{r(r+1)}}] NML=Vt−(VDD−Vt)[1−1−r1−r(r+1)1]
N M H = ( V D D − V t ) ( 1 − 2 3 r ) NM_H = (V_{DD} - V_t) (1 - \frac{2}{\sqrt{3r}}) NMH=(VDD−Vt)(1−3r2)
最后,我们发现 V D D V_{DD} VDD 和 V t V_t Vt 由工艺决定,唯一可以控制的参数是 r r r 。
动态响应
通过平均估计法,我们可以算出:
t P L H = α p C k p V D D t_{PLH} = \frac{\alpha_p C}{k_p V_{DD}} tPLH=kpVDDαpC
这里:
α p = 2 / [ 7 4 − 3 ( V t V D D ) + ( V t V D D ) 2 ] \alpha_p = 2 / [\frac{7}{4} - 3(\frac{V_t}{V_{DD}}) + (\frac{V_t}{V_{DD}})^2] αp=2/[47−3(VDDVt)+(VDDVt)2]
同样的:
t P H L ≃ α n C k n V D D t_{PHL} \simeq \frac{\alpha_n C}{k_n V_{DD}} tPHL≃knVDDαnC
这里:
α n = 2 / [ 1 + 3 4 ( 1 − 1 r ) − ( 3 − 1 r ) ( V t V D D ) + ( V t V D D ) 2 ] \alpha_n = 2 / [1 + \frac{3}{4}(1 - \frac{1}{r}) - (3 - \frac{1}{r})(\frac{V_t}{V_{DD}}) + (\frac{V_t}{V_{DD}})^2] αn=2/[1+43(1−r1)−(3−r1)(VDDVt)+(VDDVt)2]
对于极大的 r r r 我们可以估计:
α n ≃ α p \alpha_n \simeq \alpha_p αn≃αp
尽管伪NMOS反相器的动态响应和CMOS反相器的差不多,但是伪NMOS反相器存在一个特殊的问题,因为 k p k_p kp 比 k n k_n kn 小 r r r 倍。那么 t P L H t_{PLH} tPLH 大约比 t P H L t_{PHL} tPHL 大 r r r 倍。此时电路表现出一种非对称的动态响应。然而,与CMOS反相器相比,伪NMOS反相器的扇入数量更少,因此具有更小的有效电容。
设计
设计伪NMOS逻辑电路包括选择比例 r r r 和每个MOS的宽长比。
- 比例 r r r 决定了VTC曲线中所有的断点。越大的 r r r 那么 V O L V_{OL} VOL 就越小,具有更大的噪声容限,但是越大的 r r r 会使得反相器的动态响应越不对称,对于PMOS需要更大的硅面积。因此,选择 r r r 需要在噪声容限和硅面积和 t P t_P tP 中做出妥协。
- 一旦 r r r 确定,我们可以选择较小的 ( W / L ) n (W/L)_n (W/L)n 来减小器件体积并且能获得一个较小的 C C C 。同样的,较小的 ( W / L ) p (W/L)_p (W/L)p 可以保持较小的 I s t a t I_{stat} Istat 和 P D P_D PD 。另一方面,我们也可以选择较大的 W / L W/L W/L 来获得较低的 t P t_P tP 和更快的响应速度。对于普通(高速)器件, ( W / L ) p (W/L)_p (W/L)p 通常在 50uA 到 100uA 之间,对于 V D D = 1.8 V V_{DD} = 1.8V VDD=1.8V ,此时 P D P_D PD 在 90uW 和 180uW 之间。
门电路
伪NMOS逻辑电路还可以用于门电路,如下图是一个四变量输入的NOR和NAND逻辑门电路:

与CMOS相比,伪NMOS的NOR和NAND只需要五个晶体管即可,而CMOS则需要八个。在伪NMOS逻辑门中,NOR比NAND更受欢迎,因为NOR是晶体管并联结构,可以降低NMOS的尺寸。
总结
伪NMOS逻辑电路适合大部分时间都是高电平输出的逻辑门电路(此时静态功耗为零,只有低电平输出才有静态功耗)。此外,若从高到低的电平跃迁是主要的,那么就可以根据需求降低传播延迟。一种特殊是设计是内存芯片的地址解码器和只读储存器。