0-1背包问题的多种办法求解
目录
一、问题分析
(一)、题目
(二)、问题分析
二、设计思路
1.回溯法
2.分支限界法
3.动态规划
三、算法设计/问题求解特色及关键技术
(一) 算法设计/问题求解特点
(1) 动态规划法:
(2) 回溯法
(3) 分支限界法
四、 算法测试
(一)动态规划法测试时间:
(二) 回溯法运行时间:
(三) 分支限界法运行时间
五、实验体会
一、问题分析
(一)、题目
给定n种物品和一个背包。物品i的重量是Wi,其价值为Vi,背包最大承载重量为C。物品是不可分割的,应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
要求:随机生成物品和背包数据,分别利用回溯法、分支限界法和动态规划三种方法求解该问题并形成解题报告。
(二)、问题分析
不同物体的重量与价值不同,而背包的容量也有限,因此要选择出所有物体总重量不超过背包容量的方案中,价值最大的一个方案;或列出所有方案,计算价值并对其进行排序后,选择最接近且不超过背包容量的一个方案。
二、设计思路
1.回溯法
回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择。
因此使用回溯法时,我们首先进行了子集树的构建,对于每一个物品i,对于该物品只有选与不选2个决策,总共有n个物品,可以顺序依次考虑每个物品,这样就形成了一棵解空间树: 基本思想就是遍历这棵树,以枚举所有情况,最后进行判断,如果重量不超过背包容量,且价值最大的话,该方案就是最后的答案。
2.分支限界法
分支限界法常以广度优先或以最小耗费(最大效益)优先的方式搜索问题的解空间树。在分支限界法中,每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点,就一次性产生其所有子结点。在这些子结点中,导致不可行解或导致非最优解的子结点被舍弃,其余子结点被加入活结点表中。此后,从活结点表中取下一结点成为当前扩展结点,并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止。
于是我们确定了定义解空间、确定解空间、搜索解空间的解题思路顺序来设计算法解决问题。
3.动态规划
动态规划与分治法类似,都是把大问题拆分成小问题,通过寻找大问题与小问题的递推关系,解决一个个小问题,最终达到解决原问题的效果。但不同的是,分治法在子问题和子问题等上被重复计算了很多次,而动态规划则具有记忆性,通过填写表把所有已经解决的子问题答案纪录下来,在新问题里需要用到的子问题可以直接提取,避免了重复计算,从而节约了时间,所以在问题满足最优性原理之后,用动态规划解决问题的核心就在于填表,表填写完毕,最优解也就找到。
基于此,本组根据动态规划解题步骤:问题抽象化、建立模型、寻找约束条件、判断是否满足最优性原理、找大问题与小问题的递推关系式、填表、寻找解组成,找出01背包问题的最优解以及解组成,然后编写代码实现。
三、算法设计/问题求解特色及关键技术
- 算法设计/问题求解特点
- 动态规划法:
动态规划的原理
动态规划与分治法类似,都是把大问题拆分成小问题,通过寻找大问题与小问题的递推关系,解决一个个小问题,最终达到解决原问题的效果。但不同的是,分治法在子问题和子子问题等上被重复计算了很多次,而动态规划则具有记忆性,通过填写表把所有已经解决的子问题答案纪录下来,在新问题里需要用到的子问题可以直接提取,避免了重复计算,从而节约了时间,所以在问题满足最优性原理之后,用动态规划解决问题的核心就在于填表,表填写完毕,最优解也就找到。
该问题的特点是:每种物品一件,可以选择放1或不放0。
随后,建立模型,即求max(V1X1+V2X2+…+VnXn);即为最大价值
寻找约束条件,W1X1+W2X2+…+WnXn
寻找递推关系式,面对当前商品有两种可能性:
第一种:包的容量比该商品体积小,装不下,此时的价值与前i-1个的价值是一样的,即V(i,j)=V(i-1,j);
第二种:还有足够的容量可以装该商品,但装了也不一定达到当前最优价值,所以在装与不装之间选择最优的一个,即V(i,j)=max{V(i-1,j),V(i-1,j-w(i))+v(i)}。
其中V(i-1,j)表示不装,V(i-1,j-w(i))+v(i) 表示装了第i个商品,背包容量减少w(i),但价值增加了v(i);
由此可以得出递推关系式:
j
j>=w(i) V(i,j)=max{V(i-1,j),V(i-1,j-w(i))+v(i)}
————————————————
本问题的关键点在于:用子问题定义状态:即f[i][v]表示前i件物品恰放入一个最大承重为weight的背包可以获得的最大价值。则其状态转移方程便是:
f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]}
关键技术代码如下:
for (int i = 1; i <= 4; i++) {
for (int j = 1; j <= bagW; j++) {
if (j < w[i])
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
}
此外,还有一个和关键点是利用回溯,找到符合条件的最优解并罗列出来。
————————————————
V(i,j)=V(i-1,j)时,说明没有选择第i 个商品,则回到V(i-1,j);
V(i,j)=V(i-1,j-w(i))+v(i)时,说明装了第i个商品,该商品是最优解组成的一部分,随后我们得回到装该商品之前,即回到V(i-1,j-w(i));
一直遍历到i=0结束为止,所有解的组成都会找到。
关键技术代码:
void findWhat(int i, int j) { //最优解情况
if (i >= 0) {
if (dp[i][j] == dp[i - 1][j]) {
item[i] = 0;
findWhat(i - 1, j);
}
else if (j - w[i] >= 0 && dp[i][j] == dp[i - 1][j - w[i]] + v[i]) {
item[i] = 1;
findWhat(i - 1, j - w[i]);
}
}
- 回溯法
回溯法的原理:首先需要构造解的子集树。对于每一个物品i,对于该物品只有选与不选2个决策,总共有n个物品,可以顺序依次考虑每个物品,这样就形成了一棵解空间树:基本思想就是遍历这棵树,以枚举所有情况,最后进行判断,如果重量不超过背包最大承重,且价值最大的话,该方案就是最后的答案。
在搜索状态空间树时,只要左子节点是可一个可行结点,搜索就进入其左子树。对于右子树时,先计算上界函数,以判断是否将其减去(剪枝)。
例如:对于n=4的0/1背包问题,其解空间树如图所示,树中的16个叶子结点分别代表该问题的16个可能解。
3-1解空间树图
回溯法的特点在于将对n个物品放或不放的问题转化用空间树求解向量xi的问题
其中, (xi = 0 或1,xi = 0表示物体i不放入背包,xi =1表示把物体i放入背包)。
在递归函数Backtrack中,
当i>n时,算法搜索至叶子结点,得到一个新的物品装包方案。此时算法适时更新当前的最优价值
当i
关键技术代码:
//构造回溯函数
void backtrack(int i)
{ //i用来指示到达的层数(第几步,从0开始),同时也指示当前完成了几个物品的选择。
double bound(int i);
if(i>n) //递归结束的判定条件
{
bestp = cp;
return;
}
//如若左子节点可行,则直接搜索左子树;
//对于右子树,先计算上界函数,以判断是否将其减去
if(cw+w[i]<=c)//将物品i放入背包,搜索左子树
{
cw+=w[i];//同步更新当前背包的重量
cp+=v[i];//同步更新当前背包的总价值
put[i]=1;
backtrack(i+1);//深度搜索进入下一层
cw-=w[i];//回溯复原
cp-=v[i];//回溯复原
}
if(bound(i+1)>bestp)//如若符合条件则搜索右子树
backtrack(i+1);
}
//计算上界函数并剪枝
double bound(int i)
{ //判断当前背包的总价值cp+剩余容量可容纳的最大价值<=当前最优价值
double leftw= c-cw;//剩余背包容量
double b = cp;//记录当前背包的总价值cp,最后求上界
//以物品单位重量价值递减次序装入物品
while(i<=n && w[i]<=leftw)
{
leftw-=w[i];
b+=v[i];
i++;
}
//装满背包
if(i<=n)
b+=v[i]/w[i]*leftw;
return b;//返回计算出的上界
}
回溯法的原理:分支限界法常以广度优先或以最小耗费(最大效益)优先的方式搜索问题的解空间树。
- 分支限界法
分支限界法原理:每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点,就一次性产生其所有儿子结点。在这些儿子结点中,导致不可行解或导致非最优解的儿子结点被舍弃,其余儿子结点被加入活结点表中。
此后,从活结点表中取下一结点成为当前扩展结点,并重复上述结点扩展过程。一直持续到找到所需的解或活结点表为空时为止。
求解思路特点:首先确定一个合理的限界函数,并根据限界函数确定目标函数的界[down, up];然后按照广度优先策略遍历问题的解空间树,在某一分支上,依次搜索该结点的所有孩子结点,分别估算这些孩子结点的目标函数的可能取值(对最小化问题,估算结点的down,对最大化问题,估算结点的up)。如果某孩子结点的目标函数值超出目标函数的界,则将其丢弃(从此结点生成的解不会比目前已得的更好),否则入待处理表。
关键技术代码:
while(true)
{
if(ew+w[i]<=c)//ew、w[i]表示扩展结点对应的载重量
inQueue(ev+v[i],ew+w[i],i);
inQueue(ev,ew,i);
deQueue(loadingQueue, ev,ew);
if(ev==-1) //同层结点尾部
{
if(emptyQueue(loadingQueue))
{
printf("the result is %d.\n",bestvalue);
}
enQueue(loadingQueue,-1,0);
deQueue(loadingQueue, ev,ew);
i++;
}
}
return 0;
- 算法测试
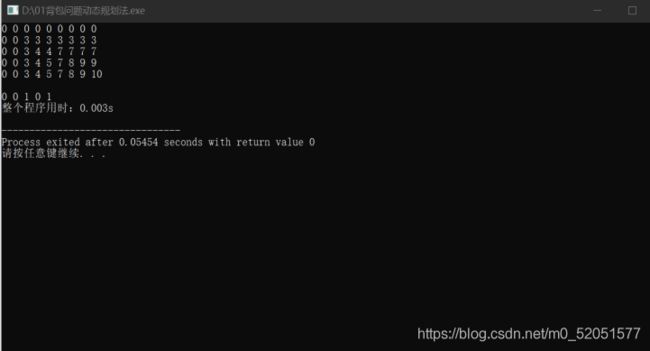
(一)动态规划法测试时间:
4-1动态规划法运行窗
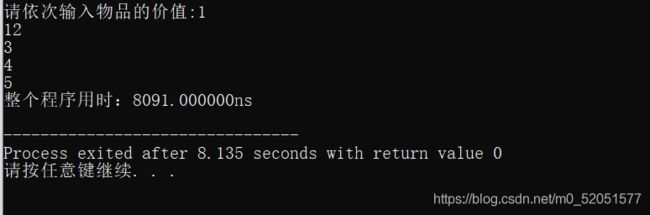
4-2回溯法运行窗
4-3分支限界法运行窗
根据结果可以得出,回溯法的效率是最低的,而动态规划法和分支限界法的效率远高于回溯法。
对于回溯法而言:
因为物品只有选与不选2个决策,而总共有n个物品,所以时间复杂度为。
因为递归栈最多达到n层,而且存储所有物品的信息也只需要常数个一维数组,所以最终的空间复杂度为O(n)。
五、实验体会
本实验我们利用动态规划法、回溯法、分支限界法这三种方法对0-1背包问题进行求解。并通过比较三者代码的执行时间得出分支限界法运行效率最高的结论。
对于完成的项目,还有更好的方案。
回溯法可优化的方法:
剪枝一:可以进行剪枝,因为很多情况是没有意义的,当重量大于背包最大承重时,没有必要再对余下的物品进行决策。
剪枝二:将剩下的所有物品都选取总价值也没有目前已经求得的方案的价值还大的话,也可以返回。
此外,对于动态规划法,选取的数据集是固定的,不能由系统随机分配数据集进行最大价值的计算,因此这是代码需要改进的地方。