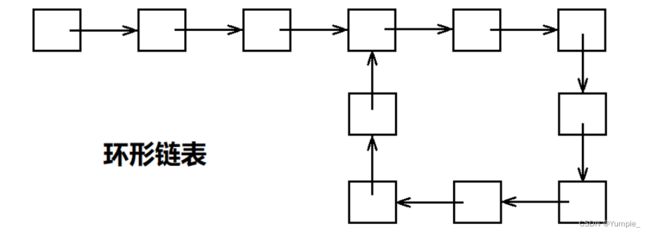
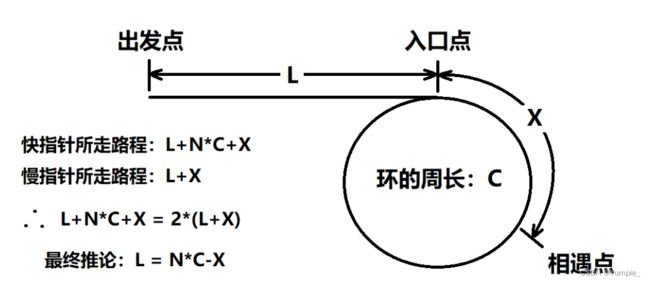
- AI驱动的个人工作革命:基于DeepSeek构建全场景智能工作助理(含源代码+多应用场景)
AI_DL_CODE
DeepSeek深度应用人工智能DeepSeek个人智能助理LangChain任务自动化知识管理大模型应用
摘要:本文详细阐述基于DeepSeek大模型构建个人工作助理的完整技术方案,通过LangChain实现任务分解、知识检索与工具调用的智能协同。方案融合向量数据库、多模态交互与个性化学习算法,构建涵盖邮件处理、会议管理、文档生成等15大核心工作场景的自动化系统。文中提供可运行代码、完整部署指南及效能测试数据,实现邮件处理效率提升13倍、会议纪要生成时间缩短100%、任务安排错误率降低83%的显著优化
- Python 网络爬虫的基本流程及 robots 协议详解
女码农的重启
python网络爬虫JAVA开发语言
数据驱动的时代,网络爬虫作为高效获取互联网信息的工具,其规范化开发离不开对基本流程的掌握和对robots协议的遵守。本文将系统梳理Python网络爬虫的核心流程,并深入解读robots协议的重要性及实践规范。一、Python网络爬虫的基本流程Python网络爬虫的工作过程可分为四个核心阶段,每个阶段环环相扣,共同构成数据采集的完整链路。1.1发起网络请求这是爬虫与目标服务器交互的第一步,通过发送H
- JVM内存泄漏与内存溢出:原理详解与实战应对策略
一、核心概念深度解析内存问题一直是Java开发者面临的重要挑战,理解内存泄漏和内存溢出的本质区别是解决这类问题的第一步。1.1内存泄漏(MemoryLeak)定义:当应用程序不再需要某些对象时,由于仍然存在对这些对象的引用,导致垃圾收集器(GC)无法回收这些内存空间。关键特征:渐进式发展,如同慢性病通常由编码缺陷引起最终可能导致内存溢出1.2内存溢出(OutOfMemoryError)定义:是内存
- python中的pydantic是什么?
John Song
Pythonpython前端开发语言pydantic
Pydantic是Python中一个用于数据验证和设置管理的库,主要通过Python类型注解(TypeHints)来定义数据结构,并自动验证输入数据的合法性。它广泛应用于API开发(如FastAPI)、配置管理、数据序列化等场景。核心功能数据验证自动检查输入数据是否符合类型和约束条件(如字符串长度、数字范围等)。类型转换将原始数据(如JSON、字典)转换为Python类型(如datetime、En
- JSZip 使用详解
啃火龙果的兔子
开发DEMO前端javascript
JSZip使用详解JSZip是一个用于创建、读取和编辑ZIP文件的JavaScript库,完全在浏览器中运行,也支持Node.js环境。安装浏览器环境Node.js环境npminstalljszip#或yarnaddjszip基本使用1.创建一个ZIP文件constJSZip=require("jszip");//Node.js中需要constzip=newJSZip();//添加文本文件zip.
- Mammoth.js 使用详解
啃火龙果的兔子
开发DEMO前端javascript
Mammoth.js使用详解Mammoth.js是一个用于将Word文档(.docx)转换为HTML或Markdown的JavaScript库,支持浏览器和Node.js环境。安装浏览器环境Node.js环境npminstallmammoth#或yarnaddmammoth基本使用1.将DOCX转换为HTML//浏览器中使用input[type=file]获取文件document.getEleme
- 异物检测的计算机视觉算法技术路线
思绪漂移
计算机视觉算法人工智能
异物检测的计算机视觉算法技术路线在现代智能监测系统中,异物检测有着其必要性和运维重要性,通过计算机视觉算法,可以实时识别各种异常物体,为设备安全运行提供有力保障。本文将介绍异物检测的主要技术路线。一、分类识别适应场景分类识别技术主要适用于已知目标类别的异物检测场景。在运维环境中,这类场景包括:固定区域内的障碍物监测(如轨道区域的石块、工具、动物等)关键部件的异物附着检测(如固定装置上的杂物)安全通
- 代码整洁之道:在 Vue 项目中使用 ESLint 的最佳实践
乐闻x
Vue进阶笔记手册前端知识图谱vue.js前端javascript
系列文章ESLint使用教程(一):从零配置ESLintESLint使用教程(二):一步步教你编写Eslint自定义规则ESLint使用教程(三):12个ESLint配置项功能与使用方式详解ESLint使用教程(四):ESLint有哪些执行时机?ESLint使用教程(五):ESLint和Prettier的结合使用与冲突解决ESLint使用教程(六):从输入eslint命令到最终代码被处理,ESLi
- 前端自动化测试最佳实践:Jest与Cypress详解
目录前言自动化测试概述Jest详解Jest基础配置单元测试实践组件测试Mock与Stub快照测试Cypress详解Cypress环境搭建端到端测试实践页面交互测试API模拟测试策略与最佳实践测试金字塔测试覆盖率持续集成常见问题与解决方案总结前言随着前端应用的复杂度不断提高,确保代码质量和稳定性变得越来越重要。自动化测试作为保障代码质量的重要手段,已成为现代前端开发流程中不可或缺的一环。本文将详细介
- PageRank:互联网的马尔可夫链平衡态
大千AI助手
人工智能Python#OTHER人工智能机器学习条件概率贝叶斯PageRank马尔科夫链MC
本文由「大千AI助手」原创发布,专注用真话讲AI,回归技术本质。拒绝神话或妖魔化。搜索「大千AI助手」关注我,一起撕掉过度包装,学习真实的AI技术!PageRank算法本质上是一个在网页图上定义的离散时间马尔可夫链(DTMC),其核心思想是将网页间的链接关系转化为状态转移概率。以下是详细分析:一、马尔可夫链的核心要素在PageRank中的体现马尔可夫链要素PageRank对应数学描述状态空间网页集
- MCMC:高维概率采样的“随机游走”艺术
大千AI助手
人工智能Python#OTHER人工智能数据挖掘机器学习算法MCMC马尔科夫概率论
MCMC(马尔可夫链蒙特卡洛)是一种从复杂概率分布中高效采样的核心算法,它解决了传统采样方法在高维空间中的“维度灾难”问题。以下是其技术本质、关键算法及实践的深度解析:本文由「大千AI助手」原创发布,专注用真话讲AI,回归技术本质。拒绝神话或妖魔化。搜索「大千AI助手」关注我,一起撕掉过度包装,学习真实的AI技术!一、MCMC要解决的核心问题目标:从目标分布(π(x)\pi(\mathbf{x})
- LeetCode 刷题:数据结构与算法的实战经验分享
LeetCode刷题:数据结构与算法的实战经验分享关键词:LeetCode、数据结构、算法、刷题经验、实战摘要:本文将围绕LeetCode刷题展开,深入探讨数据结构与算法在实际刷题过程中的应用。通过分享实战经验,帮助读者更好地理解和掌握数据结构与算法知识,提升解题能力。文章将从背景介绍入手,阐述刷题的目的和意义,接着详细解释核心概念,分析它们之间的关系,然后介绍核心算法原理和具体操作步骤,结合数学
- 高压电缆护层电流监测系统的技术实现
李子圆圆
人工智能
目录文章目录概要高精度电流监测的技术实现多级预警机制的构建逻辑极端环境下的稳定运行技术远程运维的技术支撑概要高压电缆护层作为电力传输的关键防护结构,其接地电流的异常变化是判断设备状态的重要指标。TLKS-PLGD高压电缆护层电流监测系统通过传感器技术与智能算法的结合,构建了一套完整的电缆安全监测方案。高精度电流监测的技术实现高精度电流监测的技术实现护层电流监测的核心在于数据采集的精准性。该系统采用
- 网络安全-反弹shell详解(攻击,检测与防御)
程序员鱼
web安全网络安全单片机服务器linuxuni-app
反弹Shell:详解、攻击、检测与防御反弹Shell(ReverseShell)是一种网络安全领域中常见的攻击技术,通常用于远程控制受害者的计算机。本文旨在从网络安全的角度详细介绍反弹Shell的工作原理,实施方法以及如何检测和防御这类攻击。一、Shell的简介与原理1.1什么是Shell?Shell在计算机系统中指的是一个用户界面,用于访问操作系统的服务。在网络安全中,攻击者常利用Shell来控
- 构建安全密码存储策略:核心原则与最佳实践
weixin_47233946
信息安全安全
密码是用户身份认证的第一道防线,其存储安全性直接关系到用户隐私和企业信誉。近年来频发的数据泄露事件揭示了密码管理的关键性。本文将深入探讨从加密算法到系统性防护的完整密码存储方案,帮助开发者构建企业级安全防御体系。一、密码存储基本准则绝对禁止明文存储:即使采用数据库加密措施,直接存储用户原始密码仍存在不可逆泄露风险。运维人员权限滥用或备份文件泄露都可能成为突破口。加密≠安全:AES等对称加密存在密钥
- 数据结构实验解析(C++版)——实验一 复杂度分析
拯救三金
数据结构c++算法
目录一、实验例题例题1例题2二、实验原理与背景知识1、实验原理2、背景知识三、解题思路与算法1、解题思路2、算法四、代码实现例题1代码例题2代码五、实验结果分析与总结1、实验结果分析2、该实验与数据结构的联系一、实验例题例题1时间空间限制时间限制:1SEC空间限制:128MB问题描述分析以下代码:for(i=1;iusingnamespacestd;intmain(){longlongn;//输入
- Spring Data Neo4j 与后端人工智能算法的数据交互
AI大模型应用实战
springneo4j人工智能ai
SpringDataNeo4j与后端人工智能算法的数据交互关键词:SpringDataNeo4j、图数据库、人工智能算法、数据交互、知识图谱、图神经网络、数据集成摘要:本文深入探讨了如何利用SpringDataNeo4j框架实现后端人工智能算法与图数据库的高效数据交互。文章首先介绍了图数据库和人工智能算法的基本概念,然后详细解析了SpringDataNeo4j的核心架构和原理。接着,通过实际代码示
- 【HCIA】TCP三次握手、4次断开详解
戏精亿点点菜
tcp/ip网络服务器
TCP(传输控制协议)是一种面向连接的、可靠的、基于字节流的传输层通信协议。在TCP/IP协议族中,TCP负责在两个网络实体之间建立、维护和终止连接。TCP连接的建立和终止分别通过三次握手和四次断开来完成。一、三次挥手TCP三次握手是建立TCP连接的过程,它确保了通信双方都准备好进行数据传输。过程如下:客户端->服务器:SYN,ISN=x服务器->客户端:SYN,ACK,ISN=y,ACK(x+1
- 【数据结构】复杂度分析
目录一、算法1.基本概念2.描述方法3.算法效率二、算法的时间复杂度三、算法的空间复杂度一、算法1.基本概念通俗的讲,算法是解决问题的方法,比如在现实生活中一道菜谱,一个安装轮椅的操作指南等。严格的说,算法是对特定问题求解步骤的一种描述,是指令的有限序列。算法具有的基本特性有:(1)有穷性。一个算法必须总是在执行有穷步之后结束,且每一步都在有求时间内完成。(2)确定性。算法中的每一条指令必须有确切
- C语言指针进阶完全指南:从多级指针到函数指针的深度探索
给老吕螺丝
#C语言c语言开发语言
掌握指针基础后,你将开启C语言真正的力量之门。本文通过实战代码示例和内存布局图解,带你系统攻克指针进阶技术。一、指针核心回顾与进阶重点核心概念:指针本质:存储内存地址的变量间接访问:通过地址操作数据指针大小:64位系统固定8字节(与类型无关)进阶重点:多级指针:处理复杂间接关系动态内存管理:精准控制内存生命周期函数指针:实现代码抽象与回调复杂结构:构建链表等动态数据结构二、多级指针:指针的指针内存
- 视觉算法之卷积神经网络
清风AI
深度学习算法详解及代码复现计算机视觉cnn神经网络深度学习python课程设计毕业设计
定义与特点卷积神经网络(ConvolutionalNeuralNetwork,CNN)是一种专为处理具有网格结构的数据而设计的深度学习模型。其独特的结构和功能使其在图像处理、语音识别等领域展现出卓越的性能:CNN的核心设计理念源于对生物视觉系统的模仿。通过模拟大脑皮层中视网膜和视觉皮层的层次化结构,CNN能够有效地捕捉图像中的局部特征并逐步抽象为高层语义信息。这种设计使得CNN特别擅长处理图像和音
- 心理健康语音分析AI模型:开启心理评估新时代
AI大模型应用实战
人工智能语音识别ai
心理健康语音分析AI模型:开启心理评估新时代关键词:心理健康评估、语音信号处理、情感计算、AI模型、多模态融合摘要:传统心理评估依赖量表问卷和人工观察,存在主观性强、效率低、难以实时监测等局限。本文将带您走进“心理健康语音分析AI模型”的世界,从基础概念到核心技术,从算法原理到实战案例,揭秘AI如何通过“听声音”读懂心理状态,开启心理评估的智能化新时代。背景介绍目的和范围心理健康问题已成为全球公共
- MySQL存储结构深度解析:Buffer Pool与Page管理
hdzw20
mysql复习mysql数据库
MySQL存储结构解析:BufferPool与Page管理在MySQL的InnoDB存储引擎中,BufferPool是其核心组件之一,它极大地提升了数据库的性能。理解BufferPool的内部结构和工作机制,对于优化MySQL数据库至关重要。本文将讨论BufferPool的结构、三大链表、改进型LRU算法以及ChangeBuffer机制。1.BufferPool结构:控制块与缓存页BufferPo
- 【车载测试之CAPL编程系列】:【16】函数定义(2)
车载测试CAPL编程系列:CAPL中的函数定义(2)目录函数定义的基本形式参数类型与返回值函数重载(Overload)返回值限制:不能返回数组AI总结函数定义的基本形式CAPL函数定义具有灵活性,可根据需求设计无返回值、无参数的函数。无返回值、无参数的函数返回值类型:若函数无返回值,可声明为void,且void关键字可省略(CAPL特性,区别于C语言)。参数:允许无参数,但必须保留空括号()。示例
- 一文详解:使用HTTPS有哪些优势?
JoySSL303
https网络协议httpssl网络
互联网发展到今天,HTTP协议的明文传输会让用户存在非常大的安全隐患。试想一下,假如你在一个HTTP协议的网站上面购物,你需要在页面上输入你的银行卡号和密码,然后你把数据提交到服务器实现购买。假如这个环节稍有不慎,你的传输数据被第三者给截获了,由于HTTP明文数据传输的原因,你的银行卡号和密码,将会被这个截获人所得到。现在你还敢在一个HTTP的网站上面购物吗?你还会在一个HTTP的网站上面留下你的
- Python协程从入门到精通:9个案例解析yield、gevent与asyncio实战
python_chai
Pythonpython开发语言协程并发yield生成器gerrnletgevent
引言痛点分析:传统多线程在高并发场景下的性能瓶颈。协程优势:轻量级、高并发、低资源消耗。本文目标:通过9个代码案例,系统讲解协程的核心技术和应用场景。目录引言1.协程基础:理解yield生成器1.1yield的暂停与恢复机制1.2生产者-消费者模型实战1.3双向通信:send()方法详解2.手动协程控制:greenlet进阶2.1greenlet的显式切换原理2.2多任务协作案例3.自动化协程:g
- 数据结构:位图
顾小玙
数据结构算法
目录问题引入位图定义相关整型位操作疑点位运算C++库里的bitset实现应用优缺点问题引入有一道经典的面试题:有40亿个无序无符号整数,要求你高效判断一个数是否在这堆数中。想法一:暴力查找似乎能够解决问题,但显然找一次就要消耗O(N)的时间,这是不能接受的;想法二:问题的本质是查找,因此想到使用高效的二分查找:先进行一次O(NlogN)的排序,之后的每次查找都只要O(logN)。想法二的改进很不错
- 多模态大模型发展全景:从架构创新到应用突破
陈敬雷-充电了么-CEO兼CTO
python大模型多模态大模型AIGC机器学习深度学习DeepSeek
注:此文章内容均节选自充电了么创始人,CEO兼CTO陈敬雷老师的新书《GPT多模态大模型与AIAgent智能体》(跟我一起学人工智能)【陈敬雷编著】【清华大学出版社】《GPT多模态大模型与AIAgent智能体》新出书籍配套视频【陈敬雷】推荐算法系统实战全系列精品课【陈敬雷】文章目录GPT多模态大模型系列四多模态大模型发展全景:从架构创新到应用突破更多技术内容总结GPT多模态大模型系列四多模态大模型
- c语言逻辑运算符编程,C语言之逻辑运算符详解
湛蓝色的迷惘
c语言逻辑运算符编程
一逻辑运算符:&&:逻辑与,读作并且表达式左右两边都为真,那么结果才为真口诀:一假则假||:逻辑或,读作或者表达式左右两边,有一个为真,那么结果就为真口诀:一真则真!:逻辑非,读作取反表达式的结果如果为假,就变成真,如果为真,就变成假口诀:真变假,假变真二逻辑运算符的短路问题tips:非0为真,0为假短路的情况:&&:左边如果为假,则右边短路(右边不会被执行)||:左边如果为真,则右边短路(右边不
- C语言正则表达式使用详解
标准的C和C++都不支持正则表达式,但有正则表达式的函数库提供这功能.C语言处理正则表达式常用的函数有regcomp()、regexec()、regfree()和regerror()。使用正则表达式步骤:1)编译正则表达式regcomp()2)匹配正则表达式regexec()3)释放正则表达式regfree()4)获取regcomp或者regexec产生错误,获取包含错误信息的字符串函数声明如下:
- sql统计相同项个数并按名次显示
朱辉辉33
javaoracle
现在有如下这样一个表:
A表
ID Name time
------------------------------
0001 aaa 2006-11-18
0002 ccc 2006-11-18
0003 eee 2006-11-18
0004 aaa 2006-11-18
0005 eee 2006-11-18
0004 aaa 2006-11-18
0002 ccc 20
- Android+Jquery Mobile学习系列-目录
白糖_
JQuery Mobile
最近在研究学习基于Android的移动应用开发,准备给家里人做一个应用程序用用。向公司手机移动团队咨询了下,觉得使用Android的WebView上手最快,因为WebView等于是一个内置浏览器,可以基于html页面开发,不用去学习Android自带的七七八八的控件。然后加上Jquery mobile的样式渲染和事件等,就能非常方便的做动态应用了。
从现在起,往后一段时间,我打算
- 如何给线程池命名
daysinsun
线程池
在系统运行后,在线程快照里总是看到线程池的名字为pool-xx,这样导致很不好定位,怎么给线程池一个有意义的名字呢。参照ThreadPoolExecutor类的ThreadFactory,自己实现ThreadFactory接口,重写newThread方法即可。参考代码如下:
public class Named
- IE 中"HTML Parsing Error:Unable to modify the parent container element before the
周凡杨
html解析errorreadyState
错误: IE 中"HTML Parsing Error:Unable to modify the parent container element before the child element is closed"
现象: 同事之间几个IE 测试情况下,有的报这个错,有的不报。经查询资料后,可归纳以下原因。
- java上传
g21121
java
我们在做web项目中通常会遇到上传文件的情况,用struts等框架的会直接用的自带的标签和组件,今天说的是利用servlet来完成上传。
我们这里利用到commons-fileupload组件,相关jar包可以取apache官网下载:http://commons.apache.org/
下面是servlet的代码:
//定义一个磁盘文件工厂
DiskFileItemFactory fact
- SpringMVC配置学习
510888780
springmvc
spring MVC配置详解
现在主流的Web MVC框架除了Struts这个主力 外,其次就是Spring MVC了,因此这也是作为一名程序员需要掌握的主流框架,框架选择多了,应对多变的需求和业务时,可实行的方案自然就多了。不过要想灵活运用Spring MVC来应对大多数的Web开发,就必须要掌握它的配置及原理。
一、Spring MVC环境搭建:(Spring 2.5.6 + Hi
- spring mvc-jfreeChart 柱图(1)
布衣凌宇
jfreechart
第一步:下载jfreeChart包,注意是jfreeChart文件lib目录下的,jcommon-1.0.23.jar和jfreechart-1.0.19.jar两个包即可;
第二步:配置web.xml;
web.xml代码如下
<servlet>
<servlet-name>jfreechart</servlet-nam
- 我的spring学习笔记13-容器扩展点之PropertyPlaceholderConfigurer
aijuans
Spring3
PropertyPlaceholderConfigurer是个bean工厂后置处理器的实现,也就是BeanFactoryPostProcessor接口的一个实现。关于BeanFactoryPostProcessor和BeanPostProcessor类似。我会在其他地方介绍。PropertyPlaceholderConfigurer可以将上下文(配置文件)中的属性值放在另一个单独的标准java P
- java 线程池使用 Runnable&Callable&Future
antlove
javathreadRunnablecallablefuture
1. 创建线程池
ExecutorService executorService = Executors.newCachedThreadPool();
2. 执行一次线程,调用Runnable接口实现
Future<?> future = executorService.submit(new DefaultRunnable());
System.out.prin
- XML语法元素结构的总结
百合不是茶
xml树结构
1.XML介绍1969年 gml (主要目的是要在不同的机器进行通信的数据规范)1985年 sgml standard generralized markup language1993年 html(www网)1998年 xml extensible markup language
- 改变eclipse编码格式
bijian1013
eclipse编码格式
1.改变整个工作空间的编码格式
改变整个工作空间的编码格式,这样以后新建的文件也是新设置的编码格式。
Eclipse->window->preferences->General->workspace-
- javascript中return的设计缺陷
bijian1013
JavaScriptAngularJS
代码1:
<script>
var gisService = (function(window)
{
return
{
name:function ()
{
alert(1);
}
};
})(this);
gisService.name();
&l
- 【持久化框架MyBatis3八】Spring集成MyBatis3
bit1129
Mybatis3
pom.xml配置
Maven的pom中主要包括:
MyBatis
MyBatis-Spring
Spring
MySQL-Connector-Java
Druid
applicationContext.xml配置
<?xml version="1.0" encoding="UTF-8"?>
&
- java web项目启动时自动加载自定义properties文件
bitray
javaWeb监听器相对路径
创建一个类
public class ContextInitListener implements ServletContextListener
使得该类成为一个监听器。用于监听整个容器生命周期的,主要是初始化和销毁的。
类创建后要在web.xml配置文件中增加一个简单的监听器配置,即刚才我们定义的类。
<listener>
<des
- 用nginx区分文件大小做出不同响应
ronin47
昨晚和前21v的同事聊天,说到我离职后一些技术上的更新。其中有个给某大客户(游戏下载类)的特殊需求设计,因为文件大小差距很大——估计是大版本和补丁的区别——又走的是同一个域名,而squid在响应比较大的文件时,尤其是初次下载的时候,性能比较差,所以拆成两组服务器,squid服务于较小的文件,通过pull方式从peer层获取,nginx服务于较大的文件,通过push方式由peer层分发同步。外部发布
- java-67-扑克牌的顺子.从扑克牌中随机抽5张牌,判断是不是一个顺子,即这5张牌是不是连续的.2-10为数字本身,A为1,J为11,Q为12,K为13,而大
bylijinnan
java
package com.ljn.base;
import java.util.Arrays;
import java.util.Random;
public class ContinuousPoker {
/**
* Q67 扑克牌的顺子 从扑克牌中随机抽5张牌,判断是不是一个顺子,即这5张牌是不是连续的。
* 2-10为数字本身,A为1,J为1
- 翟鸿燊老师语录
ccii
翟鸿燊
一、国学应用智慧TAT之亮剑精神A
1. 角色就是人格
就像你一回家的时候,你一进屋里面,你已经是儿子,是姑娘啦,给老爸老妈倒怀水吧,你还觉得你是老总呢?还拿派呢?就像今天一样,你们往这儿一坐,你们之间是什么,同学,是朋友。
还有下属最忌讳的就是领导向他询问情况的时候,什么我不知道,我不清楚,该你知道的你凭什么不知道
- [光速与宇宙]进行光速飞行的一些问题
comsci
问题
在人类整体进入宇宙时代,即将开展深空宇宙探索之前,我有几个猜想想告诉大家
仅仅是猜想。。。未经官方证实
1:要在宇宙中进行光速飞行,必须首先获得宇宙中的航行通行证,而这个航行通行证并不是我们平常认为的那种带钢印的证书,是什么呢? 下面我来告诉
- oracle undo解析
cwqcwqmax9
oracle
oracle undo解析2012-09-24 09:02:01 我来说两句 作者:虫师收藏 我要投稿
Undo是干嘛用的? &nb
- java中各种集合的详细介绍
dashuaifu
java集合
一,java中各种集合的关系图 Collection 接口的接口 对象的集合 ├ List 子接口 &n
- 卸载windows服务的方法
dcj3sjt126com
windowsservice
卸载Windows服务的方法
在Windows中,有一类程序称为服务,在操作系统内核加载完成后就开始加载。这里程序往往运行在操作系统的底层,因此资源占用比较大、执行效率比较高,比较有代表性的就是杀毒软件。但是一旦因为特殊原因不能正确卸载这些程序了,其加载在Windows内的服务就不容易删除了。即便是删除注册表中的相 应项目,虽然不启动了,但是系统中仍然存在此项服务,只是没有加载而已。如果安装其他
- Warning: The Copy Bundle Resources build phase contains this target's Info.plist
dcj3sjt126com
iosxcode
http://developer.apple.com/iphone/library/qa/qa2009/qa1649.html
Excerpt:
You are getting this warning because you probably added your Info.plist file to your Copy Bundle
- 2014之C++学习笔记(一)
Etwo
C++EtwoEtwoiterator迭代器
已经有很长一段时间没有写博客了,可能大家已经淡忘了Etwo这个人的存在,这一年多以来,本人从事了AS的相关开发工作,但最近一段时间,AS在天朝的没落,相信有很多码农也都清楚,现在的页游基本上达到饱和,手机上的游戏基本被unity3D与cocos占据,AS基本没有容身之处。so。。。最近我并不打算直接转型
- js跨越获取数据问题记录
haifengwuch
jsonpjsonAjax
js的跨越问题,普通的ajax无法获取服务器返回的值。
第一种解决方案,通过getson,后台配合方式,实现。
Java后台代码:
protected void doPost(HttpServletRequest req, HttpServletResponse resp)
throws ServletException, IOException {
String ca
- 蓝色jQuery导航条
ini
JavaScripthtmljqueryWebhtml5
效果体验:http://keleyi.com/keleyi/phtml/jqtexiao/39.htmHTML文件代码:
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<title>jQuery鼠标悬停上下滑动导航条 - 柯乐义<
- linux部署jdk,tomcat,mysql
kerryg
jdktomcatlinuxmysql
1、安装java环境jdk:
一般系统都会默认自带的JDK,但是不太好用,都会卸载了,然后重新安装。
1.1)、卸载:
(rpm -qa :查询已经安装哪些软件包;
rmp -q 软件包:查询指定包是否已
- DOMContentLoaded VS onload VS onreadystatechange
mutongwu
jqueryjs
1. DOMContentLoaded 在页面html、script、style加载完毕即可触发,无需等待所有资源(image/iframe)加载完毕。(IE9+)
2. onload是最早支持的事件,要求所有资源加载完毕触发。
3. onreadystatechange 开始在IE引入,后来其它浏览器也有一定的实现。涉及以下 document , applet, embed, fra
- sql批量插入数据
qifeifei
批量插入
hi,
自己在做工程的时候,遇到批量插入数据的数据修复场景。我的思路是在插入前准备一个临时表,临时表的整理就看当时的选择条件了,临时表就是要插入的数据集,最后再批量插入到数据库中。
WITH tempT AS (
SELECT
item_id AS combo_id,
item_id,
now() AS create_date
FROM
a
- log4j打印日志文件 如何实现相对路径到 项目工程下
thinkfreer
Weblog4j应用服务器日志
最近为了实现统计一个网站的访问量,记录用户的登录信息,以方便站长实时了解自己网站的访问情况,选择了Apache 的log4j,但是在选择相对路径那块 卡主了,X度了好多方法(其实大多都是一样的内用,还一个字都不差的),都没有能解决问题,无奈搞了2天终于解决了,与大家分享一下
需求:
用户登录该网站时,把用户的登录名,ip,时间。统计到一个txt文档里,以方便其他系统调用此txt。项目名
- linux下mysql-5.6.23.tar.gz安装与配置
笑我痴狂
mysqllinuxunix
1.卸载系统默认的mysql
[root@localhost ~]# rpm -qa | grep mysql
mysql-libs-5.1.66-2.el6_3.x86_64
mysql-devel-5.1.66-2.el6_3.x86_64
mysql-5.1.66-2.el6_3.x86_64
[root@localhost ~]# rpm -e mysql-libs-5.1