全文链接:http://tecdat.cn/?p=31733
最近我们被客户要求撰写关于Copula的研究报告,包括一些图形和统计输出。
Copula方法是测度金融市场间尾部相关性比较有效的方法,而且可用于研究非正态、非线性以及尾部非对称等较复杂的相依特征关系
因此,Copula方法开始逐渐代替多元GARCH模型的相关性分析,成为考察金融变量间关系的流行方法,被广泛地用于市场一体化、风险管理以及期货套期保值的研究中。
国内外学者对于尾部相关性和Copula方法已经有了深入的研究,提出多种Copula模型来不断优化尾部相关系数对于不同情况下股票之间相关性的刻画,对于股票的聚类方法也进行了改进和拓展,然而能够结合这些方法对于资产选择进行研究的较少。尤其是在面对现今股票市场海量级的股票数据,如何从股票间的尾部相关性挖掘到有效信息,得到能够有效规避风险的资产组合是很少有人研究的问题。并且大多尾部相关的分析都只停留在定性的分析中,并且多是在市场与市场之间,板块与板块之间的相关性分析,对于股票间定量的相关性研究还有不足。相信研究成果对于投资者有效的规避风险,寻求最佳的投资组合有较大的帮助。
本文结合Copula方法和聚类思想对大数量级的股票间尾部相关性进行分析,帮助客户构建混合Copula模型并计算股票间尾部相关系数,再根据尾部相关系数选用合理高效的聚类方法进行聚类,为投资者选择投资组合提供有效的建议。
上证A股数据
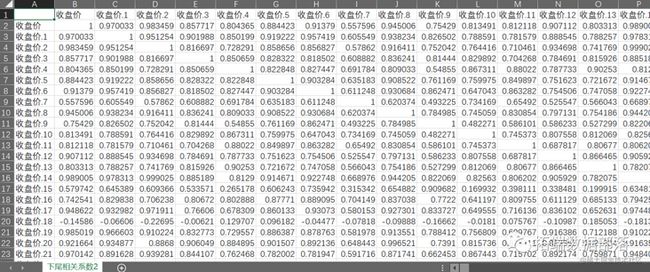
本文选取上证A股数据 ( 查看文末了解数据免费获取方式 ) ,其数据来源于wind数据库。由于时间间隔较长,本文将通过对相关系数进行计算来分析其之间的相关性,然后再通过聚类分析将其合并来进行研究。具体步骤如下:
非参数核估计边缘分布
j=1077
aj=median(sy(:,j)); %(j=1(SZGY),2(SZSY),3(SZDC),4(GYSY))
bj=median(abs(sy(:,j)-aj))/0.6745;
hj=1.06*bj*1077^(-1/5);
1,固定函数的参数,选择权重的初值为:1/ 3。对权重进行估计。
d=cdf('Normal',(sy(n,j)-wj(i))/hj,0,1);
sum=sum+d;
end
2,固定权重为第 1 步的估计值,选择参数的初值为第上一节的估计值,对函数的参数进行估计。
%求似然值
%fenbu=xlsread('fenbu.xlsx'); %读取数据,
fenbu=sy;
u=mean(sy);
3,将第 2 步估计得到的参数值作为固定值,权重初值选择第 1 步的估计值,进行权重估计。
s(j)=s(j)+b(i); %求似然值
end
end
估计混合 Copula 权重
theta=0.5;
for j=1:1000;
k1(1)=0.2; %权重初值
k2(1)=0.3 ;
c3(i)=1077^(-1)*k3(j)*fr(i)*(k1(j)*gu(i)+k2(j)*cl(i)+k3(j)*fr(i))^(-1);
k1(j+1)=k1(j+1)+c1(i); %gu(i),cl(i),fr(i)表示三个函数的密度函数
abs(k3(j+1)-k3(j))<=0.000001); %满足收敛条件是跳出
end
l=length(k1') %收敛时的步骤数目
k1(l),k2(l),k3(l) %收敛时的结果
估计混合 Copula 模型的函数参数
%b=b(0); %参数初值
for j=1:1000; %运算步骤
h1(i)=k1*gu_p(i)*gu(i)/(gu_m(i)*(k1*gu(i)+k2*cl(i)+k3*fr(i)));
s1=s1+h1(i); %gu_p 是 Gumbel 密度函数,gu_m 是 Gumbel 的密度函数
n=13;d=array(0 dim=c(13 13))
for(i in 1:(n-1)){
d[i i]=1
for(j in (i+1):n){
clayton.cop=claytonCopula(3 dim=2);clayton.cop
u=pobs(b);u
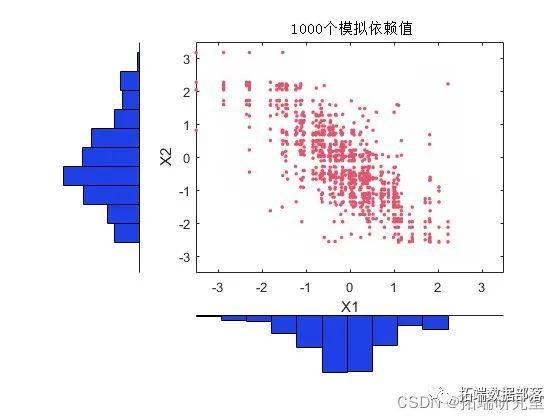
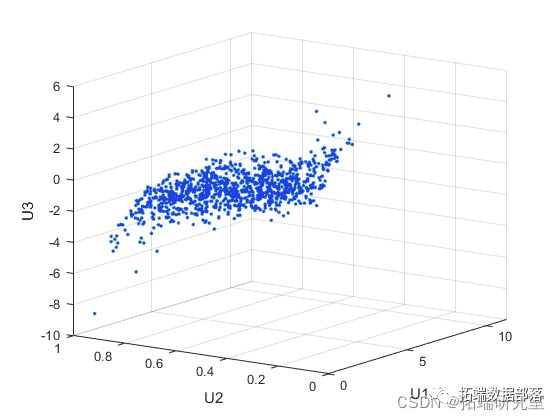
生成随机数
M=0.247060*G'+0.441831*C'+0.311109*F'; %生成混合 Copula 随机数计算每个不同类时的 k-means 聚类结果,并计算平均偏差,且画出图形
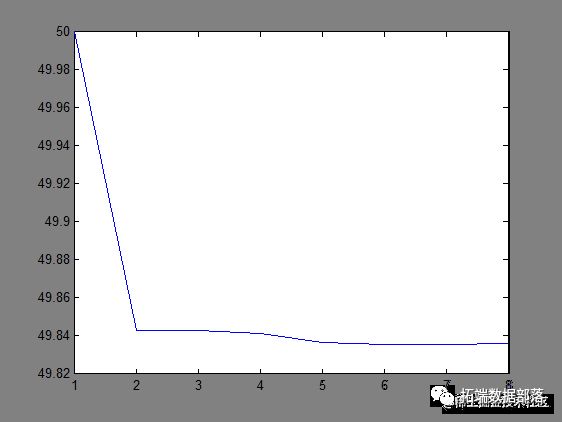
for c = 2:8
[idx,ctrs] = kmeans(M,c);
点击标题查阅往期内容
用COPULA模型进行蒙特卡洛(MONTE CARLO)模拟和拟合股票收益数据分析
左右滑动查看更多
01
02
03
04
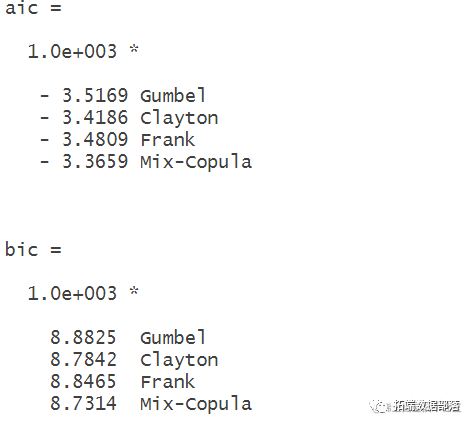
[aic,bic] = aicbic([logL1;logL2;logL3;logL4],
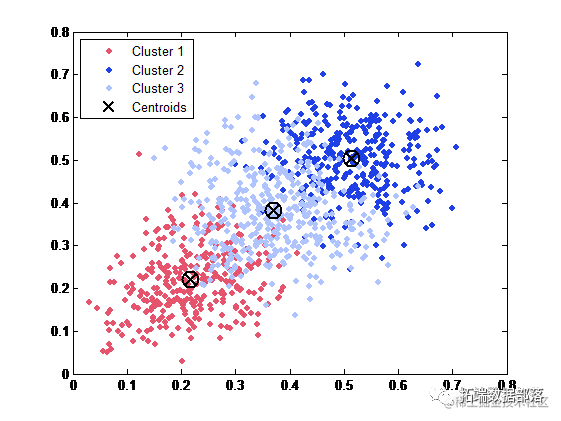
当聚类数目为 7 时的 k-means 聚类
c=7;
[idx,ctrs] = kmeans(M,c);
X=M
plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12)
上尾
hold on
plot(X(idx==4,1),X(idx==4,2),'b.','MarkerSize',12)
hold on
plot(X(idx==5,1),X(idx==5,2),'b.','MarkerSize',12)
hold on
plot(X(idx==6,1),X(idx==6,2),'b.','MarkerSize',12)
hold on
plot(X(idx==7,1),X(idx==7,2),'b.','MarkerSize',12)
hold on
plot(X(idx==8,1),X(idx==8,2),'b.','MarkerSize',12)
hold on
plot(ctrs(:,1),ctrs(:,2),'kx',...
Average square within cluster
library(cluster)
agn1=aes(delta method="average");agn1
plot(x with.ss")
lines(x with.ss lty=2)
下尾
Average square within cluster
输出上尾和下尾相关系数
本文将 Copula方法应用到股票市场的相关分析中,以上证A股数据作为研究对象,基于 Copula方法构建了对不同投资组合的风险和收益的预测模型;其次,将聚类思想应用到股票选择中,将选择出来的股票进行聚类分析,得出各个聚类结果。本文不仅考虑了股票之间的相关关系,还考虑了它们之间的相关性。
输出股票类别
数据获取
在公众号后台回复“a股数****据”,可免费获取完整数据。
点击文末 “阅读原文”
获取全文完整代码数据资料。
本文选自《MATLAB、R基于Copula方法和k-means聚类的股票选择研究上证A股数据》。
点击标题查阅往期内容
用COPULA模型进行蒙特卡洛(MONTE CARLO)模拟和拟合股票收益数据分析\
Copula 算法建模相依性分析股票收益率时间序列案例\
Copula估计边缘分布模拟收益率计算投资组合风险价值VaR与期望损失ES\
MATLAB用COPULA模型进行蒙特卡洛(MONTE CARLO)模拟和拟合股票收益数据分析\
R语言多元Copula GARCH 模型时间序列预测\
python中的copula:Frank、Clayton和Gumbel copula模型估计与可视化\
R语言中的copula GARCH模型拟合时间序列并模拟分析\
matlab使用Copula仿真优化市场风险数据VaR分析\
R语言多元Copula GARCH 模型时间序列预测\
R语言Copula函数股市相关性建模:模拟Random Walk(随机游走)\
R语言实现 Copula 算法建模依赖性案例分析报告\
R语言ARMA-GARCH-COPULA模型和金融时间序列案例\
R语言基于copula的贝叶斯分层混合模型的诊断准确性研究\
R语言COPULA和金融时间序列案例\
matlab使用Copula仿真优化市场风险数据VaR分析\
matlab使用Copula仿真优化市场风险\
R语言多元CopulaGARCH模型时间序列预测\
R语言Copula的贝叶斯非参数MCMC估计\
R语言COPULAS和金融时间序列R语言乘法GARCH模型对高频交易数据进行波动性预测\
R语言GARCH-DCC模型和DCC(MVT)建模估计\
Python使用GARCH,EGARCH,GJR-GARCH模型和蒙特卡洛模拟进行股价预测\
R语言时间序列GARCH模型分析股市波动率\
R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测\
matlab实现MCMC的马尔可夫转换ARMA - GARCH模型估计\
Python使用GARCH,EGARCH,GJR-GARCH模型和蒙特卡洛模拟进行股价预测\
使用R语言对S&P500股票指数进行ARIMA + GARCH交易策略\
R语言用多元ARMA,GARCH ,EWMA, ETS,随机波动率SV模型对金融时间序列数据建模\
R语言股票市场指数:ARMA-GARCH模型和对数收益率数据探索性分析\
R语言多元Copula GARCH 模型时间序列预测\
R语言使用多元AR-GARCH模型衡量市场风险\
R语言中的时间序列分析模型:ARIMA-ARCH / GARCH模型分析股票价格\
R语言用Garch模型和回归模型对股票价格分析\
GARCH(1,1),MA以及历史模拟法的VaR比较\
matlab估计arma garch 条件均值和方差模型\
R语言ARMA-GARCH-COPULA模型和金融时间序列案例