【数据结构】栈和队列
[数据结构]栈和队列
文章目录
- [数据结构]栈和队列
- 一. 栈
-
- 1.了解栈
- 2.顺序栈
-
- 1.顺序栈的定义
- 2.初始化
- 3.判空&判满
- 4.入栈
- 5.出栈
- 6.顺序栈的完整实现
- 3.共享栈
-
- 1.共享栈的定义
- 2.初始化
- 3.判空&判满
- 4.入栈
- 5.出栈
- 6.共享栈的完整实现
- 4.链栈
-
- 1.链栈的定义
- 2.初始化
- 3.判空
- 4.入栈
- 5.出栈
- 二. 队列
-
- 1.了解队列
- 2.队列的顺序存储结构
-
- 1.顺序队列的定义
- 2.判空&判满 ?
- 3.循环队列
-
- 1.了解循环队列
- 2. 牺牲单元法
- 3. tag法
- 4. size法
- 4.队列的链式存储结构
-
- 1.链队列的定义
- 2.初始化
- 3.判空
- 4.入队
- 5.出队
- 5.双端队列
-
- 1.了解双端队列
- 2.受限的双端队列
- 3.双端队列的操作
一. 栈
1.了解栈
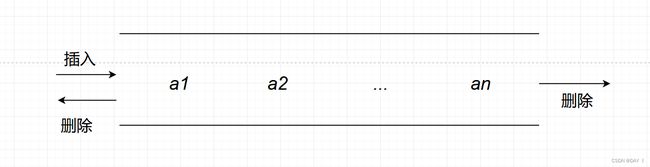
什么是栈?
栈:是只允许在一端进行插入或删除的线性表(是特殊的限制存取点的线性表)
栈的基本性质:
- 栈是一种逻辑结构
- 栈满足后进先出(LIFO)
- 栈的数学性质:
n个不同的元素进栈,出栈元素不同排列的个数为: 1 n + 1 C 2 n n \frac {1} {n + 1}C_{2n}^{n} n+11C2nn
2.顺序栈
1.顺序栈的定义
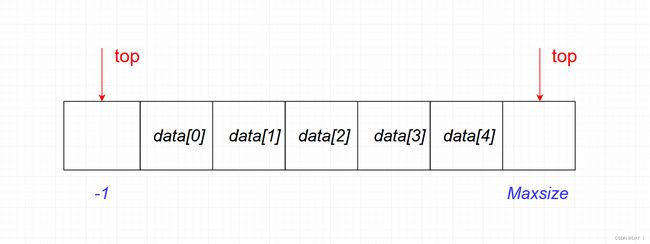
顺序栈:利用顺序存储方式存储的栈,它利用了一组地址连续的存储单元存放自栈底至栈顶的数据元素,同时开辟一片内存空间用于存放栈顶指针 t o p top top(指向栈顶元素的位置)
顺序栈的结构体定义:
#define Maxsize 50
typedef struct Stack {
Elemtype data[Maxsize]; //静态数组存放栈中元素
int top;
}SqStack;
注意:
- 结构体数组访问结构体内成员时用:’ . ',如: S . t o p , S . d a t a [ i ] S.top,S.data[i] S.top,S.data[i]
- 结构体指针访问结构体内成员时用:’ -> ',如: L − > n e x t L->next L−>next
2.初始化
初始时,结构体数组内还未存放元素,因此,不存在栈顶元素,令 top=-1
代码实现:
void InitStack(SqStack &S) {
S.top = -1;//初始化栈顶指针
}
3.判空&判满
由于顺序栈的入栈操作受数组时上界限制,所以可能发生栈上溢,此时 t o p = M a x s i z e − 1 top=Maxsize-1 top=Maxsize−1;
同理,当栈空时, t o p = − 1 top=-1 top=−1
所以,栈满或栈空时,栈顶指针top指向data所在内存空间的两端
代码实现:
//1.判空
bool Empty(SqStack& S) {
if (S.top == -1) //栈空
return true;
else
return false;
}
//2.判满
bool StackOver(SqStack& S) {
if (S.top == Maxsize - 1)
return true;
else
return false;
}
4.入栈
入栈,由于只能在栈顶操作,所以当栈不满时,执行两个操作(不能反):
① 先让栈顶指针向后移一位:S.top++
② 再让在当前栈顶指针的位置加入元素 x:S.data[S.top]=x
最终合并为:S.data[++top]=x;
代码实现:
bool Push(SqStack& S, int x) {
if (S.top == Maxsize - 1) //栈满
return false;
//S.top = S.top + 1;
//S.data[S.top] = x;
S.data[++S.top] = x;
return true;
}
5.出栈
出栈也是只能在栈顶操作,执行两个操作(不能反):
① 先记录栈顶元素x:x=S.data[top]
② 再在逻辑上删除x,让栈顶指针前移一位:S.top--
最终合并为:S.data[top--]=x;
代码实现:
bool Pop(SqStack& S, int &x) {
if (S.top == -1)
return false;
//x = S.data[S.top];
//S.top = S.top - 1;
x = S.data[S.top--];
return true;
}
6.顺序栈的完整实现
完整代码实现:
#include输出结果:
3.共享栈
1.共享栈的定义
由于顺序栈需要在定义时开辟一整片连续的内存空间,对空间的利用率低,因此,我们考虑对其进行优化成为共享栈
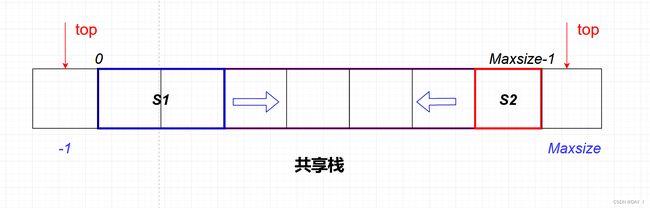
共享栈:利用了栈底的不变性,可以让两个栈共用所开辟的一维数组空间,将两个栈底分别设置在共享栈的两端,两个栈顶向共享空间的中间延伸
共享栈图示:
共享栈的优点:节省存储空间,降低发生上溢的可能性
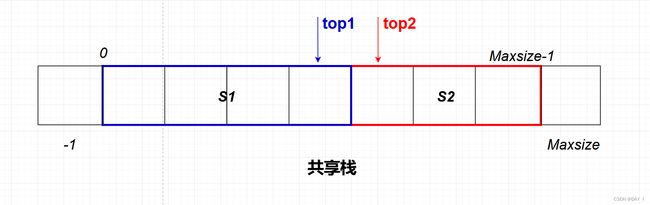
由于在一片内存空间中有两个栈,即两个栈顶指针 t o p 1 , t o p 2 top1,top2 top1,top2,所以,共享栈的结构体定义如下:
#define Maxsize 50
typedef struct Stack {
int data[Maxsize];
int top1;
int top2;
}Stack;
2.初始化
初始化需要对两个指针进行操作, t o p 1 , t o p 2 top1,top2 top1,top2分别指向一维数组空间的 两端
代码实现:
void InitStack(Stack& S) {
S.top1 = -1;
S.top2 = Maxsize;
}
3.判空&判满
①对于判空:
S 1 S1 S1的判空为:top1=-1; S 2 S2 S2的判空为:top2=Maxsize
①对于判满:
代码实现:
//1.栈空
bool Empty(Stack& S,int i) { //i表示访问的是栈Si
if (i == 1 && S.top1 == -1)
return true;
if (i == 2 && S.top2 == Maxsize)
return true;
return false;
}
//2.栈满
bool StackOver(Stack& S, int i) {
if (S.top2 - S.top1 == 1)
return true;
return false;
}
4.入栈
入栈时,S1为栈顶指针向后移动一位,S2为栈顶指针向前移动一位,但要先判断合法性
代码实现:
bool Push(Stack& S, int i,int x) {
if (i < 1 || i>2) {
cout << "访问的栈不存在" << endl;
return false;
}
if (StackOver(S)) {
cout << "栈满" << endl;
return false;
}
switch (i) { //对i进行条件分类
case 1:
S.data[++S.top1] = x;
return true;
break;
case 2:
S.data[--S.top2] = x;
return true;
}
}
5.出栈
同理,出栈时,S1的栈顶指针向前移动一位,S2的栈顶指针向后移动一位,也要先判断合法性
注意:这里判断合法性时,对于S1,S2的判断不再相同
代码实现:
//出栈
bool Pop(Stack& S, int i,int x) {
if (i < 1 || i>2) {
cout << "访问的栈不存在" << endl;
return false;
}
switch (i) {
case 1:
if (Empty(S, 1)) {
cout << "S1栈空" << endl;
return false;
}
else {
x = S.data[S.top1--];
return true;
}
break;
case 2:
if (Empty(S, 2)) {
cout << "S2栈空" << endl;
return false;
}
else {
x = S.data[S.top2++];
return true;
}
}
}
6.共享栈的完整实现
完整代码实现:
#include输出结果:
4.链栈
1.链栈的定义
链栈:采用链式存储的栈,是特殊的受限制的单链表,其规则是:所有的操作都必须在单链表表头进行
链栈的优点:
- 便于多个栈共享存储空间和提高效率
- 不存在栈满上溢的情况
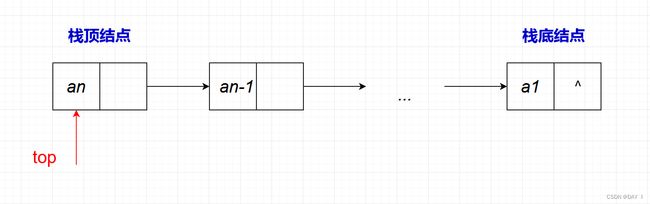
栈的链式存储结构:
进栈顺序: a 1 − > a 2 − > . . . − > a n a_1->a_2->...->a_n a1−>a2−>...−>an
定义链栈的结点(不带头结点):
typedef struct LinkNode {
int data;
struct LinkNode* next;
}LinkNode,*LiStack;
2.初始化
这里默认是不带头结点的链栈
void InitStack(LiStack& S) {
S = NULL;
}
3.判空
链栈没有判满,除非内存分配不足
bool Empty(LiStack& S) {
if (S == NULL)
return true;
return false;
}
4.入栈
即单链表的 前插操作:
①开辟一片内存空间存放新结点 p p p:p->data=x;
注意要判断是否开辟成功,防止内存分配不足
②让 t o p top top 指针指向 p p p:S=p;
这里头指针 S S S即充当了 t o p top top指针
代码实现:
bool Push(LiStack& S,int x) {
LinkNode* p = (LinkNode*)malloc(sizeof(LinkNode));
if (p == NULL) //内存分配不足
return false;
p->data = x;
p->next = S;
S = p;
return true;
}
5.出栈
即删除单链表的首结点:
①用 x x x记录首结点的数据:x=S->data;
②让 t o p top top 指针指向下一个结点,逻辑上删除首结点:S=S->next;
代码实现:
#include输出结果:
二. 队列
1.了解队列
什么是队列?
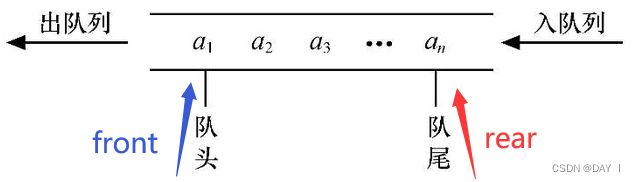
队列:只允许在表的一端进行插入,另一端进行删除( F I F O FIFO FIFO) (也是一种特殊的操作受限的线性表)
队列的图示:
2.队列的顺序存储结构
1.顺序队列的定义
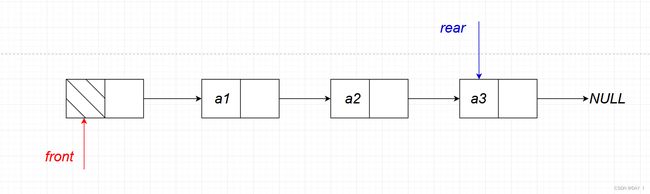
队列的顺序存储结构:分配一块连续的存储单元存放队列中的元素,并附设两个指针, f r o n t front front指向队头元素, r e a r rear rear指向队尾元素的下一个元素
删除元素在队头 f r o n t front front,插入元素在队尾 r e a r rear rear
顺序队列的结构体定义:
#define Maxsize 50
typedef struct SqQueue {
int data[Maxsize];
int front, rear;
}SqQueue;
基本操作:
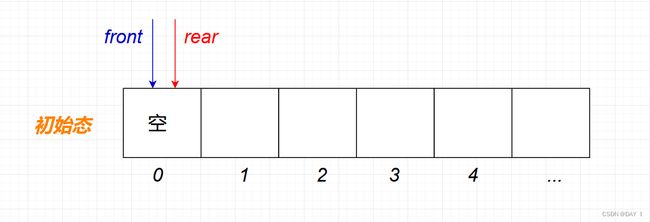
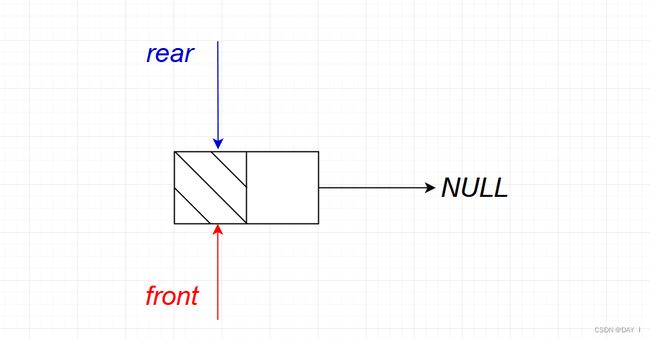
初始状态:Q.front==Q.rear
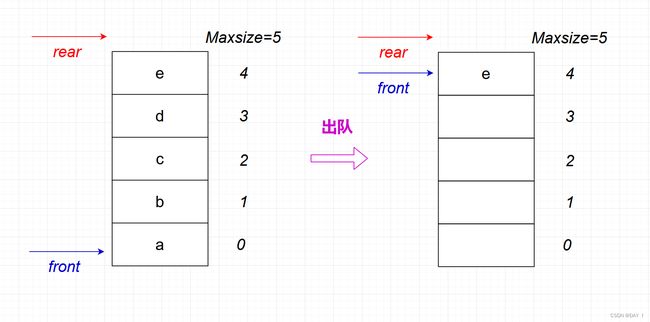
入队操作:队不满时,先送值到队尾元素,再将队尾指针 r e a r + 1 rear+1 rear+1
出队操作:队不空时,先取队头元素元素值,再将队头指针 f r o n t + 1 front+1 front+1
2.判空&判满 ?
顺序存储下,队列的判空和判满就很有意思了
我们对上述初始化的队列中增加一个元素(入队)
可以看到, r e a r rear rear与 f r o n t front front已经不指向一片空间,只有为空时,队头才会和下一个要插入的位置重合,所以,当队列为空时, Q . f r o n t = = Q . r e a r Q.front==Q.rear Q.front==Q.rear
那按照之前顺序存储所说的,队满时的条件就是: Q . r e a r = = M a x s i z e Q.rear==Maxsize Q.rear==Maxsize 吗?
此时,我们并没有在队列中插入元素,所以,队尾指针 r e a r rear rear不会改变,而删除元素导致 f r o n t front front不断后移, Q . r e a r = M a x s i z e Q.rear=Maxsize Q.rear=Maxsize而删除的元素空间已经空出来了,可以存放新元素,这是称为"假上溢",所以,无法单凭 r e a r rear rear的值就判定队满
所以,我们采取 取余 的操作,实现队满的判断
当我们插入一个元素时,我们先令 a [ Q . r e a r ] = x a[Q.rear]=x a[Q.rear]=x,此时,进行判断:若 ( Q . r e a r + 1 ) % M a x s i z e = f r o n t (Q.rear+1)\% Maxsize=front (Q.rear+1)%Maxsize=front,那么我们则可以判断——队满!
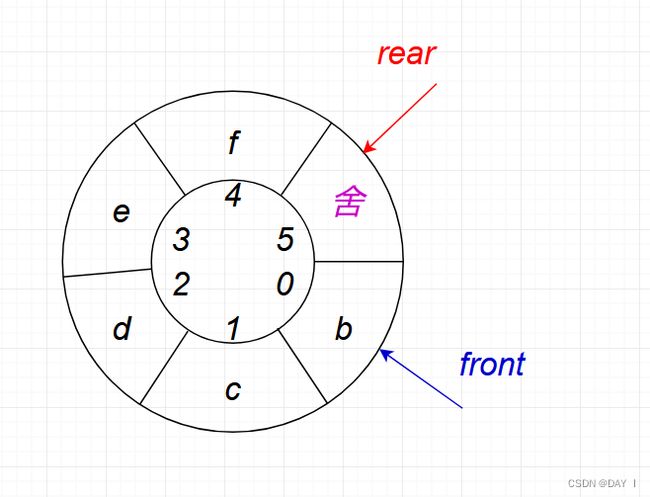
图解:
若此时 f r o n t front front指向 3 3 3, r e a r rear rear指向 2 2 2,需要插入一个新元素x:
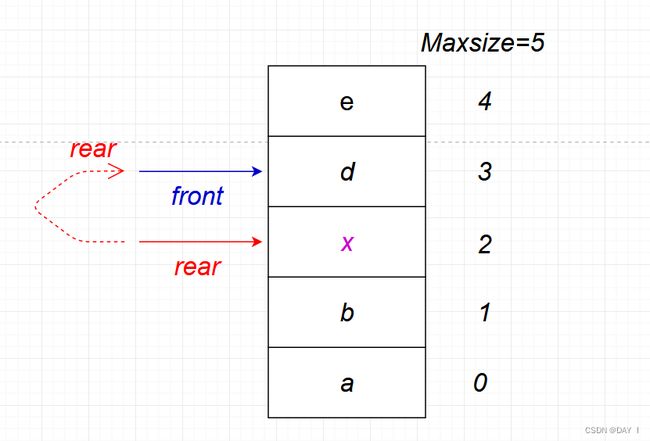
在移动 r e a r rear rear之前,我们先判断 r e a r rear rear和 f r o n t front front的关系: ( 2 + 1 ) % 5 = 3 (2+1)\%5=3 (2+1)%5=3,所以,队满
但是此时又存在一个新的问题就是, Q . f r o n t = = Q . r e a r Q.front==Q.rear Q.front==Q.rear,而这是队空的条件,但这是有是队满的状态,所以,队列的顺序存储的缺陷就是:难以分清队空&队满
3.循环队列
1.了解循环队列
在了解了顺序存储的缺陷之后,我们用循环队列进行优化
循环队列:将顺序队列改造为一个环形的空间,此时,当队首指针 Q . f r o n t = M a x s i z e − 1 Q.front=Maxsize-1 Q.front=Maxsize−1后,再进一个位置就会回到 0(通过 取余 实现)
这里只是逻辑上视为一个环,所以定义方式不变,只是初始化会改变:
void InitQueue(SqQueue& Q) {
Q.front = Q.rear = 0; //队头队尾指针指向0
}
基本操作:
- 初始化: Q . f r o n t = Q . r e a r = 0 Q.front=Q.rear=0 Q.front=Q.rear=0
- 队首指针进1: Q . f r o n t = ( Q . f r o n t + 1 ) % M a x s i z e Q.front=(Q.front+1)\%Maxsize Q.front=(Q.front+1)%Maxsize
- 队尾指针进1: Q . r e a r = ( Q . r e a r + 1 ) % M a x s i z e Q.rear=(Q.rear+1)\%Maxsize Q.rear=(Q.rear+1)%Maxsize
- 队列长度: l e n = ( Q . r e a r + M a x s i z e − Q . f r o n t ) % M a x s i z e len=(Q.rear+Maxsize-Q.front)\%Maxsize len=(Q.rear+Maxsize−Q.front)%Maxsize
那么,队满和队空的条件又是什么呢?显然,队空的条件是 Q . f r o n t = = Q . r e a r Q.front==Q.rear Q.front==Q.rear,若入队元素的速度快于出队元素的速度,则尾指针很快会追上首指针,如图,当循环队列队满的时候,同样也有 Q . f r o n t = = Q . r e a r Q.front==Q.rear Q.front==Q.rear
因此,对于队空还是队满的判断,有三种方法:
2. 牺牲单元法
牺牲一个单元来区分队空和队满,入队时少用一个队列单元
以队头指针在队尾指针的下一位置作为队满的标志
- 队满条件: ( Q . r e a r + 1 ) % M a x s i z e = = Q . f r o n t (Q.rear+1)\%Maxsize==Q.front (Q.rear+1)%Maxsize==Q.front
- 队空条件: Q . r e a r = = Q . f r o n t Q.rear==Q.front Q.rear==Q.front
图解:
1. 队空:
bool Empty(SqQueue& Q) {
if (Q.rear == Q.front)
return true;
return false;
}
2. 队满:
bool Over(SqQueue& Q) {
if ((Q.rear + 1) % Maxsize == Q.front)
return true;
return false;
}
3. 出队:
bool DeQueue(SqQueue& Q, int& x) {
if (Empty(Q))
return false;
x = Q.data[Q.front];
Q.front = (Q.front + 1) % Maxsize; // 头移
return true;
}
4. 入队:
bool EnQueue(SqQueue& Q, int x) {
if (Over(Q))
return false;
Q.data[Q.rear] = x;
Q.rear = (Q.rear + 1) % Maxsize; // 尾移
return true;
}
3. tag法
在结构体中新设一个 t a g tag tag数据成员,以区分是队满还是队空
判断依据:
当 Q . t a g = = 0 Q.tag==0 Q.tag==0时,若因删除导致 Q . r e a r = = Q . f r o n t Q.rear == Q.front Q.rear==Q.front,则为队空
当 Q . t a g = = 1 Q.tag==1 Q.tag==1时,若因插入导致 Q . r e a r = = Q . f r o n t Q.rear == Q.front Q.rear==Q.front,则为队满
进队时置 tag为1,出队时置tag为0,因为只有入队才会导致队满,出队才会导致队空
- 队空条件: Q . r e a r = = Q . f r o n t Q.rear == Q.front Q.rear==Q.front 且 Q . t a g = = 0 Q.tag==0 Q.tag==0
- 队满条件: Q . r e a r = = Q . f r o n t Q.rear == Q.front Q.rear==Q.front 且 Q . t a g = = 1 Q.tag==1 Q.tag==1
- 进队操作: Q . d a t a [ Q . r e a r ] = x Q.data[Q.rear]=x Q.data[Q.rear]=x ; Q . r e a r = ( Q . r e a r + 1 ) % M a x s i z e Q.rear=(Q.rear+1)\%Maxsize Q.rear=(Q.rear+1)%Maxsize; Q . t a g = 1 Q.tag=1 Q.tag=1
- 出队操作: x = Q . d a t a [ Q . f r o n t ] x=Q.data[Q.front] x=Q.data[Q.front] ; Q . f r o n t = ( Q . f r o n t + 1 ) % M a x s i z e Q.front=(Q.front+1)\%Maxsize Q.front=(Q.front+1)%Maxsize ; Q . t a g = 0 Q.tag=0 Q.tag=0
1. 入队:
int EnQueue(SqQueue &Q,int x){
if(Q.front==Q.rear && Q.tag=1) //队满条件
return 0;
Q.data[Q.rear]=x;
Q.rear=(Q.rear+1)%Maxsize;
Q.tag=1; // 标记
return 1;
}
2. 出队:
int DeQueue(SqQueue &Q,int &x){
if(Q.rear==Q.front && Q.tag==0) //队空条件
return 0;
x=Q.data[Q.front];
Q.front=(Q.front+1)%Maxsize;
Q.tag=0; // 标记
return 1;
}
4. size法
类型中增设表示元素个数的size成员
入队则 Q . s i z e + 1 Q.size+1 Q.size+1 ;出队则 Q . s i z e − 1 Q.size-1 Q.size−1
这样,队空的条件为 Q . s i z e = = 0 Q.size==0 Q.size==0 ;队满的条件为 Q . s i z e = = M a x s i z e Q.size==Maxsize Q.size==Maxsize 这两种情况都有 Q . f r o n t = = Q . r e a r Q.front==Q.rear Q.front==Q.rear
4.队列的链式存储结构
1.链队列的定义
对于顺序存储下的队列,在实现一些基本操作时很不方便,因此,我们用链式存储进行优化
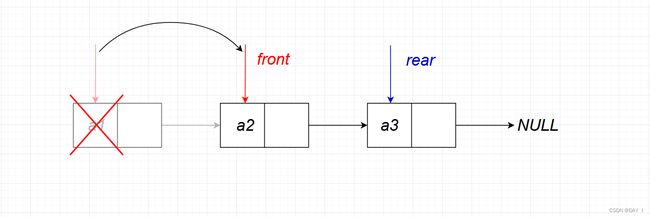
链队列:即队列的链式存储,它实际上是一个同时带有队头指针 f r o n t front front 和队尾指针 r e a r rear rear 的单链表, f r o n t front front 指向队头, r e a r rear rear 指向队尾
队列的链式存储结构:
带头结点
值得注意的是,这个单链表只能在首结点进行删除操作、在尾结点进行插入操作
链队列的优点:
- 链队列适合数据变动较大时
- 不存在队列满且产生溢出的情况
链队列的结构体定义:
typedef struct LinkNode {
Elemtype data;
struct LinkNode* next;
}LinkNode;
typedef struct LinkQueue{
struct LinkNode* front, * rear;
}LinkQueue;
这里需要定义两个结构体:一个是单链表结点的结构体 L i n k N o d e LinkNode LinkNode,包含 d a t a data data数据域和 n e x t next next指针域,另一个是代表链队列整体的结构体 L i n k Q u e u e LinkQueue LinkQueue,包含 头指针 f r o n t front front和尾指针 r e a r rear rear
2.初始化
对于链队列的基本操作,我们分成带头结点和不带头结点进行讨论
1.不带头结点
不带头结点时,头指针直接指向链表的第一个结点,初始化头指针和尾指针均指向 N U L L NULL NULL
代码实现:
void InitQueue(LinkQueue& Q) {
Q.front = NULL;
Q.rear = NULL;
}
2.带头结点
而带头结点时,头指针将始终指向头结点,不会因为删除操作移动,同样也要让头指针和尾指针指向同一位置
代码实现:
void InitQueue(LinkQueue& Q) {
Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));
Q.front->next = NULL;
}
3.判空
由于链式存储并不存在队满的情况,因此只需讨论队空的条件
1.不带头结点
对于不带头结点的链队列,头指针始终指向首结点,而当队空时, f r o n t front front只能指向 N U L L NULL NULL
代码实现:
//判队空
bool EmptyQueue(LinkQueue Q) {
if (Q.front == NULL) //因为只要有结点存在,front一定指向第一个结点
return true;
return false;
}
2.带头结点
带头结点时, f r o n t front front始终指向头结点而不会指向 N U L L NULL NULL,所以我们根据它的初始化条件判断是否为空:
即当 Q . f r o n t = = Q . r e a r Q.front == Q.rear Q.front==Q.rear (也就是头指向头结点时) 链队列为空
代码实现:
//判队空
bool EmptyQueue(LinkQueue Q) {
if (Q.front == Q.rear) //因为只要有结点存在,rear一定会移动
return true;
return true;
}
4.入队
1.不带头结点
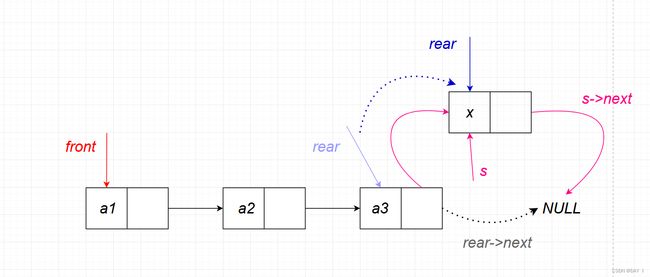
当加入一个新结点 x x x 时,由于是在队尾进行操作,因此,让指向新结点的指针 s s s 的下一个指向 r e a r rear rear 的下一个位置:s->next=Q.rear->next ,连接尾结点和新结点:Q.rear->next=s,再移动尾指针到现在的 s s s 位置: Q.rear=s
而不带头结点的入队要比带头结的繁琐,原因是对于链表为空时要进行特判
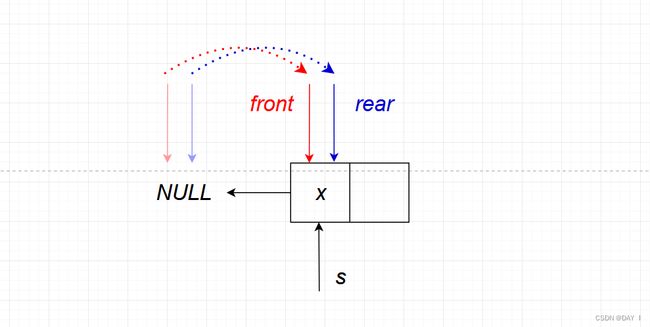
当链队列为空时,由于 f r o n t front front 和 r e a r rear rear 均指向 N U L L NULL NULL,因此:
① 不能直接让:s->next=Q.rear->next ❌;而是 s->next=NULL √
② 在加入新结点后,不仅要让: Q.rear=s,还要令头指针指向第一个结点: Q.front=s
代码实现:
//入队
void EnQueue(LinkQueue& Q, Elemtype x) {
LinkNode* s = (LinkNode*)malloc(sizeof(LinkNode));
s->data = x;
s->next = NULL; //这时候不能用尾指针的下一个指针了,因为尾指针有可能指向NULL
if (Q.front == NULL) { //Q.rear==NULL
Q.front = s; //头结点也要跟着变
Q.rear = s;
}
else {
Q.rear->next = s; //Q.rear!=NULL
Q.rear = s;
}
}
2.带头结点
而对于带头结点的入队操作就要方便很多,因为头结点的存在,所以即使链队列为空, f r o n t front front 和 r e a r rear rear 是指向头结点而不是 N U L L NULL NULL,这实现了操作上的统一
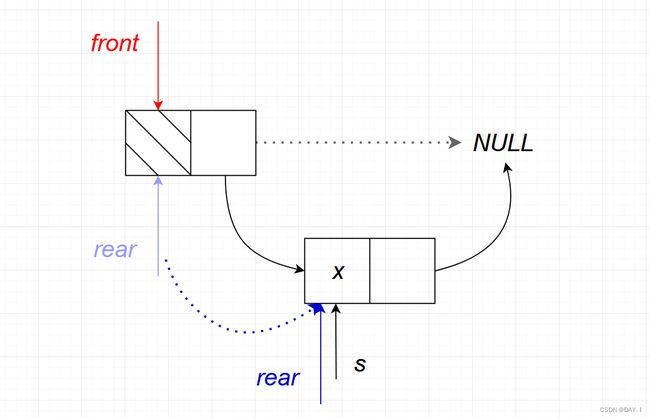
代码实现:
//入队
void EnQueue(LinkQueue& Q, Elemtype x) {
LinkNode *s = (LinkNode*)malloc(sizeof(LinkNode));
s->data = x;
s->next = Q.rear->next;
Q.rear->next = s;
Q.rear = s;
}
5.出队
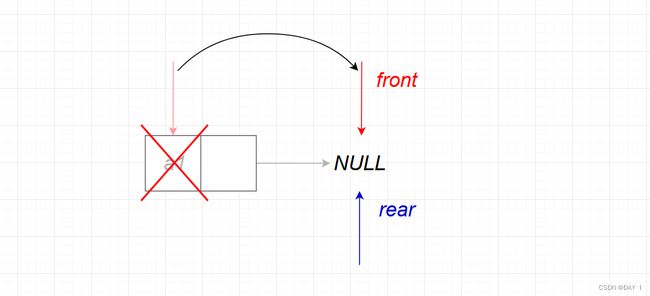
1.不带头结点
出队操作在队头进行,因此,需要不断移动队头指针 f r o n t front front 进行逻辑上的删除操作:p=Q.front ,Q.front=p->next,最后释放结点 free§
但是,还存在特殊情况
①链队列为空:
也就是当 Q.front=NULL 时,则出队失败 return false
②链队列中只有一个结点(即要删除的结点为尾结点):
这时候,特殊的是,不仅要移动头指针: Q.front=NULL;还需要移动尾指针: Q.rear=NULL
代码实现:
//出队
bool DeQueue(LinkQueue& Q, Elemtype& x) {
if (Q.front == NULL)
return false;
LinkNode* p = (LinkNode*)malloc(sizeof(LinkNode));
p = Q.front; //即为第一个结点
x = p->data;
Q.front = p->next;
if (Q.rear == p){ //如果要删除的p就是尾结点
Q.rear = NULL;
Q.front = NULL; //没有头结点,都指向NULL
}
free(p);
return true;
}
2.带头结点
带头结点时出队的操作与不带头结点时相似,也必须进行:①判空;②判断出队结点是否为尾结点,只是此时的操作对象变为: p=Q.front->next
代码实现:
//出队
bool DeQueue(LinkQueue& Q, Elemtype& x) {
if (Q.rear == Q.front)
return false;
LinkNode* p = (LinkNode*)malloc(sizeof(LinkNode));
p = Q.front->next;
x = p->data;
Q.front->next = p->next;
if (Q.rear == p) //如果要删除的p就是尾结点
Q.rear = Q.front;
free(p);
return true;
}
5.双端队列
1.了解双端队列
双端队列的形式变换多样,操作灵活,需要熟练掌握
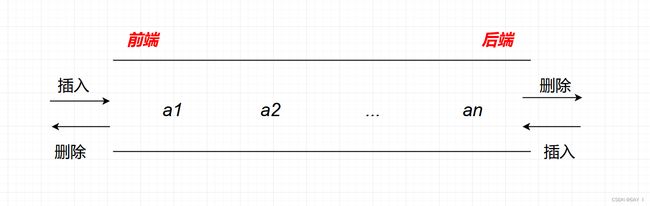
双端队列:两端都可以进行入队和出队操作的队列,其逻辑结构仍为线性结构,队列的两端则称为前端和后端
双端队列的结构:
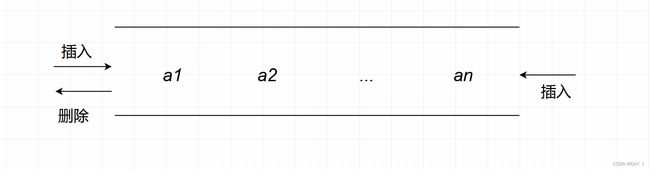
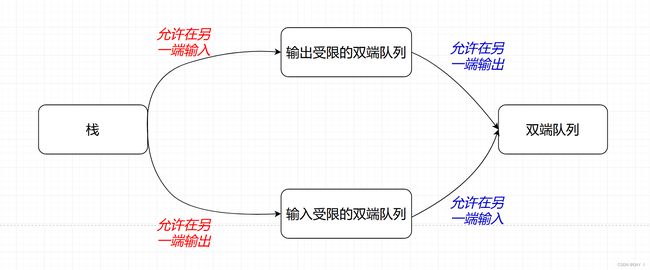
2.受限的双端队列
①输出受限的双端队列:允许在一端进行插入和删除操作,但在另一端只允许插入的队列
②输入受限的双端队列:允许在一端进行插入和删除操作,但在另一端只允许删除的队列
若限定一般的双端队列从某个端点插入的元素只能从该端点删除,则这个双端队列可以视为两个栈底相邻接的栈
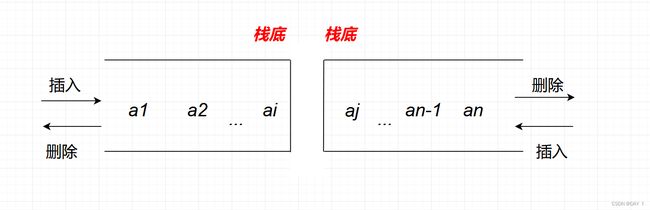
3.双端队列的操作
e . g e.g e.g 设有一个双端队列,输入序列为 1 , 2 , 3 , 4 1,2,3,4 1,2,3,4,要求得到如下的输出序列:
- 能由输入受限的双端队列得到,而不能由输出受限的双端队列得到的输出序列
- 能由输出受限的双端队列得到,而不能由输入受限的双端队列得到的输出序列
- 既不能由输入受限的双端队列得到,又不能由输出受限的双端队列得到的输出序列
首先,由四种结构的关系可以得出:
①栈能实现的输出序列,其他三种结构一定能实现
②出限的双端队列和入限的双端队列能实现的输出序列,双端队列一定能实现
而双端队列能实现的输出序列为: A 4 4 = 24 A_4^4=24 A44=24 种,栈能实现的输出序列为(卡特兰数): 1 n + 1 C 8 4 = 14 \frac {1} {n + 1}C_{8}^{4}=14 n+11C84=14 种
因此,只需要检查剩下10种情况,依次判断出限和入限的双端队列能否实现即可
这里直接给出结果:
1. 出限不能实现的输出序列为: 4 , 2 , 3 , 1 4,2,3,1 4,2,3,1 和 4 , 1 , 3 , 2 4,1,3,2 4,1,3,2
判断出限输出序列的方法:
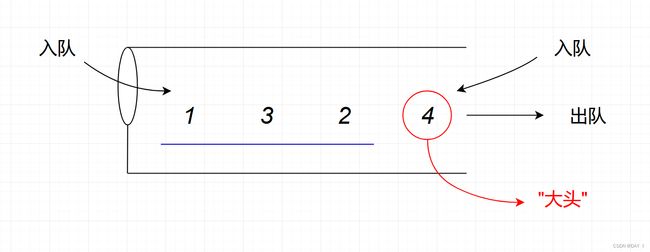
画"带孔的栈"法—看输出序列:
画一个栈,实现一端输入和输出,并且在栈底开一个小孔表示只能输入,由于只能由一端输出,我们抓住所要验证的输出序列的"大头",则比这个数小的数在"大头"出队之前一定已经全部进入"栈"内按出队顺序排列好了,所以我们只需要验证能否通过两端的交替输入操作实现这些数的当前排序方式
按照此方法,我们来验证上述两种输出序列:
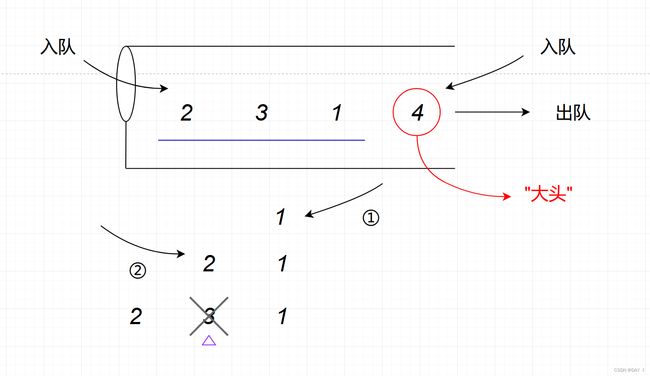
抓"大头",此时最先出队的数为 4 4 4,比 4 4 4小的有 1 , 2 , 3 1,2,3 1,2,3,由于栈的出栈顺序就是这些数在栈中的排列顺序,所以可以得到如下排列的栈,其中 1 , 2 , 3 1,2,3 1,2,3 的排列为: 1 , 3 , 2 1,3,2 1,3,2
我们尝试通过两端交替输入得到排列 1 , 3 , 2 1,3,2 1,3,2 :
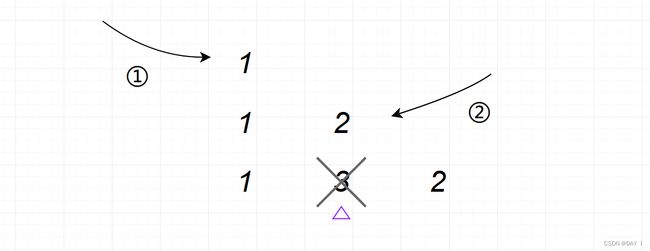
可以看到,此时 3 3 3 夹在 1 1 1 和 2 2 2 中间,不论两端怎么输入,都不可能将 3 3 3 放入,因此,这种序列无法由出限队列得到
同理,可以判断,对于 4 , 2 , 1 , 3 4,2,1,3 4,2,1,3 也无法由出限队列得到:
2. 入限不能实现的输出序列为: 4 , 2 , 3 , 1 4,2,3,1 4,2,3,1 和 4 , 2 , 1 , 3 4,2,1,3 4,2,1,3
判断入限输出序列的方法:
画队列法—看输入序列:
画一个队列,由于该队列能从两端删除,而只能从一端输入,因此,我们首先抓输出序列的"大头",比它小的数在大头出队之前一定已经进入队列了,且由于只能一端输入,所以我们只需要看输入序列中这些数的排列顺序,就可以确定这些数在队列中的排列,这时我们只需验证能否通过两端的交替输出操作实现该输出排列即可
按照此方法,我们也来验证上述两种输出序列:
首先抓"大头",最先输出的数为 4 4 4,所以在 4 4 4 之前的数 1 , 2 , 3 1,2,3 1,2,3 此时一定已经入队,而根据输入序列为 1 , 2 , 3 , 4 1,2,3,4 1,2,3,4,则可以确定,队列中的排列为: 4 , 3 , 2 , 1 4,3,2,1 4,3,2,1
我们尝试通过两端的交替输出得到上述两种输出序列:
可以看到,无论如何都无法得到 2 2 2 比 1 1 1 o r or or 3 3 3 先出队的输出序列
所以可以得出,既不能由输入受限的双端队列得到,又不能由输出受限的双端队列得到的输出序列为: 4 , 2 , 3 , 1 4,2,3,1 4,2,3,1