遗传算法(GA)解决MTSP问题及Matlab代码
本篇文章是利用遗传算法来解决MTSP或者MVRP问题的,至于遗传算法较为详尽的介绍的话,在我上一篇文章中有介绍,这里就不再啰嗦了。
1、问题简述
在本文中,MTSP问题就是有一组旅行者需要遍历完给定的所有城市,并且回到起点,要求其总体的旅行距离为最小;MVRP问题就是把一组旅行者变为一组机器人而已。在本文中所有旅行者的起点是不确定的,也就是说旅行者可以随机从一个城市出发,并且在最后要回到起点城市。假设旅行者人数为nSalesmen = k,城市位置为xy,那么整体的图会有K个回路,且K个回路中没有子回路了。
城市位置分布图
2、染色体编码问题
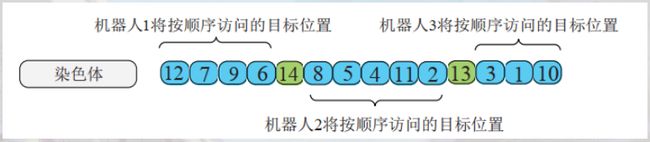
染色体编码方式采用的仍然是十进制编码方式,与TSP问题不同的是:每一个个体都会有一个与之相对应的染色体分隔点的集合。把染色体进行分隔的目的是区别每一个旅行者的路径。如下图所示,假设有3个机器人,需要去访问14个城市,则染色体就是14个城市序号的随机排列,3个机器人则对应有两个分隔点标记,如图产生的两个分隔点标记为5和11的位置。
染色体分隔演示
若每一个旅行者有最小旅行城市的限制的话,也就是每一个旅行者至少需要旅行minTour个城市的话,染色体分隔点会有所不同。集中在染色体前端的位置作为分隔点的概率会小很多,且分隔点与分隔点之前必须要有minTour个城市,则需要根据概率来限制分隔点的选择了。
3、遗传算法流程
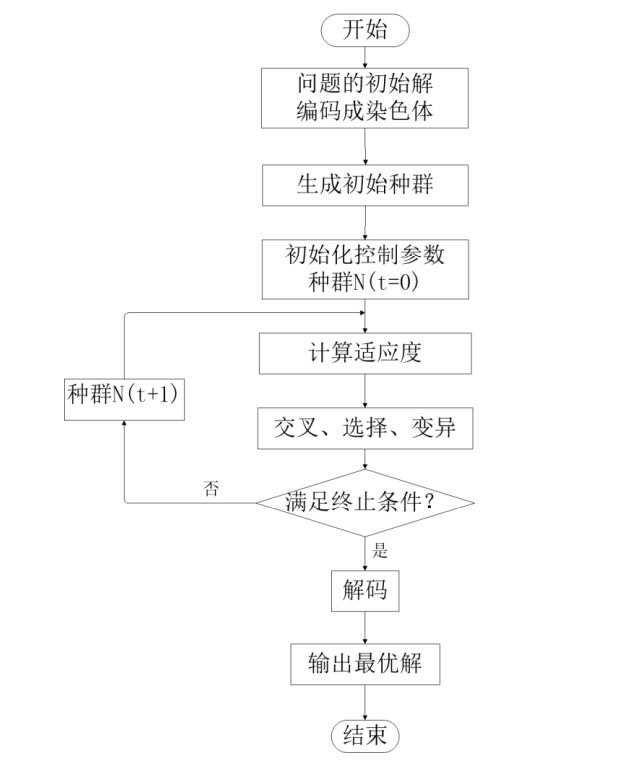
重新回顾一下遗传算法的流程吧!
GA流程
在本文中问题的初始解包括旅行者初始路线的初始化和染色体分隔点的初始化,两者是一一对应的关系。
4、Matlab代码及其结果
function varargout = mtsp_ga(xy,dmat,nSalesmen,minTour,popSize,numIter,showProg,showResult)
%若无参数输入,参数初始化
nargs = 8;
for k = nargin:nargs-1
switch k
case 0
xy = 100*rand(50,2);%随机生成50个城市坐标,rand(0~1)
case 1
N = size(xy,1);%城市个数
a = meshgrid(1:N);%生成N*N升序矩阵
dmat = reshape(sqrt(sum((xy(a,:)-xy(a',:)).^2,2)),N,N);%计算距离矩阵。装置,生成N*N的距离矩阵
case 2
nSalesmen = 5;%旅行者个数
case 3
minTour = 3;%最小旅行距离
case 4
popSize = 80;%种群个数
case 5
numIter =5e3;%迭代次数
case 6
showProg =1;%展示迭代过程
case 7
showResult = 1;%展示最终结果
otherwise
end
end
%对输入参数进行扫描
[N,dims] = size(xy);%城市个数、维数
[nr,nc] = size(dmat);%距离矩阵的行数和列数
if N~=nr||N~=nc
error('城市坐标或距离矩阵输入错误')
end
n =N;
%数据检查
nSalesmen = max(1,min(n,round(real(nSalesmen(1)))));
minTour = max(1,min(floor(n/nSalesmen),round(real(minTour(1)))));
popSize = max(8,8*ceil(popSize(1)/8));
numIter = max(1,round(real(numIter(1))));
showProg = logical(showProg(1));%将数值转变为逻辑值
showResult=logical(showResult(1));
%初始化路径分隔点(染色体分隔点)
nBreaks = nSalesmen -1;
dof = n - minTour*nSalesmen; %自由城市数目
addto = ones(1,dof+1);%余下插入的位置剩下25个,可供插入
for k = 2:nBreaks
addto = cumsum(addto);%累加
end
cumProb = cumsum(addto)/sum(addto);
%% 初始化种群
popRoute = zeros(popSize,n);%80个体
popBreak = zeros(popSize,nBreaks);%每个种群都有特定的分隔点
popRoute(1,:) = (1:n);%第一个种群为1到50的升序排列
popBreak(1,:) = rand_breaks();%随机生成第一个分隔种群
for k = 2:popSize
popRoute(k,:) = randperm(n);
popBreak(k,:) = rand_breaks();
end
%选择画图颜色
pclr = ~get(0,'DefaultAxesColor');
clr = [1 0 0;0 0 1;0.67 0 1;0 1 0;1 0.5 0];
if nSalesmen > 5
clr = hsv(nSalesmen);%根据机器人的数量来确定画图需要多少种颜色
end
%运行遗传算法
globalMin = Inf;
totalDist = zeros(1,popSize);%每个个体的路径长度
distHistory = zeros(1,numIter);%每一代的最优距离
tmpPopRoute = zeros(8,n);
tmpPopBreak = zeros(8,nBreaks);
newPopRoute = zeros(popSize,n);
newPopBreak = zeros(popSize,nBreaks);
if showProg
pfig = figure('Name','MTSP_GA | Current Best Solution','Numbertitle','off');
end
for iter = 1:numIter
%% 计算每一个个体的总旅行距离
for p = 1:popSize
d = 0;
pRoute = popRoute(p,:);
pBreak = popBreak(p,:);
rng = [[1 pBreak+1];[pBreak n]]';%代表了每一个旅行商的起点和终点
for s =1:nSalesmen %计算这一种群的总距离
d = d + dmat(pRoute(rng(s,2)),pRoute(rng(s,1)));
for k = rng(s,1):rng(s,2)-1 %计算旅行商中间的距离
d = d + dmat(pRoute(k),pRoute(k+1));
end
end
totalDist(p) = d;%每一个个体的路径总长度
end
%% 找最优路径,若是当前最优则画出
[minDist,index] = min(totalDist);%距离、个体序号
distHistory(iter) = minDist;%记录这一代最佳路径距离
if minDist < globalMin
globalMin = minDist;
optRoute = popRoute(index,:);
optBreak = popBreak(index,:);
rng = [[1 optBreak+1];[optBreak n]]';%记录最佳路径分隔点
if showProg
figure(pfig);
for s =1:nSalesmen %画出最优路线
rte = optRoute([rng(s,1):rng(s,2) rng(s,1)]);%需要回到起点
if dims > 2,plot3(xy(rte,1),xy(rte,2),xy(rte,3),'.-','Color',clr(s,:),'LineWidth',2);
else plot(xy(rte,1),xy(rte,2),'.-','Color',clr(s,:),'LineWidth',2);
end
title(sprintf('总旅行距离 = %1.4f, 迭代次数 = %d',minDist,iter));
hold on
end
hold off
end
end
%% 采用锦标赛的方法进行选择,随机选择8个个体选择出最优个体作为父代
randomOrdor = randperm(popSize);%
for p = 8:8:popSize
rtes = popRoute(randomOrdor(p-7:p),:);
brks = popBreak(randomOrdor(p-7:p),:);
dists = totalDist(randomOrdor(p-7:p));
[~,idx] = min(dists);%找出距离最小的个体序号
bestof8Route = rtes(idx,:);
bestof8Break = brks(idx,:);
routeInsertionPoints = sort(ceil(n*rand(1,2)));%随机生成2个升序排列的插入点位置序号
I = routeInsertionPoints(1);
J = routeInsertionPoints(2);
for k =1:8
tmpPopRoute(k,:) = bestof8Route;
tmpPopBreak(k,:) = bestof8Break;
switch k
case 2 %让在插入点之间的城市进行翻转
tmpPopRoute(k,I:J) = tmpPopRoute(k,J:-1:I);
case 3 %变异,让两个随机点选中的城市进行交换
tmpPopRoute(k,[I J]) = tmpPopRoute(k,[J I]);
case 4% 随机点选中的城市片段进行迁移
tmpPopRoute(k,I:J) =tmpPopRoute(k,[I+1:J I]);
case 5
tmpPopBreak(k,:) = rand_breaks();%随机生成分隔点
case 6
tmpPopRoute(k,I:J)= tmpPopRoute(k,J:-1:I);
tmpPopBreak(k,:) = rand_breaks();
case 7
tmpPopRoute(k,[I J]) =tmpPopRoute(k,[I J]);
tmpPopBreak(k,:) = rand_breaks();
case 8
tmpPopRoute(k,I:J) =tmpPopRoute(k,[I+1:J I]);
tmpPopBreak(k,:) = rand_breaks();
otherwise
end
end
newPopRoute(p-7:p,:) = tmpPopRoute;
newPopBreak(p-7:p,:) = tmpPopBreak;
end
popRoute = newPopRoute;
popBreak = newPopBreak;
end
if showResult
figure('Name','MTSP_GA | Result','Numbertitle','off');
subplot(2,2,1);
if dims>2,plot3(xy(:,1),xy(:,2),xy(:,3),'.','Color',pclr);
else plot(xy(:,1),xy(:,2),'.','Color',pclr);end
title('城市位置');
subplot(2,2,2);
imagesc(dmat(optRoute,optRoute));
title('距离矩阵');
subplot(2,2,3);
rng = [[1 optBreak+1];[optBreak n]]';
for s = 1:nSalesmen
rte = optRoute([rng(s,1):rng(s,2) rng(s,1)]);
if dims>2, plot3(xy(rte,1),xy(rte,2),xy(rte,3),'.-','Color',clr(s,:));
else plot(xy(rte,1),xy(rte,2),'.-','Color',clr(s,:));
end
title(sprintf('旅行总距离 = %1.4f',minDist));
hold on;
end
subplot(2,2,4);
plot(distHistory,'b','LineWidth',2);
title('Best Solution History');
set(gca,'XLim',[0 numIter+1],'YLim',[0 1.1*max([1 distHistory])]);
end
if nargout
varargout{1} = optRoute;
varargout{2} = optBreak;
varargout{3} = minDist;
end
%% 若旅行者有旅行距离的要求的话,则在染色体前面位置选择分隔点的概率会偏低一点
%没有要求的话则可以随机生成分隔点
function breaks = rand_breaks()
if minTour ==1
tmpBreaks = randperm(n-1);%随机生成1~49的数组
breaks = sort(tmpBreaks(1:nBreaks));%在tmpbreaks1~7的位置产生分隔标记
else
nAdjust = find(rand < cumProb,1) -1;%返回cumProb中小于rand的索引cumProb在迭代中不会更新了
spaces = ceil(nBreaks*rand(1,nAdjust));%范围1~7
adjust = zeros(1,nBreaks);
for kk = 1:nBreaks
adjust(kk) = sum(spaces == kk);%spaces中与kk相等的相加
end
breaks = minTour*(1:nBreaks) + cumsum(adjust);
end
end
end
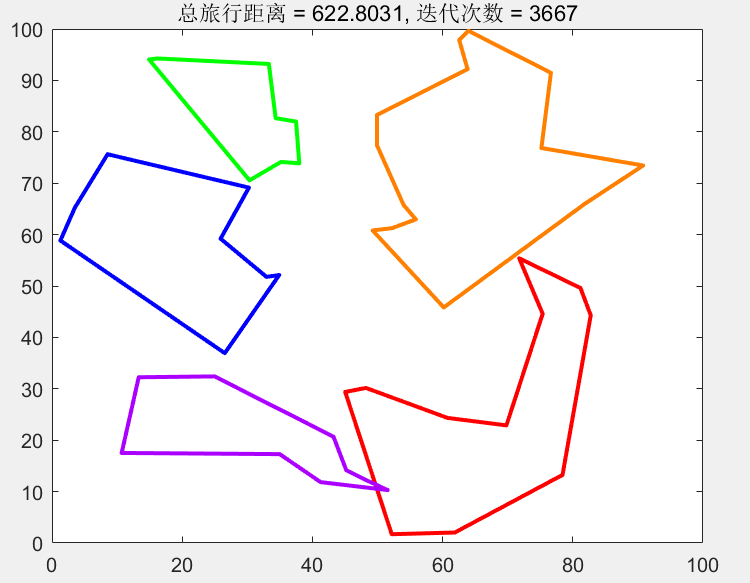
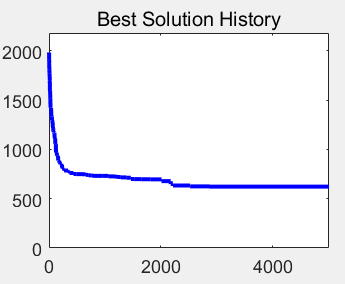
直接上结果!
若有小伙伴对机器人任务分配算法较为兴趣的,可以在下面评论交流一波,纯属互相学习!