连接(Join)算法
为什么需要JOIN?
- 范式化关系数据库中的表,以避免不必要的信息重复。
- 使用join可以在不丢失信息的情况下重建原始的tuple。
JOIN算法
我们将专注于使用 等值连接(inner equijoin) 等连接算法一次合并两个表。
- 这些算法可以调整以支持其他算法
通常,我们希望较小的表始终是查询计划中的左表(“out table”)。
JOIN操作的输出:数据
将外tuple和内tuple中的属性值复制到新的输出tuple中。
JOIN操作的输出:记录ID
只复制join keys和匹配tuple的记录ID。
- 非常适合列式存储,因为DBMS不复制查询不需要的数据。(考虑当一个表的属性有几千个而实际查询只需要几个属性时)
它被称为延迟物化(late materialization)
I/O开销分析
只关注I/O的使用次数而不关心实际得到输出结果的开销。
JOIN vs CROSS-PRODUCT
- R ⋈ S是最常见的操作,因此必须仔细优化。
- 其次是R × S,因为叉积的结果很大。
有很多方法可以减少join的开销,但没有一种可以在任何场景中都有效。
JOIN算法
嵌套循环连接(Nested Loop Join)
- 简单/愚蠢
- 块
- 索引
归并排序连接(Sort-Merge Join)
哈希连接(Hash Join)
嵌套循环连接
# 算法描述的伪代码
foreach tuple r ∈ R:
foreach tuple s ∈ S:
emit, if r and s match
该算法的愚蠢之处在于对于外表R中的每一个tuple,都要去扫描一遍内表S。
Cost: M + m * N
其中M为outer table R中的page数,m是R的tuple数,N是S的page数。
[例]一个数据库:
- 表R:M = 1000,m = 100,000
- 表S:N = 500,n = 40,000
开销分析
- M + (m * N) = 1000 + (100000 * 500) = 50,001,000 IOs
- 0.1ms/IO,总时间 ≈ 1.3 hours
如果用更小的表S作为外表呢?
- N + (n * M) = 500 + (40000 * 1000) = 40,000,500 IOs
- 0.1ms/IO,总时间 ≈ 1.1 hours
尽管快了一点,但还是很糟糕。
块嵌套循环连接
foreach block B_R ∈ R:
foreach block B_S ∈ S:
foreach tuple r ∈ B_R:
foreach tuple s ∈ B_S:
emit, if r and s match
将R表和S表分别读取到内存的两个block中,对于外表R的block中的每一个tuple,它们全部完成对S表的block中的每一个tuple的匹配、连接后,才重新读取S表的下一个block,当扫描过一遍S表后,重新读取R表的下一块block,重复前面的步骤。
该算法需要更少的磁盘访问:
- 对于R的每一个block,它扫描一遍S
- 开销:M + (M * N)
[例]一个数据库:
- 表R:M = 1000, m = 100,000
- 表S:N = 500, n = 40,000
开销:
- M + (M * N) = 1000 + (1000 * 500) = 501,000 IOs
- 0.1ms/IO,总时间 ≈ 50 seconds
这比之前的算法好很多了,但还是很糟糕。我们可以再进行一些改进,让时间减少到1秒内。
如果我们有B个缓冲块可以用呢?
- 使用B-2个缓冲块来扫描外表
- 使用一个缓冲块来存放内表,另一个缓冲块存储输出结果
foreach B-2 blocks b_R ∈ R:
foreach b_S ∈ S:
foreach tuple r ∈ b_R:
foreach tuple s ∈ b_S:
emit, if r and s match
该算法使用B-2个缓冲块来扫描R。
开销:M + (⌈M / (B-2)⌉ * N)
如果外表可以全部放进内存呢(B > M + 2)?
- 开销:M + N = 1000 + 500 = 1500 IOs
- 0.1ms/IO,总时间 ≈ 0.15 seconds
为什么基本的嵌套循环连接很糟糕?
对于外表的每一个tuple,我们必须顺序扫描去检验它和内表的每一个匹配。
我们可以使用索引来查找匹配以避免顺序扫描
- 为连接使用一个已存在的索引
- 建立临时索引(哈希表,B+树)
使用索引的循环嵌套连接
foreach tuple r ∈ R:
foreach tuple s ∈ Index(r_i = s_j):
emit, if r and s match
假设对于每一个tuple,每次索引探测的开销是一个常数C。比如,对于哈希表构建的索引,如果使用的是静态哈希表,有可能发生哈希到的slot被其它key占用的情况而必须向后扫描(线性探测),因为哈希表保存的是tuple所在的位置,所以会将page读进来遍历,如果没找到目标tuple,就要将哈希表下一个slot所记载的page读进来。在这里,平均开销为常数C。
开销:M + (m * C)
对于外表里的每一个tuple,经过索引探测后可以知道待连接的目标tuple所在的page,只要将那个page读进内存即可。我们不考虑连续的几个外表tuple是否有待连接的内表tuple在同一个page中的情况,仅仅是重复地对每个外表tuple,将内表tuple所在的page读入内存,即使这个page可能已经在内存当中了。
小结
- 选择较小的表作为外表
- 尽可能多的将外表缓存在内存中
- 循环遍历内表或使用索引
排序合并连接
阶段一:排序
- 对两个表按照连接键排序
- 我们可以使用外部排序算法
阶段二:合并 - 使用游标遍历两张已排序的表并匹配tuple
- 可能需要回溯,依赖于连接的类型
sort R, S on join keys
cursor_R <- R_sorted, cursor_S <- S_sorted
while cursor_R and cursor_S:
if cursor_R > cursor_S:
increment cursor_S
if cursor_R < cursor_S:
increment cursor_R
elif cursor_R and cursor_S match:
emit
increment cursor_S
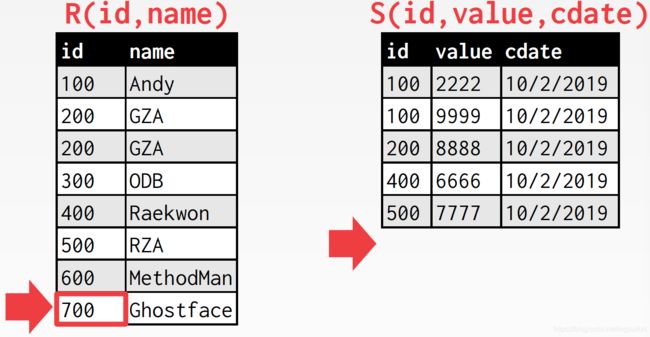
【例】
下面两张表,按照id进行连接,已排好序
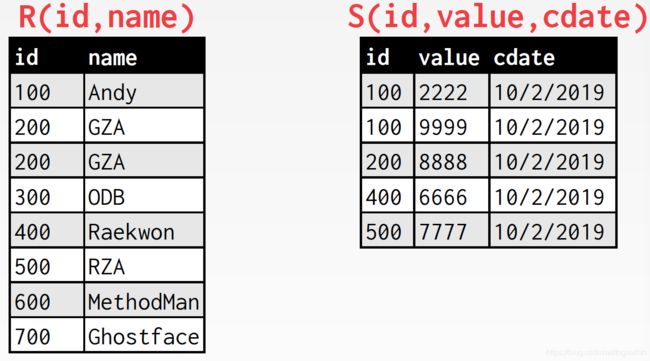
游标开始位置
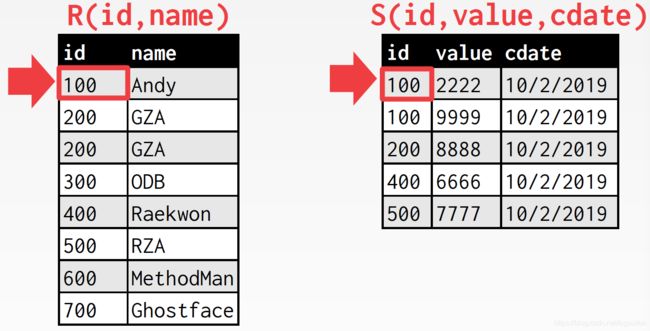
匹配上了,内表游标下移
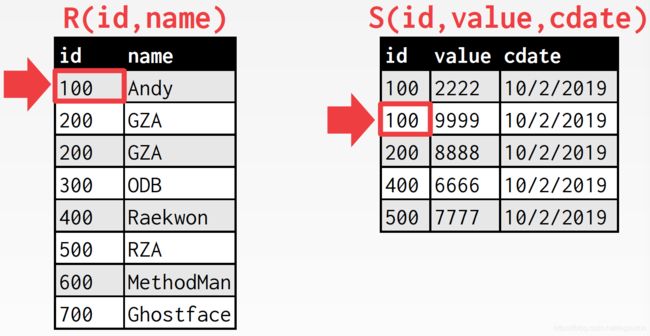
再一次匹配上了,继续下移
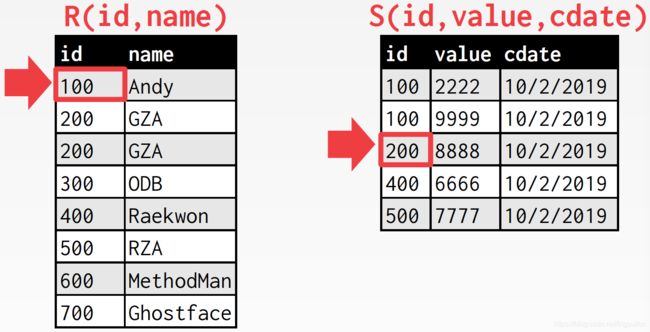
没匹配上,外表游标下移
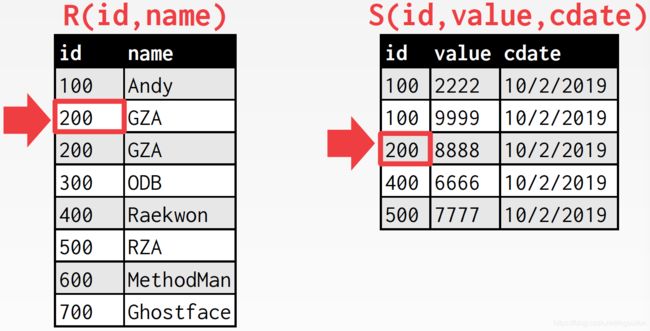
匹配上了,内表游标下移
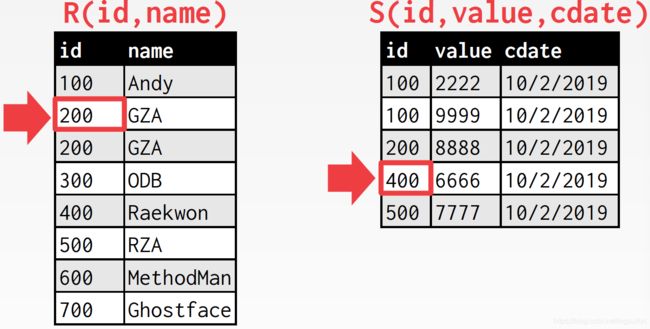
没匹配上,外表游标下移
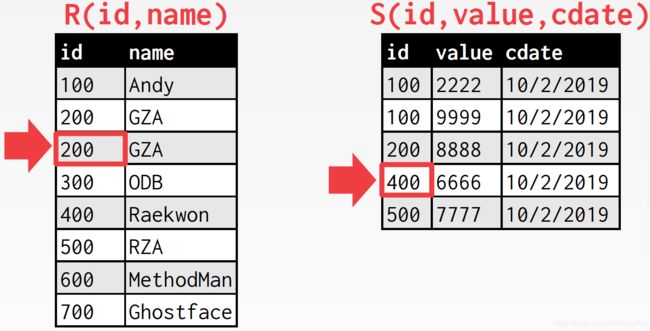
此时,外表游标指向的id小于内表游标指向的id,但却仍是200,应该与S表中id为200的tuple进行匹配,如果外表游标继续往下走,将会错过这些匹配,内表游标必须回溯到上一个id值的开始位置,因此我们需要维护这个信息
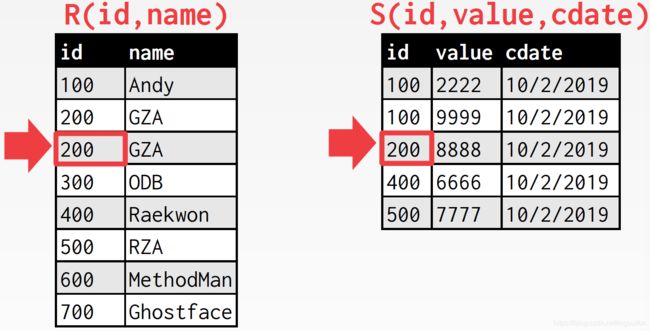
回溯,匹配后,内表游标下移
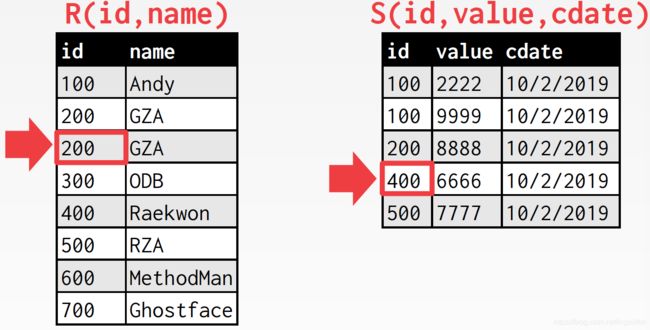
不匹配,外表游标下移
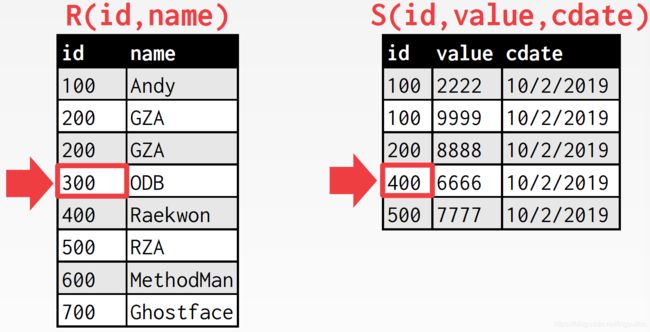
继续下移
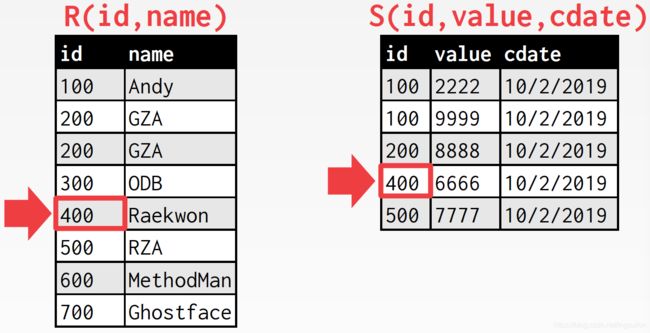
匹配上了,内表游标下移
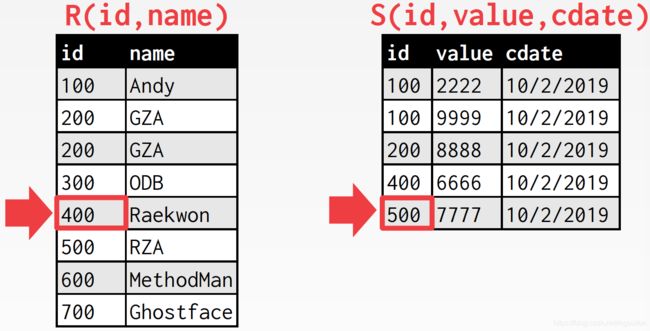
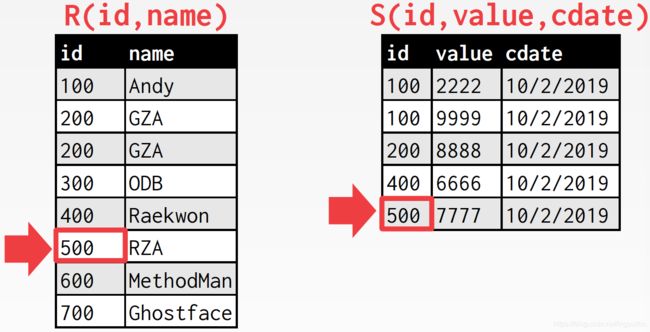
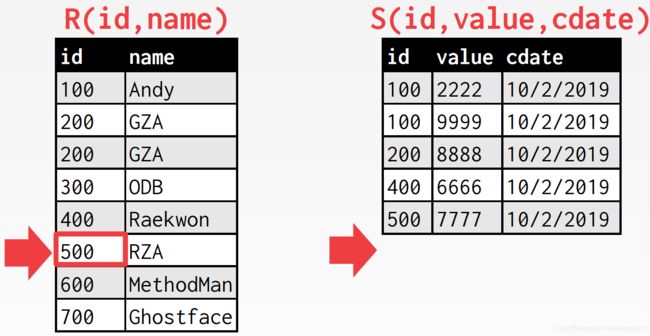
这里的要点还是在于,后面会不会还有id为500的tuple,如果有的话,内表游标还需要回溯
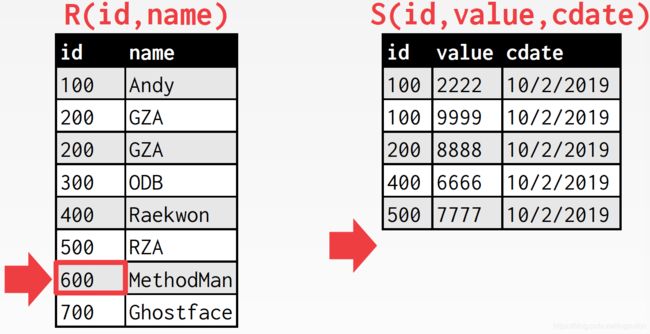
开销
排序开销(R): 2 M ⋅ ( 1 + ⌈ l o g B − 1 ⌈ M / B ⌉ ⌉ ) 2M\cdot(1+⌈log_{B-1}⌈M/B⌉⌉) 2M⋅(1+⌈logB−1⌈M/B⌉⌉)
排序开销(S): 2 N ⋅ ( 1 + ⌈ l o g B − 1 ⌈ N / B ⌉ ⌉ ) 2N\cdot(1+⌈log_{B-1}⌈N/B⌉⌉) 2N⋅(1+⌈logB−1⌈N/B⌉⌉)
归并开销:(M + N)
总开销:排序 + 归并
[例]一个数据库:
- 表R:M = 1000, m = 100,000
- 表S:N = 500, n = 40,000
在有100个缓冲页(本文中提到的块、页、block、page含义相同)的情况下,R和S的排序均需要两躺:
- 排序开销(R):2000 * (log 1000 / log 100) = 3000 IOs
- 排序开销(S):1000 * (log 500 / log 100) = 1350 IOs
- 合并开销 = (1000 + 500) = 1500 IOs
- 总开销 = 3000 + 1350 + 1500 = 5850 IOs
- 0.1ms/IO,总时间 ≈ 0.59 seconds
排序合并连接的最坏情况
合并阶段最坏的情况是两个关系中所有元组的连接属性包含相同的值。比如S表的id全部为1,而我们还去对S表按id排序。
开销:(M * N) + (排序开销)
什么时候排序合并连接有用?
- 一个或两个表已经按照连接的属性排序。
- 我们希望结果是排好序的,例如当查询语句出现order by的条件时。
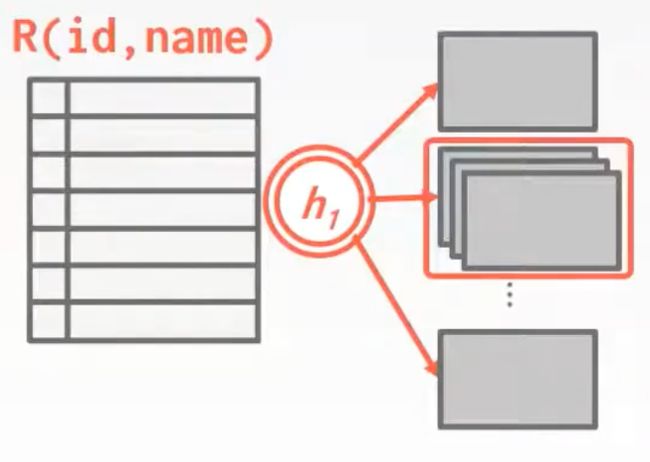
哈希连接
如果元组r ∈ R和s ∈ S满足连接条件,那么它们含有相同的连接属性值。
如果那个值被散列到一个部分 i,那么R的元组必然在 r i r_i ri 中并且S的元组必然在 s i s_i si 中。
因此,R在 r i r_i ri 中的tuples只需要与S在 s i s_i si 中的tuples比较。
两个阶段
阶段一:构建
- 扫描外表并在连接属性上使用哈希函数 h 1 h_1 h1 填充哈希表
阶段二:探测
- 扫描内表并对每个元组使用 h 1 h_1 h1 ,以跳转到哈希表中的某个位置并找到匹配的元组
build hash table HT_R for R
foreach tuple s ∈ S
output, if h_1(s) ∈ HT_R
Key: 查询连接表的属性
Value:因实现而异,取决于查询计划(查询树)中连接运算符上面的运算符期望得到的输入
哈希表存储的值
方法一:完整的Tuple
- 避免在匹配中检索外表元组的内容(避免IO)
- 占用更多的内存空间
方法二:Tuple ID
- 非常适合列式存储,因为DBMS不会从磁盘中获取它不需要的数据
- 如果连接的选择性低也会更好
布隆过滤器
用于集合成员资格查询(set membership query)的概率数据结构(bitmap)。
- 不会出现假阴性(如果查询目标存在,它不会回答你不存在)
- 有时会出现假阳性(如果查询目标不存在,它可能会回答你存在)
我们能使用布隆过滤器进行的操作:
Insert(x):
- 使用k个哈希函数将过滤器中x的散列值对应的位设置为1
Lookup(x):
- 检查每个哈希函数计算x得到的散列值对应的位是否都为1
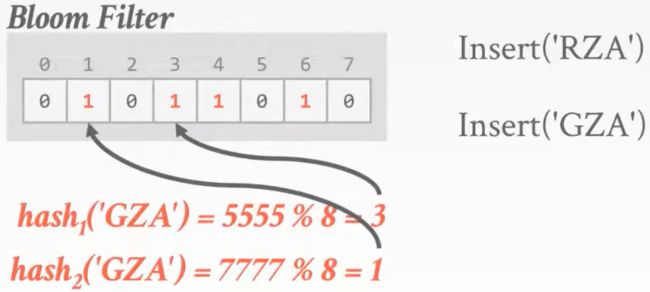
示例
如图,为一个布隆过滤器,由8位构成。

插入key,哈希函数数量k = 2

得到哈希值并进行模运算后,将相应位置1
类似的,再插入另一个key
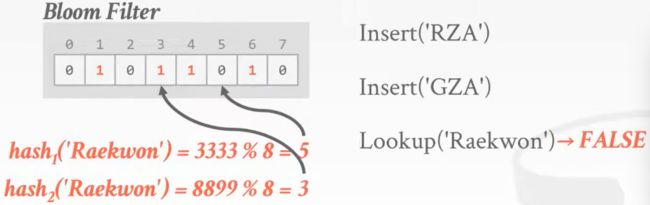
查询key,计算哈希值,检索过滤器上相应的位,此时得到的位不全为1,结果表明这个key不在哈希表中,因为无假阴性,所以结果可信
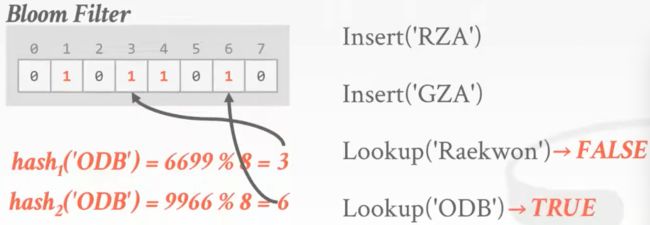
再查询另一个key,这一次我们得到的位都是1,结果表明该key存在于哈希表中,但事实上,这两个位上的1分别来自‘RZA’和‘GZA’,这样的结果就是假阳性的,因此这个结果不可信
探测阶段的优化
当key可能不在哈希表中时,可以在构建阶段创建布隆过滤器。
- 线程在探测哈希表之前检查过滤器。因为过滤器在CPU缓存中工作,所以这会很快。
- 有时称为横向消息传递。
在连接操作上执行布隆过滤,内表的元组只有在连接属性经散列后得到的每一位都是1才去哈希表中进行实际的匹配。
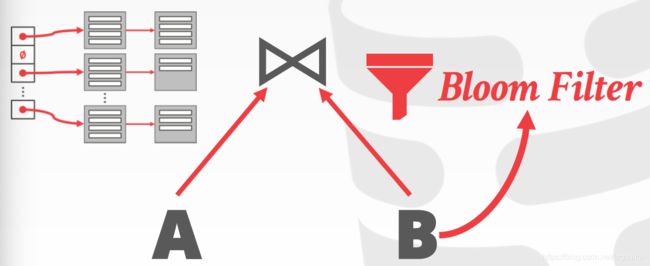
布隆过滤器在分布式数据库中十分有用,例如,当A、B分别为两台服务器或数据中心时,要执行连接操作,与其通过发送网络消息来执行探测阶段,不如把大小为几kb的布隆过滤器发送给其他机器,这样一来,在发送网络消息前,可以先在本地进行过滤。
之所以称它为横向消息传递,是因为它把查询操作执行的模型给拆分了,原本每个子节点通过单独的信道向父节点传递数据,不在兄弟节点间传递数据,但现在打破了这个模型。尽管违反了规则,但对我们却大有裨益。
无法在内存中处理的哈希连接
如果没有足够的内存来容纳整个哈希表,会发生什么?
我们不想让缓冲池管理器随机交换哈希表页。
Grace哈希连接
当表不能完全放在内存中时的哈希连接。
- 构建阶段: 将两个表的连接属性散列到分区中
- 探测阶段: 比较两个表对应分区中的元组
在前面的哈希连接中,只对外表构建哈希表,而对内表只进行检索是否有符合连接条件的元组,然后再连接。在Grace哈希连接中,对它们分别构建哈希表,然后对两边表中相应的分区进行嵌套循环连接。
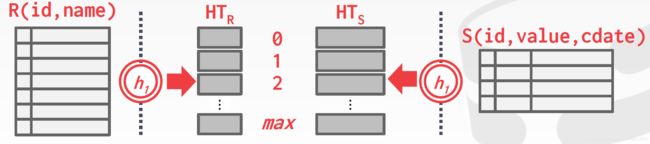
将R散列到不同的桶中(0,1,…,max)
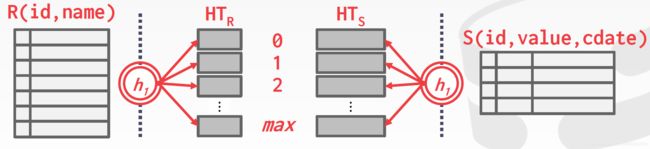
用相同的哈希函数对S进行散列
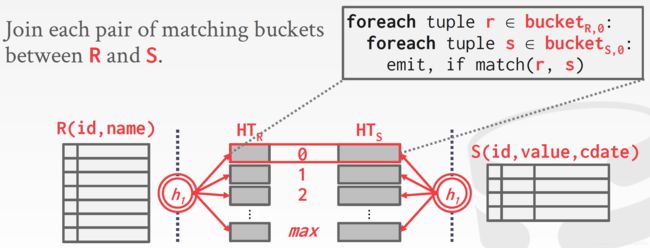
如果连接的属性重复值太多(很多元组都被散列到同一个分区中),那么桶链会越来越长,没办法都放在内存中时,可以使用递归分区将表拆分为更小的块
- 使用哈希函数h2(h2 ≠ h1)为 b u c k e t R , i bucket_{R,i} bucketR,i构建另一个哈希表
- 然后用另一个表相应的bucket的每个元组探测它
这时,可以用另一个哈希函数再分区
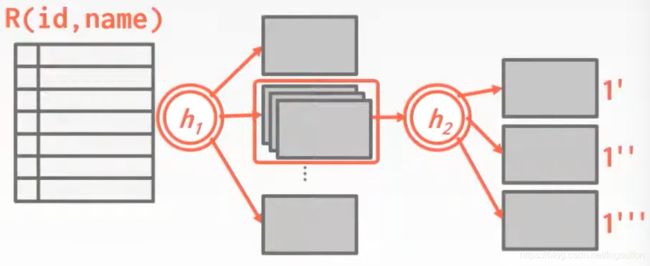
当进行连接时,在S表中经h1散列出的分区会和R表
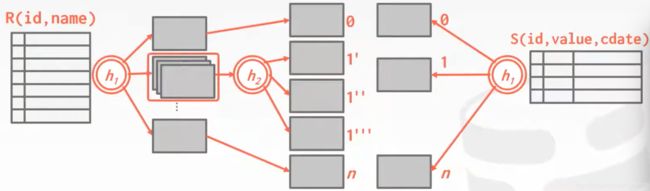
此时,会知道该分区已被拆分,所以进而使用h2进行散列
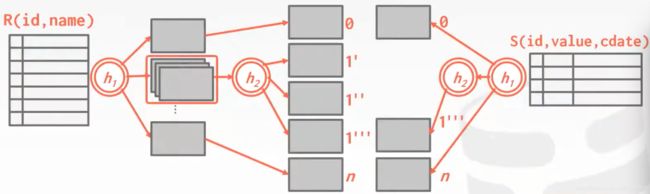
开销
假设我们有足够的缓冲块:
开销:3(M + N)
分区阶段:
- 读+写两个表
- 2(M + N) IOs
探测阶段:
- 读两个表
- M + N IOs
[例]一个数据库:
- M = 1000, m = 100,000
- M = 500, m = 40,000
开销分析:
- 3 * (M + N) = 3 * (1000 + 500) = 4500 IOs
- 0.1ms/IO,总时间 ≈ 0.45 seconds
总结
如果DBMS知道外表的大小,那么它可以使用静态哈希表。
- 构建/探测的计算开销更少操作
如果不知道大小,则必须使用动态哈希表或允许溢出页。
连接算法:总结
| 算法 | IO开销 | 例子 |
|---|---|---|
| 简单的嵌套循环连接 | M + (m * N) | 1.3 hours |
| 块嵌套循环连接 | M + (M * N) | 50 seconds |
| 使用索引的嵌套循环连接 | M + (m * C) | 可变 |
| 排序合并连接 | M + N + (sort cost) | 0.59 seconds |
| 哈希连接 | 3(M + N) | 0.45 seconds |
结论
除非数据已经排序,否则哈希几乎总是比排序更好。
注意事项
- 排序对非均匀数据更好
- 当结果需要排序时,排序更好
好的数据库管理系统使用其中一个或两个。