数据结构学习记录——图-最短路径问题(无权图单源最短路径算法、有权图单源最短路径算法、多源最短路径算法、Dijkstra(迪杰斯特拉)算法、Floyd算法)
目录
问题分类
无权图单源最短路径算法
思路
伪代码
时间复杂度
代码实现(C语言)
有权图单源最短路径算法
Dijkstra(迪杰斯特拉)算法
伪代码
时间复杂度
代码实现(C语言)
多源最短路径算法
两种方法
Floyd算法
代码实现(C语言)
问题分类
最短路径问题的抽象
在网络中,求两个不同顶点之间的所有路径中,边的权值之和最小的那一条路径
- 这条路径就是两点之间的最短路径(Shortest Path)
- 第一个顶点为源点(Source)
- 最后一个顶点为终点(Destination)
单源最短路径问题
从某固定源点出发,求其到所有其他顶点的最短路径。
- (有向)无权图
- (有向)有权图
多源最短路径问题
求任意两顶点间的最短路径
无权图单源最短路径算法
思路
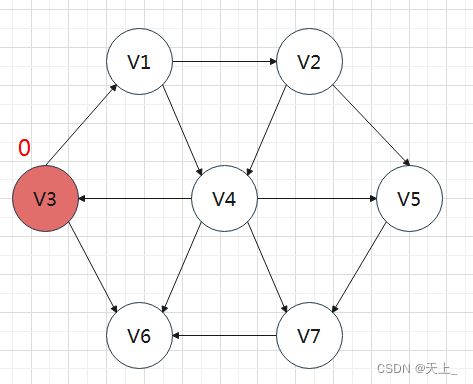
按照递增的顺序找出源点到各个顶点的最短路
在这样的一个图中,先访问与源点距离为1的顶点:
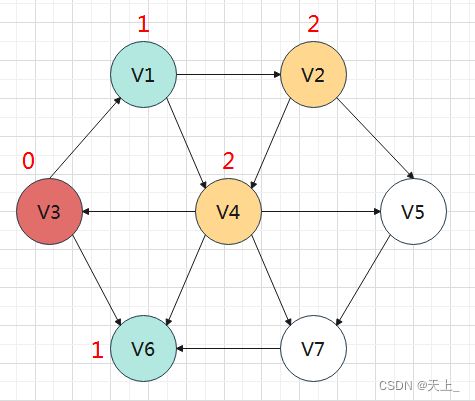
接着去访问与源点距离为2的顶点:
最后访问与源点距离为3的顶点,就发现所有顶点都已经被访问过了:
这样的方式我们发现与BFS(广度优先搜索)类似,所以通过改动原本BFS的算法来实现。
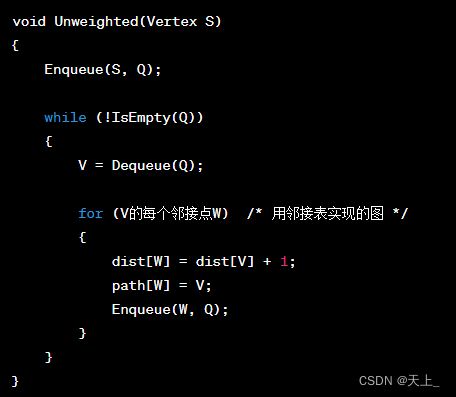
伪代码
与之前学习的BFS算法不一样的是,删去了visited数组,不再用这个来表示顶点是否被访问了;
而是添加了dist数组和path数组,
dist数组用于存储从起始顶点到每个顶点的最短路径长度。
在算法开始时,将所有顶点的初始距离设为-1(或者无穷大,一个足够大的值)来表示尚未计算出最短路径。
在算法执行过程中,每当找到一个更短的路径时,就会更新dist数组中对应顶点的值。
path数组用于存储从起始顶点到每个顶点的最短路径的前驱节点(即上一个节点)。
通过path数组,我们可以在搜索结束后从目标顶点回溯并恢复整个最短路径。(因为是反序所以可以利用堆栈来输出整个最短路径)
将顶点W的距离(即最短路径长度)更新为顶点V的距离加1。
这意味着通过顶点V可以到达顶点W,且路径长度比当前已知的最短路径长度更短。
更新顶点W的前驱节点为顶点V。这就帮助我们在找到最短路径后回溯并恢复整个路径。
时间复杂度
O(V + E)
其中 V 是顶点数,E 是边数。
- 遍历每个顶点:O(V)
- 对于每个顶点,访问其所有邻接顶点:O(E)
我们遍历了每个顶点一次,并且对于每个顶点,我们只访问了它的邻接顶点一次。
因此,该算法的时间复杂度为 O(V + E)。
注意:这个时间复杂度假设图的表示方式为邻接表,其中访问每个顶点的邻接顶点的时间复杂度为 O(1)。如果使用邻接矩阵表示图,那么访问每个顶点的邻接顶点的时间复杂度将变为 O(V),总的时间复杂度将变为 O(V^2)。
代码实现(C语言)
/*
邻接表存储 - 无权图的单源最短路算法
输入:图Graph,距离数组dist[],路径数组path[],源点S
输出:dist[]中记录了源点S到各顶点的最短距离,path[]中记录了最短路径的前驱顶点
dist[]和path[]全部初始化为-1
*/
void Unweighted(LGraph Graph, int dist[], int path[], Vertex S)
{
Queue Q; // 定义队列Q,用于广度优先搜索
Vertex V; // 当前顶点V
PtrToAdjVNode W; // 指向当前顶点V的邻接点的指针W
Q = CreateQueue(Graph->Nv); // 创建空队列Q,最大容量为图的顶点数Nv
dist[S] = 0; // 初始化源点S的距离为0
AddQ(Q, S); // 将源点S入队
while (!IsEmpty(Q))
{
V = DeleteQ(Q); // 从队列Q中删除一个顶点V,作为当前顶点
for (W = Graph->G[V].FirstEdge; W; W = W->Next)
{
/* 对V的每个邻接点W->AdjV */
if (dist[W->AdjV] == -1)
{
/* 若W->AdjV未被访问过 */
dist[W->AdjV] = dist[V] + 1; // 更新W->AdjV到源点S的距离
path[W->AdjV] = V; // 将当前顶点V记录在S到W->AdjV的路径上
AddQ(Q, W->AdjV); // 将W->AdjV入队,继续广度优先搜索
}
}
} /* while结束*/
}
有权图单源最短路径算法
Dijkstra(迪杰斯特拉)算法
- 令S = {源点s + 已经确定了最短路径的顶点
 }
} - 对任一未收录的顶点v,定义dist[v]为s到v的最短路径长度,但该路径仅经过S中的顶点。即路径
 的最小长度
的最小长度 - 该路径是按照递增的顺序生成的,则
1.真正的最短路必须只经过S中的顶点。
2.每次从未收录的顶点中选一个dist最小的收录(贪心算法)。
3.增加一个v进入S,可能影响另外一个w的dist值
对于第1点:
在算法的每一步,我们将一个顶点加入集合S,该顶点是在当前阶段中距离源点s的最短路径长度最小的顶点。由于我们每次只选择当前最短路径的顶点,所以可以确保这些顶点经过的路径是当前阶段中最短的路径。
对于第3点:
如果收录v使得s到w的路径变短,则s到w的路径一定经过v,并且v到w有一条边。
在每一步中,选择的顶点v是当前阶段中距离源点s最近的顶点,而且该距离是经过已确定最短路径顶点集合S的路径长度。
当将顶点v加入集合S后,我们更新其他顶点的dist值,以反映新的最短路径长度。如果从v到w之间不存在直接的边,那么根据Dijkstra算法的贪心策略,顶点w将不会被更新为新的最短路径。
所以是一定存在一条从v到顶点w的边,并且通过v的路径长度加上边的权重小于w当前的dist值,那么说明我们可以通过顶点v找到一条更短的路径来达到顶点w。因此,为了保证选择的是下一个最近的顶点,我们要先进行比较。即当前的dist值与通过v的路径长度加上边的权重比较。
![]()
伪代码
E
时间复杂度
邻接矩阵表示法
在使用邻接矩阵表示图的情况下,每次查找未收录顶点中dist最小者的时间复杂度为O(V),并且需要进行V次这样的查找。
在每次查找中,还需要遍历当前顶点的所有邻接顶点,即总共需要进行V次遍历。
因此,总的时间复杂度为O(V^2 + E)。
邻接表表示法
而在使用邻接表表示图的情况下,可以使用最小堆来查找未收录顶点中dist最小者,可以将时间复杂度降低到O(logV)。
在每次查找中,仅需遍历当前顶点的邻接表,即遍历的次数不会超过图中的边数E。因此,总的时间复杂度为O((V + E)logV)。
注意:在稀疏图(边的数量相对较少)的情况下,邻接表表示图的效率更高。而在稠密图(边的数量接近顶点数量的平方)的情况下,邻接矩阵表示图的效率更高。
代码实现(C语言)
/*
邻接矩阵存储 - 有权图的单源最短路算法
输入:图Graph,距离数组dist[],路径数组path[],源点S
输出:dist[]中记录了源点S到各顶点的最短距离,path[]中记录了最短路径的前驱顶点
使用邻接矩阵表示图,INFINITY表示不存在的边
*/
Vertex FindMinDist(MGraph Graph, int dist[], int collected[])
{
/* 返回未被收录顶点中dist最小者 */
Vertex MinV, V;
int MinDist = INFINITY;
for (V = 0; V < Graph->Nv; V++)
{
if (collected[V] == false && dist[V] < MinDist)
{
/* 若V未被收录,且dist[V]更小 */
MinDist = dist[V]; /* 更新最小距离 */
MinV = V; /* 更新对应顶点 */
}
}
if (MinDist < INFINITY) /* 若找到最小dist */
return MinV; /* 返回对应的顶点下标 */
else
return ERROR; /* 若这样的顶点不存在,返回错误标记 */
}
bool Dijkstra(MGraph Graph, int dist[], int path[], Vertex S)
{
int collected[MaxVertexNum];
Vertex V, W;
/* 初始化:此处默认邻接矩阵中不存在的边用INFINITY表示 */
for (V = 0; V < Graph->Nv; V++)
{
dist[V] = Graph->G[S][V];
if (dist[V] < INFINITY)
path[V] = S;
else
path[V] = -1;
collected[V] = false;
}
/* 先将起点收入集合 */
dist[S] = 0;
collected[S] = true;
while (1)
{
/* V = 未被收录顶点中dist最小者 */
V = FindMinDist(Graph, dist, collected);
if (V == ERROR) /* 若这样的V不存在 */
break; /* 算法结束 */
collected[V] = true; /* 收录V */
for (W = 0; W < Graph->Nv; W++) /* 对图中的每个顶点W */
{
/* 若W是V的邻接点并且未被收录 */
if (collected[W] == false && Graph->G[V][W] < INFINITY)
{
if (Graph->G[V][W] < 0) /* 若有负边 */
return false; /* 不能正确解决,返回错误标记 */
/* 若收录V使得dist[W]变小 */
if (dist[V] + Graph->G[V][W] < dist[W])
{
dist[W] = dist[V] + Graph->G[V][W]; /* 更新dist[W] */
path[W] = V; /* 更新S到W的路径 */
}
}
}
} /* while结束*/
return true; /* 算法执行完毕,返回正确标记 */
}
多源最短路径算法
两种方法
- 方法1:直接将单元最短路算法调用V遍
在稀疏图的情况下,单源最短路径算法时间复杂度为O(V^2 + E);
现在是多源,要调用V遍,故而时间复杂度T为:O(V^3 + E*V)
- 方法2:Floyd算法
这个算法用于稠密图,时间复杂度T直接就为:O(V^3)
在下面进行解释:
Floyd算法
对于稠密图的话,我们通常是可以使用邻接矩阵来表示图的,Floyd算法也是基于邻接矩阵的一个算法。
![D^{k}[i][j]](http://img.e-com-net.com/image/info8/9d6e06f632b64b628b4ab70f06c77067.png) = 路径
= 路径 的最小长度
的最小长度![D^{0},D^{1},......,D^{\left | V \right |-1}[i][j]](http://img.e-com-net.com/image/info8/f2ac987a70324dbeb19dff52a1ea37a2.png) ,即给出了i到j的真正最短距离
,即给出了i到j的真正最短距离 ,即初始的矩阵定义为:带权的邻接矩阵,对角元为0.表示结点到自身的距离为0
,即初始的矩阵定义为:带权的邻接矩阵,对角元为0.表示结点到自身的距离为0- 当
 已经完成,递推到
已经完成,递推到 时:
时:
最短路径
时,
=
。
最短路径
时,该路径必定由两段最短路径组成:
Floyd算法也是逐步地求出最短距离的,通过遍历所有可能的中间节点k,并不断尝试更新D[i][j]的值,Floyd算法逐步优化路径长度,最终找到图中所有节点对之间的最短路径。
假设我们有一个图,其中有节点i和节点j需要连接,并且我们已经知道了节点i到节点j的当前最短路径长度(存储在D[i][j]中)。
现在,我们引入一个中间节点k,想要通过节点k来尝试找到更短的路径,即尝试在节点i和节点j之间建立一条路径,其中包括节点k。
我们首先考虑从节点i到节点k的路径长度,这个距离我们可以在D数组中找到,即D[i][k]。接着,我们考虑从节点k到节点j的路径长度,同样可以在D数组中找到,即D[k][j]。
现在,我们将这两段路径长度加在一起,得到D[i][k] + D[k][j]。这个值表示通过节点k连接的从节点i到节点j的路径长度。
接下来,我们将这个通过节点k的路径长度与当前已知的最短路径长度(即D[i][j])进行比较。
- 如果通过节点k的路径长度更短,那么我们更新D[i][j]的值为D[i][k] + D[k][j],表示我们找到了一条经过节点k的更短路径。
- 如果通过节点k的路径长度并不比当前已知的最短路径长度更短,那么我们不做任何更改,保持D[i][j]不变。
代码实现(C语言)
/* 邻接矩阵存储 - 多源最短路算法 */
bool Floyd(MGraph Graph, WeightType D[][MaxVertexNum], Vertex path[][MaxVertexNum])
{
Vertex i, j, k;
/* 初始化 */
for (i = 0; i < Graph->Nv; i++)
{
for (j = 0; j < Graph->Nv; j++)
{
D[i][j] = Graph->G[i][j]; // 初始化最短路径数组D为图的邻接矩阵
path[i][j] = -1; // 初始化路径数组path为-1,表示当前节点间没有中间节点
}
}
for (k = 0; k < Graph->Nv; k++)
{
for (i = 0; i < Graph->Nv; i++)
{
for (j = 0; j < Graph->Nv; j++)
{
if (D[i][k] + D[k][j] < D[i][j])
{ // 如果通过中间节点k可以获得更短的路径
D[i][j] = D[i][k] + D[k][j]; // 更新节点i到节点j的最短路径长度
if (i == j && D[i][j] < 0)
{ // 若发现负值圈,即存在权重之和为负的回路
return false; // 不能正确解决,返回错误标记
}
path[i][j] = k; // 更新节点i到节点j的路径经过的中间节点为k
}
}
}
}
return true; // 算法执行完毕,返回正确标记
}
end
学习自:MOOC数据结构——陈越、何钦铭