【机器学习】Decision Tree 决策树算法详解 + Python代码实战

---

一、直观理解决策树

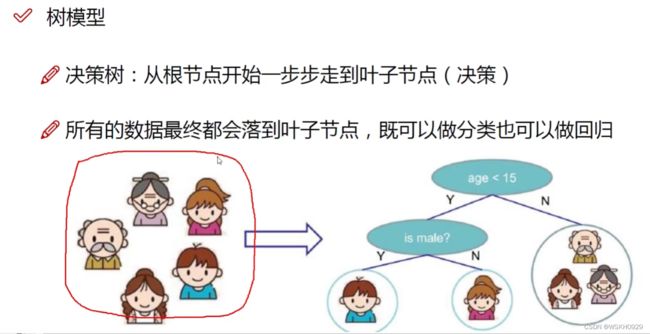
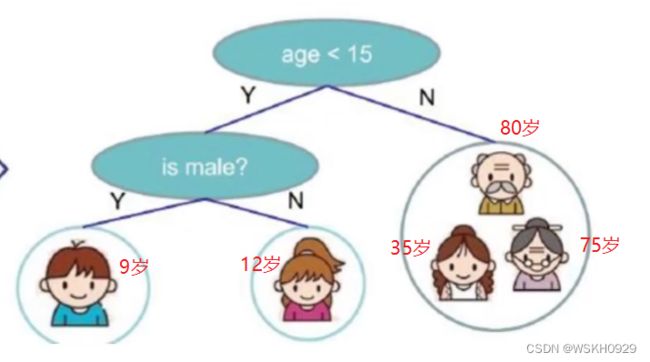
决策树即通过一步步决策得到最终结果的树

如下图所示，如果要判断一个人在家庭里的身份，我们可以先判断ta年龄是否大于15，如果是，则说明ta是爷爷或奶奶或妈妈，如果不是，则再判断ta是否为男性，如果是，则ta是儿子，否则ta是女儿。

这就是一个决策树的基本流程。


训练阶段（构造决策树）：

• 确定根节点的特征判断
• 然后从根节点的往下分支，继续确定子节点的特征判断

测试阶段：根据训练出来的决策树从根节点往下走一遍就完事了

二、熵的作用

通过上面的讲解，我们肯定会疑惑，训练过程中根节点怎么选择用哪个特征进行判断呢？接下来的子节点又怎么选择呢？

答：选择分类效果最强的

但是，怎么评判一个特征的分类效果强还是不强呢？下面我们就介绍一个衡量标准：熵

简单理解：熵就是混乱程度

如：杂货铺卖的东西种类很多，可以说你去购买其中某个物品的熵很大

问：我们希望节点分支后数据类别的熵值大还是小呢？
答：当然希望熵值小。如果分支完熵值还是很大，那说明其还是很混乱，分支就没有什么作用了（我们最终目的是分类，每个决策树的叶子节点熵值都是很小的，都是纯纯的某一类）

三、信息增益

当概率P=0.5时，熵最大，最不确定

当P=0或1时，熵值最小，最确定

我们希望通过某特征判断后，熵值的下降越大越好，即不确定性减少的程度越大越好，而这个不确定性减少的程度就被成为信息增益。我们一般希望特征判断后信息增益越大越好。

四、决策树构造实例

4.1 问题描述

有四个特征（天气、温度、湿度、有无风），和一个标签（是否出去玩）

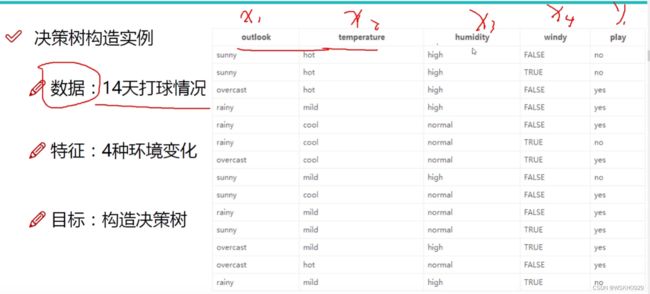
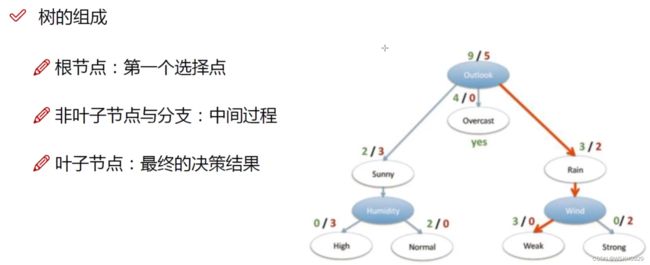
4.2 根节点构造

问题中有四个特征，故我们有4种构造根节点特征划分的方法。那我们怎么选择最好的特征划分呢？
前面说过了，看信息增益，选信息增益最大的特征划分构造根节点。

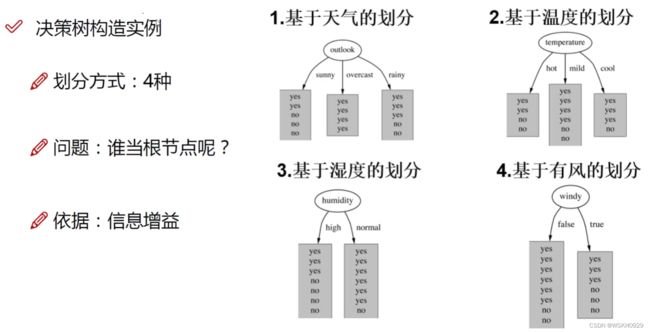
计算最开始没有进行特征划分时的数据的熵值：0.940

举例：基于天气的划分

计算完每个种类的熵值之后，不能直接对其进行求和，而是进行加权的求和（取每个种类的概率作为权值）

从上图可以得出，信息增益最大的是outlook（基于天气的划分），所以根节点就以outlook进行特征划分，后面每一个节点的构造也是类似的步骤。

五、信息增益率和GINI系数

5.1 信息增益存在的问题

用信息增益来选取特征划分的方法，不适用与存在一个特征的可选值很多的情况（如将唯一编号id作为特征，每一个样本的id都不一样，导致用ID来作为根节点特征划分时，熵值直接下降为0，此时的信息增益为最大，但实际我们知道，用编号ID来作为根节点的特征划分是毫无意义的）

5.2 信息增益率

信息增益率= 信息增益 / 自身的熵值

例如计算编号的自身熵值，样本量为14，每一条样本的ID不同，故其概率 P = $\frac{1}{14}$ ，根据熵值的计算公式可得，编号的自身熵值为：
$$编号的自身熵=14\cdot \left(-\frac{1}{14}\cdot {\log }_2\left(\frac{1}{14}\right)\right)=3.8074$$

再计算信息增益：
$$原始熵值=-\frac{5}{14}{\log }_2\left(\frac{5}{14}\right)-\frac{9}{14}{\log }_2\left(\frac{9}{14}\right)=0.9403$$
由于以ID进行特征划分后的熵值为0，故信息增益为：
$$信息增益=原始熵值-0=0.9403$$
综上，信息增益率为：
$$信息增益率=\frac{0.9403}{3.8074}=0.247$$
同样的方法计算OutLook的信息增益率为0.2864，这样就避免了使用ID进行特征划分的情况。

显然利用信息增益率可以屏蔽掉类似ID类别过多的问题。

5.3 GINI系数

GINI系数的计算公式如下：
$$\mathrm{Gini}(p)=\sum _{k=1}^K{p}_k\left(1-p_k\right)=1-\sum _{k=1}^K{p}_k^2$$

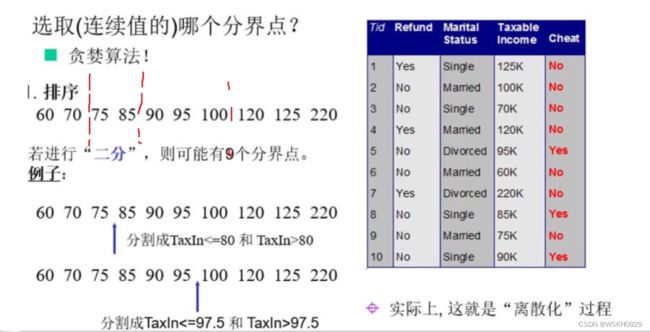
六、连续值特征划分

1. 先对连续值特征进行升序排列
2. 以每两个相邻值的中间值进行特征划分，以下图为例，共有9种划分方式
   

七、剪枝方法（预剪枝和后剪枝）

剪枝的目的：缓解过拟合

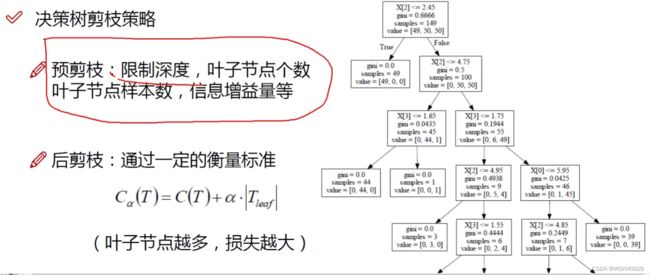
预剪枝：边建立决策树边剪枝（更实用）

• 限制树深度：相当于限制从根节点到叶子节点用来划分的特征个数
• 限制叶子节点个数：设置决策树最末端的最大节点数（末端节点即叶子节点）
• 限制叶子节点样本数：每个节点的最小样本数
• 限制信息增益量：如果按照某特征进行划分后，信息增益量小于一个阈值，则不进行该特征划分

后剪枝：建立完决策树后再进行剪枝操作

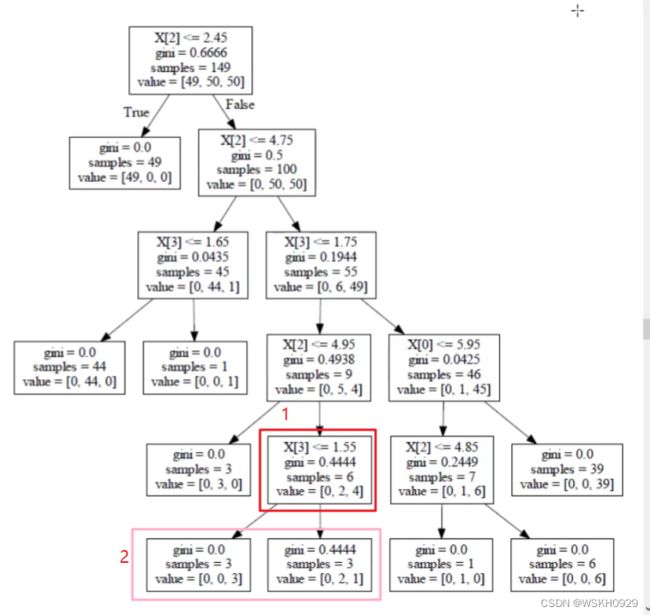
后剪枝的例子：
以下图的1处分支产生2处为例，按照公式计算1处的损失：
$$1处的损失=0.4444\ast 6+\alpha$$
$$2处的损失=0\ast 3+0.4444\ast 3+2\alpha$$

如果1处的损失小于2处的损失，则不应该进行分支，对1处进行后剪枝。

其中 $\alpha$ 是个参数，我们可以对其进行设置，其越大，越难进行分支，就越不容易过拟合（但可能导致欠拟合）

八、回归问题预测思路

如下所示，在回归问题中，右边叶子节点的输出等于该叶子节点中样本特征的平均值：
$$右边叶子节点的预测值=\frac{80+75+35}{3}=\frac{190}{3}=63.3333$$

九、Python代码实现决策树

9.1 导入所需要的库

# 导入所需要的库
import math

9.2 构建数据集

# 创建数据
def createDataSet():
    # 数据
    dataSet = [
        [0, 0, 0, 0, 'no'],
        [0, 0, 0, 1, 'no'],
        [0, 1, 0, 1, 'yes'],
        [0, 1, 1, 0, 'yes'],
        [0, 0, 0, 0, 'no'],
        [1, 0, 0, 0, 'no'],
        [1, 0, 0, 1, 'no'],
        [1, 1, 1, 1, 'yes'],
        [1, 0, 1, 2, 'yes'],
        [1, 0, 1, 2, 'yes'],
        [2, 0, 1, 2, 'yes'],
        [2, 0, 1, 1, 'yes'],
        [2, 1, 0, 1, 'yes'],
        [2, 1, 0, 2, 'yes'],
        [2, 0, 0, 0, 'no'],
    ]
    # 列名
    labels = ['F1-AGE', 'F2-WORK', 'F3-HOME', 'F4-LOAN']
    return dataSet, labels

9.3 函数编写

# 获取当前样本里最多的标签
def getMaxLabelByDataSet(curLabelList):
    classCount = {}
    maxKey, maxValue = None, None
    for label in curLabelList:
        if label in classCount.keys():
            classCount[label] += 1
            if maxValuex < classCount[label]:
                maxKey, maxValue = label, classCount[label]
        else:
            classCount[label] = 1
            if maxKey is None:
                maxKey, maxValue = label, 1
    return maxKey

# 计算熵值
def calcEntropy(dataSet):
    # 1. 获取所有样本数
    exampleNum = len(dataSet)
    # 2. 计算每个标签值的出现数量
    labelCount = {}
    for featVec in dataSet:
        curLabel = featVec[-1]
        if curLabel in labelCount.keys():
            labelCount[curLabel] += 1
        else:
            labelCount[curLabel] = 1
    # 3. 计算熵值(对每个类别求熵值求和)
    entropy = 0
    for key, value in labelCount.items():
        # 概率值
        p = labelCount[key] / exampleNum
        # 当前标签的熵值计算并追加
        curEntropy = -p * math.log(p, 2)
        entropy += curEntropy
    # 4. 返回
    return entropy

# 选择最好的特征进行分割，返回最好特征索引
def chooseBestFeatureToSplit(dataSet):
    # 1. 计算特征个数 -1 是减去最后一列标签列
    featureNum = len(dataSet[0]) - 1
    # 2. 计算当前（未特征划分时）熵值
    curEntropy = calcEntropy(dataSet)
    # 3. 找最好特征划分
    bestInfoGain = 0  # 最大信息增益
    bestFeatureIndex = -1  # 最好特征索引
    for i in range(featureNum):
        # 拿到当前列特征
        featList = [example[i] for example in dataSet]
        # 获取唯一值
        uniqueVals = set(featList)
        # 新熵值
        newEntropy = 0
        # 计算分支（不同特征划分）的熵值
        for val in uniqueVals:
            # 根据当前特征划分dataSet
            subDataSet = splitDataSet(dataSet, i, val)
            # 加权概率值
            weight = len(subDataSet) / len(dataSet)
            # 计算熵值，追加到新熵值中
            newEntropy += (calcEntropy(subDataSet) * weight)
        # 计算信息增益
        infoGain = curEntropy - newEntropy
        # 更新最大信息增益
        if bestInfoGain < infoGain:
            bestInfoGain = infoGain
            bestFeatureIndex = i
    # 4. 返回
    return bestFeatureIndex

# 根据当前选中的特征和唯一值去划分数据集
def splitDataSet(dataSet, featureIndex, value):
    returnDataSet = []
    for featVec in dataSet:
        if featVec[featureIndex] == value:
            # 将featureIndex那一列删除
            deleteFeatVec = featVec[:featureIndex]
            deleteFeatVec.extend(featVec[featureIndex + 1:])
            # 将删除后的样本追加到新的dataset中
            returnDataSet.append(deleteFeatVec)
    return returnDataSet

# 递归生成决策树节点
def createTreeNode(dataSet, labels, featLabels):
    # 取出当前节点的样本的标签 -1 表示在最后一位
    curLabelList = [example[-1] for example in dataSet]
    
    # -------------------- 停止条件 --------------------
    # 1. 判断当前节点的样本的标签是不是已经全为1个值了，如果是则直接返回其唯一类别
    if len(curLabelList) == curLabelList.count(curLabelList[0]):
        return curLabelList[0]
    # 2. 判断当前可划分的特征数是否为1，如果为1则直接返回当前样本里最多的标签
    if len(labels) == 1:
        return getMaxLabelByDataSet(curLabelList)
    
    # -------------------- 下面是正常选择特征划分的步骤 --------------------
    # 1. 选择最好的特征进行划分(返回值为索引)
    bestFeatIndex = chooseBestFeatureToSplit(dataSet)
    # 2. 利用索引获取真实值
    bestFeatLabel = labels[bestFeatIndex]
    # 3. 将特征划分加入当前决策树
    featLabels.append(bestFeatLabel)
    # 4. 构造当前节点
    myTree = {bestFeatLabel: {}}
    # 5. 删除被选择的特征
    del labels[bestFeatIndex]
    # 6. 获取当前最佳特征的那一列
    featValues = [example[bestFeatIndex] for example in dataSet]
    # 7. 去重(获取唯一值)
    uniqueFeaValues = set(featValues)
    # 8. 对每个唯一值进行分支
    for value in uniqueFeaValues:
        # 递归创建树
        myTree[bestFeatLabel][value] = createTreeNode(
            splitDataSet(dataSet, bestFeatIndex, value), labels.copy(),
            featLabels.copy())
    # 9. 返回
    return myTree

9.4 测试算法效果

# 测试一下！！！
# 1. 获取数据集
dataSet,labels = createDataSet()
# 2. 构建决策树
myDecisionTree = createTreeNode(dataSet,labels,[])
# 3. 输出
print(myDecisionTree)

输出：

{'F3-HOME': {0: {'F2-WORK': {0: 'no', 1: 'yes'}}, 1: 'yes'}}

十、SkLearn库实现决策树并可视化

10.1 Graphviz可视化库安装

进入下面网址
http://graphviz.gitlab.io/download/
点击右边菜单栏的Download按钮，然后选择一个版本进行下载（我选择了最新版的EXE格式的安装文件）

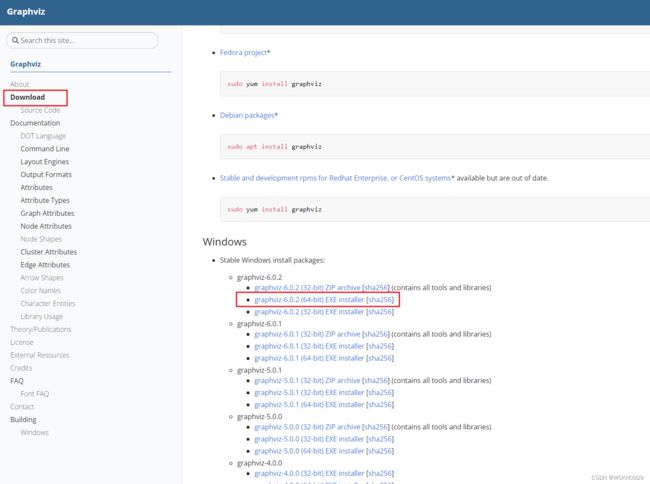
然后就是正常安装步骤即可

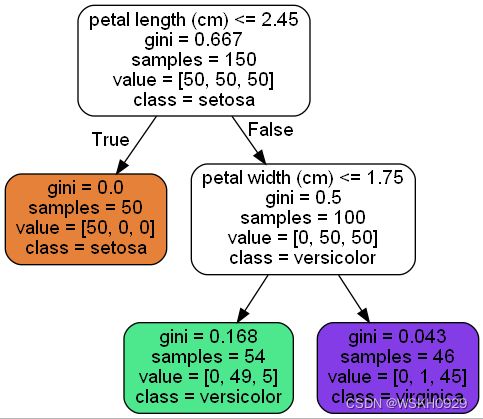
10.2 树模型的可视化展示

# 导入相关库
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz

# 加载数据集
iris = load_iris()
# 获取特征x和标签y
x = iris.data[:, 2:]
y = iris.target
# 创建决策树算法对象
tree_clf = DecisionTreeClassifier(max_depth=2)
# 构建决策树
tree_clf.fit(x, y)

# 导出.dot文件，为可视化做铺垫
export_graphviz(
    tree_clf,
    out_file='iris_tree.dot', # 输出文件路径
    feature_names=iris.feature_names[2:],
    class_names=iris.target_names,
    rounded=True,
    filled=True
)

获得.dot文件后，可以用下面的命令将其转化为png文件

dot -Tpng dot文件路径 -o 要输出的文件路径

例如：

dot -Tpng iris_tree.dot -o iris_tree.png

10.3 预剪枝参数及作用分析

10.3.1 预剪枝参数介绍

• min_samples_split：节点在分割之前必须具有的最小样本数
• min_samples_.leaf：叶子节点必须具有的最小样本数
• max_leaf_nodes：叶子节点的最大数量
• max_features：在每个节点处评估用于拆分的最大特征数（除非特征非常多，否则不建议限制最大特征数）
• max_depth：树最大的深度

10.3.2 预剪枝参数作用

预剪枝就是用来缓解过拟合的

下面让我们直观的感受一下预剪枝参数的作用：

首先，定义绘制决策边界的函数：

from matplotlib.colors import ListedColormap


def plot_decision_boundary(clf,
                           X,
                           y,
                           axes=[0, 7.5, 0, 3],
                           iris=True,
                           legend=False,
                           plot_training=True):
    x1s = np.linspace(axes[0], axes[1], 100)
    x2s = np.linspace(axes[2], axes[3], 100)
    x1, x2 = np.meshgrid(x1s, x2s)
    X_new = np.c_[x1.ravel(), x2.ravel()]
    y_pred = clf.predict(X_new).reshape(x1.shape)
    custom_cmap = ListedColormap(['#fafab0', '#9898ff', '#a0faa0'])
    plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)
    if not iris:
        custom_cmap2 = ListedColormap(['#7d7d58', '#4c4c7f', '#507d50'])
        plt.contour(x1, x2, y_pred, cmap=custom_cmap2, alpha=0.8)
    if plot_training:
        plt.plot(X[:, 0][y == 0], X[:, 1][y == 0], "yo", label="Iris-Setosa")
        plt.plot(X[:, 0][y == 1],
                 X[:, 1][y == 1],
                 "bs",
                 label="Iris-Versicolor")
        plt.plot(X[:, 0][y == 2], X[:, 1][y == 2], "g^", label="Iris-Virginica")
        plt.axis(axes)
    if iris:
        plt.xlabel("Petal length", fontsize=14)
        plt.ylabel("Petal width", fontsize=14)
    else:
        plt.xlabel(r"$x_1$", fontsize=18)
        plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
    if legend:
        plt.legend(loc="lower right", fontsize=14)

然后是测试代码：

from sklearn.datasets import make_moons
import matplotlib.pyplot as plt

X, y = make_moons(n_samples=100, noise=0.25, random_state=53)
tree_clf1 = DecisionTreeClassifier(random_state=42)
tree_clf2 = DecisionTreeClassifier(min_samples_leaf=4, random_state=42)

tree_clf1.fit(X, y)
tree_clf2.fit(X, y)

plt.figure(figsize=(12, 4))
plt.subplot(121)
plot_decision_boundary(tree_clf1, X, y, axes=[-1.5, 2.5, -1, 1.5], iris=False)
plt.title('No Restrictions')

plt.subplot(122)
plot_decision_boundary(tree_clf2, X, y, axes=[-1.5, 2.5, -1, 1.5], iris=False)
plt.title('min_samples_leaf = 4')

结果：

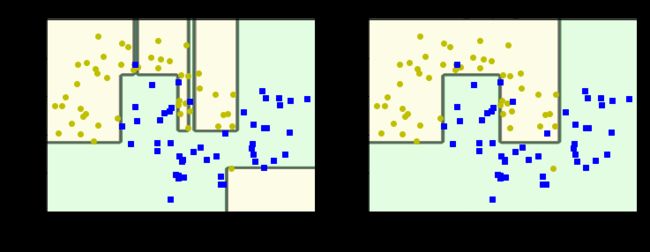
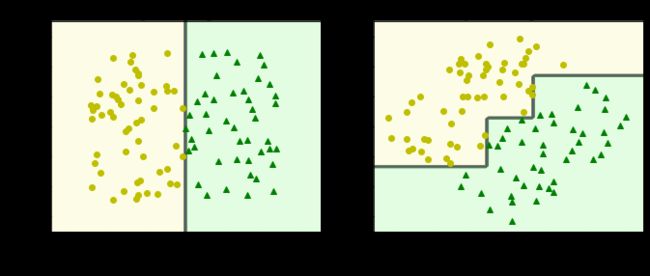
左边是没有增加预剪枝参数的决策边界，明显可以看出，它将一些离群点也考虑进去了，模型过为复杂，存在过拟合现象

而右边限制了 min_samples_leaf = 4 的决策树就没有存在明显的过拟合现象。

10.4 对数据的敏感性分析

先看左图，决策树很轻松的用一根垂直线将样本分成了两份，但如果我们对数据做一点小小的改动，将原本的数据进行90度旋转，如右图所示，决策边界就会复杂很多。

主要原因：决策树进行决策边界划分时只能沿着与坐标轴垂直的方向划分，所以对数据很敏感

可视化代码（plot_decision_boundary函数见10.3.2节）：

from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
import numpy as np

np.random.seed(6)
Xs = np.random.rand(100, 2) - 0.5
ys = (Xs[:, 0] > 0).astype(np.int32)*2
angle = np.pi / 4
rotation_matrix = np.array([[np.cos(angle), -np.sin(angle)],
                            [np.sin(angle), np.cos(angle)]])
Xsr = Xs.dot(rotation_matrix)

tree_clf_s = DecisionTreeClassifier(random_state=42)
tree_clf_s.fit(Xs, ys)

tree_clf_sr = DecisionTreeClassifier(random_state=42)
tree_clf_sr.fit(Xsr, ys)

plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_decision_boundary(tree_clf_s,
                       Xs,
                       ys,
                       axes=[-0.7, 0.7, -0.7, 0.7],
                       iris=False)
plt.title('Sensitivity to training set rotation')
plt.subplot(122)
plot_decision_boundary(tree_clf_sr,
                       Xsr,
                       ys,
                       axes=[-0.7, 0.7, -0.7, 0.7],
                       iris=False)
plt.title('Sensitivity to training set rotation')
plt.show()

10.5 回归任务

# 构建数据
np.random.seed(42)
m = 200
X = np.random.rand(m,1)
y = 4 * (X - 0.5)**2
y = y + np.random.randn(m,1) / 10
# 数据可视化
plt.plot(X,y,'go')
plt.show()

创建回归树对象并训练：

from sklearn.tree import DecisionTreeRegressor

# 创建回归树
tree_reg = DecisionTreeRegressor(max_depth=2)
# 训练回归树
tree_reg.fit(X, y)

用10.2节中的可视化方法将树模型可视化：
可以发现，在回归树中，判断分支好坏的指标是MSE（均方差），分支后的子节点均方差越小越好，代表分支后，子节点的样本都比较接近，分类效果较好

from sklearn.tree import DecisionTreeRegressor

tree_regl = DecisionTreeRegressor(random_state=42, max_depth=2)
tree_reg2 = DecisionTreeRegressor(random_state=42, max_depth=3)
tree_regl.fit(X, y)
tree_reg2.fit(X, y)


def plot_regression_predictions(tree_reg,
                                X,
                                y,
                                axes=[0, 1, -0.2, 1],
                                ylabel="$y$"):
    x1 = np.linspace(axes[0], axes[1], 500).reshape(-1, 1)
    y_pred = tree_reg.predict(x1)
    plt.axis(axes)
    plt.xlabel("$x_1$", fontsize=18)
    if ylabel:
        plt.ylabel(ylabel, fontsize=18, rotation=0)
    plt.plot(X, y, "b.")
    plt.plot(x1, y_pred, "r.-", linewidth=2, label=r"$\hat{y}$")


plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_regression_predictions(tree_regl, X, y)

for split, style in ((0.1973, "k-"), (0.0917, "k-"), (0.7718, "k-")):
    plt.plot([split, split], [-0.2, 1], style, linewidth=2)
plt.text(0.21, 0.65, "Depth=0", fontsize=15)
plt.text(0.01, 0.2, "Depth=1", fontsize=13)
plt.text(0.65, 0.8, "Depth=1", fontsize=13)
plt.legend(loc="upper center", fontsize=18)
plt.title("max_depth=2", fontsize=14)

plt.subplot(122)
plot_regression_predictions(tree_reg2,X,y,ylabel=None)
for split,style in ((0.1973,"k-"),(0.0917,"k-"),(0.7718,"k-")):
    plt.plot([split,split],[-0.2,1],style,linewidth=2)
for split in (0.0458,0.1298,0.2873,0.9040):
    plt.plot([split,split],[-0.2,1],"k:",linewidth=1)
plt.text(0.3,0.5,"Depth=2",fontsize=13)
plt.title("max_depth=3",fontsize=14)
plt.show ()

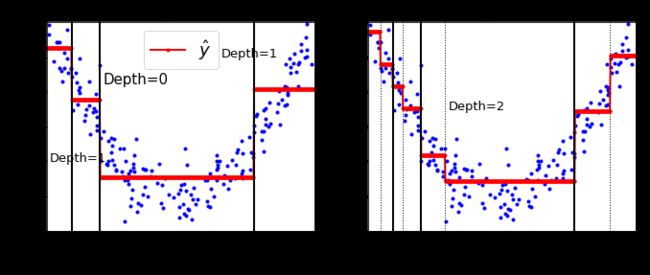
从下图可以看出，max_depth设置为3的模型较为复杂，max_depth设置为2的模型较为简单

让我们不限制回归树模型看看它能多复杂

tree_reg1 = DecisionTreeRegressor(random_state=42)
tree_reg2 = DecisionTreeRegressor(random_state=42, min_samples_leaf=10)
tree_reg1.fit(X, y)
tree_reg2.fit(X, y)
x1 = np.linspace(0, 1, 500).reshape(-1, 1)
y_pred1 = tree_reg1.predict(x1)
y_pred2 = tree_reg2.predict(x1)
plt.figure(figsize=(11, 4))
plt.subplot(121)
plt.plot(X, y, "b.")
plt.plot(x1, y_pred1, "r.-", linewidth=2, label=r"$\hat{y}$")
plt.axis([0, 1, -0.2, 1.1])
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", fontsize=18, rotation=0)
plt.legend(loc="upper center", fontsize=18)
plt.title("No restrictions", fontsize=14)

plt.subplot(122)
plt.plot(X,y,"b.")
plt.plot(x1,y_pred2,"r.-",linewidth=2,label=r"$\hat{y}$")
plt.axis([0,1,-0.2,1.1])
plt.xlabel("$x_1$",fontsize=18)
plt.title("min_samples_leaf=10".format (tree_reg2.min_samples_leaf),fontsize=14)
plt.show()

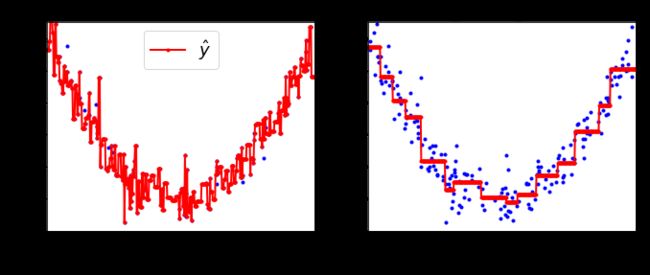
下图中可以看出，左边（不进行预剪枝）的回归树模型非常复杂，几乎拟合了所有点

右边限制了 min_samples_leaf=10 的回归树 就相对简单一些