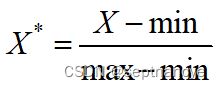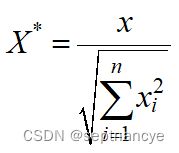Python数据预处理和PCA、ICA、LDA降维的方法(实验代码)

目录

1.标准差标准化

数据预处理——标准差标准化 

数据预处理——离差标准化

数据预处理——非线性转换 

数据预处理——归一化

数据预处理——二值化

数据预处理——独热编码

数据预处理——缺失值的插补

数据预处理——生成多项式特征

 2,降维

PCA

 ICA

 LDA

---

数据预处理——标准化

标准化是指将数据按比例缩放，并落入某个特定区间，目的是消除特征间量纲和取值范围差异的影响。

常用的标准化方法：标准差标准化和离差标准化。

1.标准差标准化

标准差标准化也称零均值标准化或分数标准化，是当前使用最广泛的数据标准化方法。经标准差标准化处理后的数据的标准差为1，均值为0，其转化公式如下公式所示。

 其中 X ̅为原始数据的均值， δ为原始数据的标准差。注意，这里的标准差是指加了Delta Degrees of Freedom因子后的标准差，这与传统的标准差计算公式有区别（在numpy中，有std()函数用于计算标准差）。

preprocessing模块的StandardScaler类可用于特征的标准差标准化处理。StandardScaler类能创建标准差标准化转换器，其基本语法格式如下。

class sklearn.preprocessing.StandardScaler(copy=True, with_mean=True, with_std=True)

StandardScaler类常用的参数及其说明，如下表所示。 

StandardScaler类

参数名称	说明
with_mean	接收bool。若为True，表示在缩放数据前进行中心化，当数据为稀疏矩阵时，将不起作用并可能引起异常。默认为True
with_std	接收bool。表示是否将数据缩放为单位方差或单位标准差。默认为True

StandardScaler对象拥有4个属性，如下表所示。

StandardScaler对象

属性	说明
scale_	每个特征对应的数据缩放比例
mean_	每个特征的均值
var_	每个特征的方差
n_samples_seen_	由估算器分配给每个特征的样本数

StandardScaler对象提供7种方法，如下表所示。

StandardScaler对象提供7种方法

方法	格式	说明
fit	fit(X, y=None)	计算标准化所需的均值与方差
fit_transform	fit_transform(X, y=None, **fit_params)	先应用fit方法，然后应用transform方法
get_params	get_params(deep=True)	获取对象参数
inverse_transform	inverse_transform(X, copy=None)	将应用了变换的数据转换回原数据
partial_fit	partial_fit(X, y=None)	在线fit方法
set_params	set_params(**params)	设置对象参数
transform	transform(X, y='deprecated', copy=None)	对数据X进行转换

数据预处理——标准差标准化 

标准差标准化

样本	收入	年龄
1	7688	32
2	5788	29
3	4600	25
4	8900	35
5	9600	38
6	8100	33

from sklearn import preprocessing
import numpy as np
x_a = np.array([[7688,32],[5788,29],
                [4600,25],[8900,35]])
x_b = np.array([[9600,38],[8100,33]])

std_transformer = preprocessing.StandardScaler().fit(x_a)
x_train = preprocessing.StandardScaler().fit_transform(x_a)
x_test = preprocessing.StandardScaler().fit_transform(x_b)

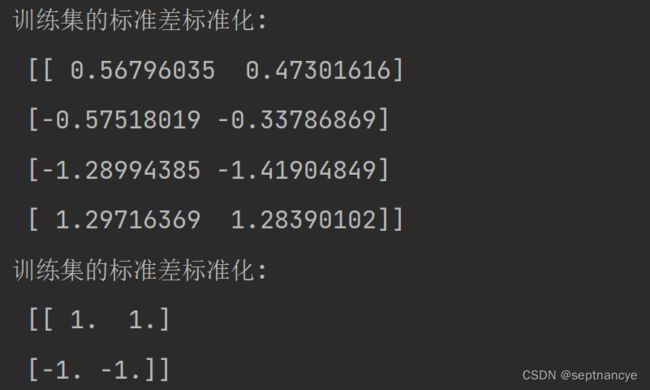
print('训练集的标准差标准化:\n' , x_train)
print('训练集的标准差标准化:\n' , x_test)

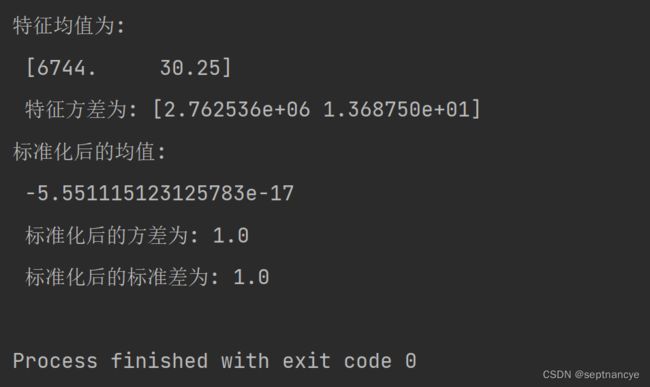
print('特征均值为: \n' , std_transformer.mean_,'\n' ,
      '特征方差为:', std_transformer.var_)

print('标准化后的均值: \n' , x_train.mean(),'\n' ,
      '标准化后的方差为:', x_test.var(),'\n',
      '标准化后的标准差为:',x_train.std())

 数据预处理——离差标准化

2.离差标准化

离差标准化是对原始数据的一种线性变换，是将原始数据的数值映射到[0,1]区间之间，转换公式如下式所示。

其中 max为样本数据的最大值， min为样本数据的最小值，max-min 为极差。离差标准化保留了原始数据值之间的联系，是消除量纲和数据取值范围影响最简单的方法。

preprocessing模块的MinMaxScaler类用于特征离差标准化处理。MinMaxScaler类能创建标离差标准化转换器，其基本语法格式如下。

class sklearn.preprocessing. MinMaxScaler (feature_range=(0, 1), copy=True)

 MinMaxScaler对象拥有5个属性，如下表所示。

MinMaxScaler对象的属性

属性	说明
min_	每个特征的最小调整
scale_	每个特征对应的数据缩放比例
data_min_	每个特征的最小值
data_max_	每个特征的最大值
data_range_	每个特征的范围

from sklearn import preprocessing
import numpy as np
x_a = np.array([[7688,32],[5788,29],
                [4600,25],[8900,35]])
x_b = np.array([[9600,38],[8100,33]])

mms_transformer = preprocessing.MinMaxScaler().fit(x_a)
print('生成规则后的离差标准化转换器为: \n',mms_transformer)
x_train = preprocessing.MinMaxScaler().fit_transform(x_a)
x_test = preprocessing.MinMaxScaler().fit_transform(x_b)
print('训练集的离差标准化: \n', x_train)
print('测试集的离差标准化: \n', x_test)
print('特征最大值为: \n',mms_transformer.data_max_,'\n',
      '特征最小值为：',mms_transformer.data_min_)
print('标准化后的均值: \n' , x_train.mean(),'\n' ,
      '标准化后的方差为:', x_test.var(),'\n',
      '标准化后的标准差为:',x_train.std())

数据预处理——非线性转换 

类似于标准化处理，将数据映射到[0,1]的均匀分布上。非线性转换将每个特征值转换到相同的范围内或者分布内，使异常数据变得平滑，可以消除不寻常的分布，并且比缩放方法更少受异常值的影响。但是，它会扭曲特征内和特征间的相关性和距离。

样本	收入	年龄
1	7688	32
2	5788	29
3	4600	25
4	8900	35
5	9600	38
6	8100	33

from sklearn import preprocessing
import numpy as np


x_a = np.array([[7688,32],[5788,29],
                [4600,25],[8900,35]])
x_b = np.array([[9600,38],[8100,33]])

quantile_transform = preprocessing.QuantileTransformer(n_quantiles=2,
                                                       random_state=0)
x_train = quantile_transform.fit_transform(x_a)
x_test = quantile_transform.fit_transform(x_b)

print('训练集的非线性转换: \n', x_train)
print('测试集的非线性转换: \n', x_test)

 数据预处理——归一化

归一化也称正则化，指依照特征矩阵的行处理数据，目的在于使样本向量在点乘运算或其他核函数计算相似性时拥有统一的标准，正则化规则为L2正则项时的转换公式如下所示。

其中 n 为 特征数， i 为 特征序号。

preprocessing模块的 Normalizer 类用于特征归一化化处理。 Normalizer 类用于创建归一化转换器，其基本语法格式如下。

class sklearn.preprocessing.Normalizer(norm='l2', copy=True)

Normalizer对象未提供属性，比 StandardScaler 对象少了 inverse_transform 和 partial_fit 方法， 如 下 表所 示 。

方法	格式	说明
fit	fit(X, y=None)	不进行任何操作，并使估计器保持不变，仅用于实现通常的API
fit_transform	fit_transform(X, y=None, **fit_params)	先应用fit方法，然后应用transform方法
get_params	get_params(deep=True)	获取对象参数
set_params	set_params(**params)	设置对象参数
transform	transform(X, y='deprecated', copy=None)	对数据X进行转换

from sklearn import preprocessing
import numpy as np


x_a = np.array([[7688,32],[5788,29],
                [4600,25],[8900,35]])
x_b = np.array([[9600,38],[8100,33]])

norm_transformer = preprocessing.Normalizer().fit(x_a)

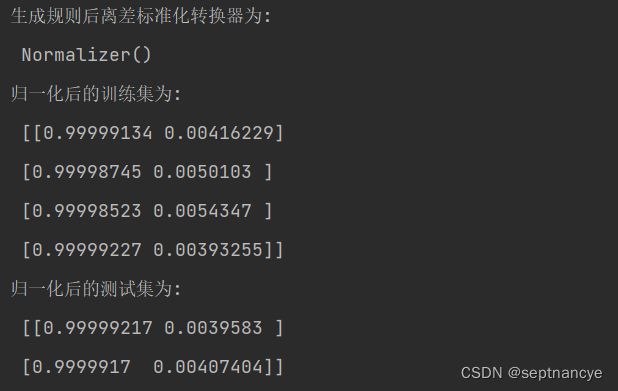
print('生成规则后离差标准化转换器为: \n', norm_transformer)
print('归一化后的训练集为: \n', norm_transformer.transform(x_a))
print('归一化后的测试集为: \n', norm_transformer.transform(x_b))

数据预处理——二值化

特征二值化指通过设置阈值，将特征值转换为0或1，当特征值大于阈值时转换为1，小于或等于阈值时转换为0。特征二值化与数据离散化不同，特征二值化后的值落在0或1，而数据离散化落在所属区间。

preprocessing模块的Binarizer类用于特征二值化。Binarizer类用于创建二值化转换器，其基本语法格式如下 

class sklearn.preprocessing.Binarizer(threshold=0.0, copy=True)

 Binarizer对象较StandardScaler少了partial_fit和inverse_transform方法，如下表所示。

方法	格式	说明
fit	fit(X, y=None)	不进行任何操作，并使估计器保持不变，仅用于实现通常的API
fit_transform	fit_transform(X, y=None, **fit_params)	先应用fit方法，然后应用transform方法
get_params	get_params(deep=True)	获取对象参数
set_params	set_params(**params)	设置对象参数
transform	transform(X, y='deprecated', copy=None)	对数据X进行转换

from sklearn import preprocessing
import numpy as np


x_a = np.array([[7688,32],[5788,29],
                [4600,25],[8900,35]])
x_b = np.array([[9600,38],[8100,33]])

bin_transformer = preprocessing.Binarizer(threshold=100).fit(x_a)
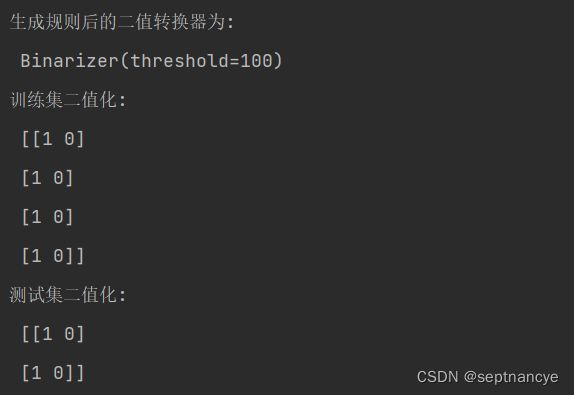
print('生成规则后的二值转换器为: \n',bin_transformer)

x_train = preprocessing.Binarizer(threshold=100).fit_transform(x_a)
x_test = preprocessing.Binarizer(threshold=100).fit_transform(x_b)
print('训练集二值化: \n', x_train)
print('测试集二值化: \n',x_test)

 数据预处理——独热编码

from sklearn import preprocessing
import numpy as np

x_train = np.array([['男', '北京', '已婚'],
                    ['男', '上海', '未婚'],
                    ['女', '广州', '已婚']])
x_test = np.array([['男', '北京', '未婚']])


def auto_coder(X):
    for i in range(X.shape[1]):
        X[:, i] = preprocessing.LabelEncoder().fit_transform(X[:, i])
    X = X.astype(int)
    return X

x_train_num = auto_coder(x_train)
print('转换为数值型后的训练集为: \n', x_train_num)

oe_transformer = preprocessing.OneHotEncoder().fit(x_train_num)
print('生成规则后的独热编码转换器为: \n', oe_transformer)

print('独热编码后的训练集为: \n',
      oe_transformer.transform(x_train_num).toarray())

x_test_num = auto_coder(x_test)
print('独热编码后的测试集为: \n',
      oe_transformer.transform(x_test_num).toarray())

 数据预处理——缺失值的插补

import numpy as np
from sklearn.impute import SimpleImputer

imp = SimpleImputer(missing_values = np.nan, strategy = 'mean')
X = np.array([[0,4],[np.NaN,5],[np.NaN,0],[3,7]])

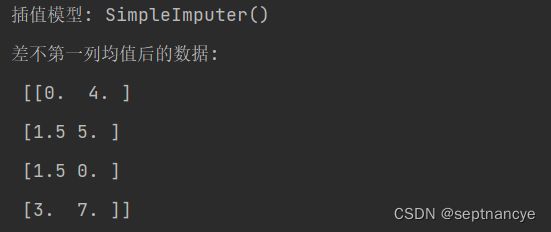
print('插值模型:', imp.fit(X))
print('差不第一列均值后的数据: \n', imp.transform(X))

 数据预处理——生成多项式特征

import numpy as np
from sklearn.preprocessing import PolynomialFeatures

poly = PolynomialFeatures(2)
X = np.array([[0,4],[1,5],[2,6],[3,7]])

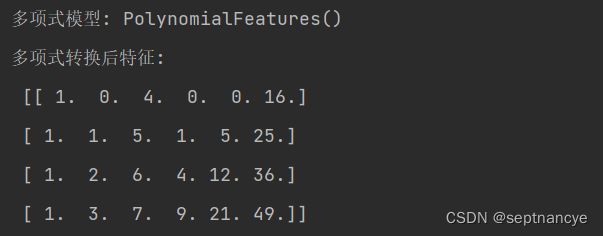
print('多项式模型:', poly.fit(X))
print('多项式转换后特征: \n', poly.transform(X))

 2,降维

PCA

from sklearn import datasets

iris = datasets.load_iris()
x = iris.data

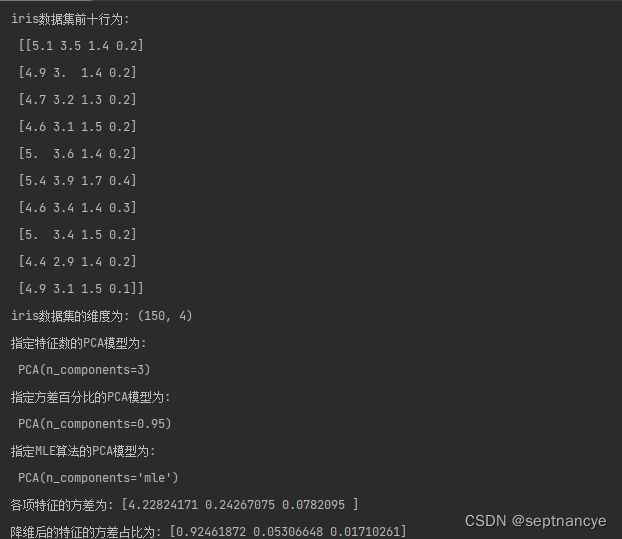
print('iris数据集前十行为: \n', x[: 10])
print('iris数据集的维度为:', x.shape)

from sklearn.decomposition import PCA

pca = PCA(n_components= 3).fit(x)
print('指定特征数的PCA模型为: \n', pca)
pcal = PCA(n_components= 0.95).fit(x)
print('指定方差百分比的PCA模型为: \n', pcal)
pca2 = PCA(n_components= 'mle').fit(x)
print("指定MLE算法的PCA模型为: \n", pca2)

print('各项特征的方差为:', pca.explained_variance_)
print('降维后的特征的方差占比为:',pca.explained_variance_ratio_)

x_pca = pca.transform(x)
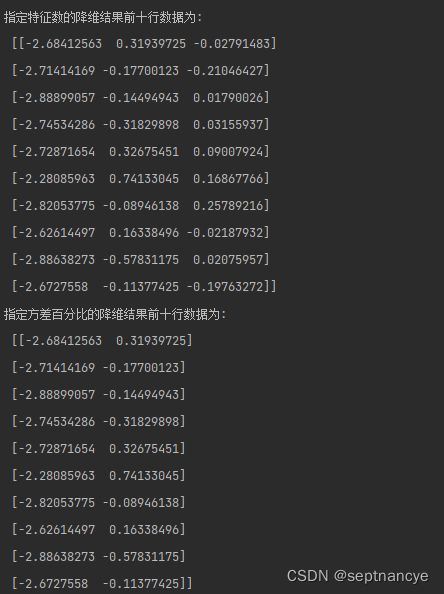
print('指定特征数的降维结果前十行数据为: \n', x_pca[: 10])

x_pcal = pcal.transform(x)
print('指定方差百分比的降维结果前十行数据为: \n', x_pcal[: 10])

x_pca2 = pca2.transform(x)
print('MLE算法的降维结果前十行数据为: \n', x_pca2[: 10])

 ICA

import numpy as np
from scipy import signal

np.random.seed(0)
n_samples = 2000
time = np.linspace(0,8,n_samples)

waft1 = np.sin(2*time)
waft2 = np.sign(3*time)
waft3 = signal.sawtooth(2*np.pi*time)
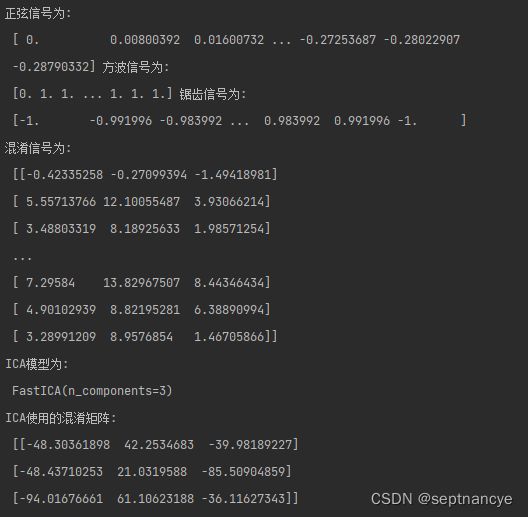
print('正弦信号为: \n', waft1,
      '方波信号为: \n', waft2,
       '锯齿信号为: \n', waft3)

waft = np.c_[waft1,waft2,waft3]
waft += 0.2*np.random.normal(size= waft.shape)
waft /= waft.std(axis = 0)
arr = np.array([[1,1,1],[0.5,2,1.0],[1.5,1.0,2.0]])
mix_waft = np.dot(waft,arr.T)
print('混淆信号为: \n', mix_waft)

from sklearn.decomposition import FastICA
ica = FastICA(n_components= 3).fit(mix_waft)
print('ICA模型为: \n', ica)

ica_mixing = ica.mixing_
print('ICA使用的混淆矩阵: \n', ica_mixing)

import matplotlib.pyplot as plt

waft_ica = ica.transform(mix_waft)
waft_pca = PCA(n_components= 3).fit(mix_waft)
plt.figure(figsize= [12,6])
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False
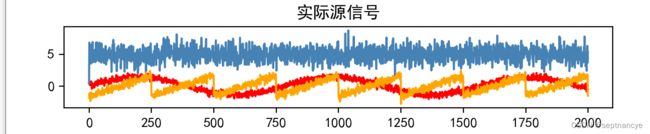
models = [mix_waft, waft, waft_ica, waft_pca]
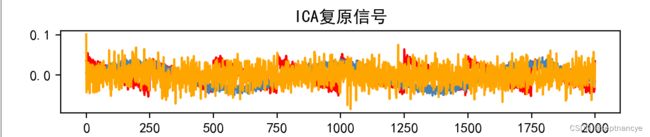
names = ['混淆信号','实际源信号','ICA复原信号','PCA复原信号']
colors = ['red','steelblue','orange']

for i, (model, name) in enumerate(zip(models,names), 1):
    plt.subplot(4,1,i)
    plt.title(name)
    for sig, color in zip(model.T,colors):
        plt.plot(sig, color = color)
    plt.subplots_adjust(0.09,0.04,0.94,0.94,0.26,0.46)
    plt.show()

 LDA

from sklearn import datasets

iris = datasets.load_iris()
x = iris.data

print('iris数据集前十行为: \n', x[: 10])
print('iris数据集的维度为:', x.shape)

from sklearn.decomposition import PCA

pca = PCA(n_components= 3).fit(x)
print('指定特征数的PCA模型为: \n', pca)
pcal = PCA(n_components= 0.95).fit(x)
print('指定方差百分比的PCA模型为: \n', pcal)
pca2 = PCA(n_components= 'mle').fit(x)
print("指定MLE算法的PCA模型为: \n", pca2)

print('各项特征的方差为:', pca.explained_variance_)
print('降维后的特征的方差占比为:',pca.explained_variance_ratio_)

x_pca = pca.transform(x)
print('指定特征数的降维结果前十行数据为: \n', x_pca[: 10])

x_pcal = pcal.transform(x)
print('指定方差百分比的降维结果前十行数据为: \n', x_pcal[: 10])

x_pca2 = pca2.transform(x)
print('MLE算法的降维结果前十行数据为: \n', x_pca2[: 10])

import numpy as np
from scipy import signal

np.random.seed(0)
n_samples = 2000
time = np.linspace(0,8,n_samples)

waft1 = np.sin(2*time)
waft2 = np.sign(3*time)
waft3 = signal.sawtooth(2*np.pi*time)
print('正弦信号为: \n', waft1,
      '方波信号为: \n', waft2,
       '锯齿信号为: \n', waft3)

waft = np.c_[waft1,waft2,waft3]
waft += 0.2*np.random.normal(size= waft.shape)
waft /= waft.std(axis = 0)
arr = np.array([[1,1,1],[0.5,2,1.0],[1.5,1.0,2.0]])
mix_waft = np.dot(waft,arr.T)
print('混淆信号为: \n', mix_waft)

from sklearn.decomposition import FastICA
ica = FastICA(n_components= 3).fit(mix_waft)
print('ICA模型为: \n', ica)

ica_mixing = ica.mixing_
print('ICA使用的混淆矩阵: \n', ica_mixing)

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

y = iris.target
lda = LinearDiscriminantAnalysis(n_components= 2).fit(x, y)
print('LDA模型为: \n', lda)

pca = PCA(n_components= 2).fit(x)
print('PCA模型为: \n', pca)

print('LDA模型方差百分比为:', lda.explained_variance_ratio_)
print('LDA模型类标签为:', lda.classes_)

target_name = iris.target_names
x_lda = lda.transform(x)
x_pca = pca.transform(x)

plt.figure()
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False
colors = ['navy','turquoise','darkorange']
markers = ['*','.','d']
lw = 2
for color,i,target_name,marker in zip(colors,[0,1,2],
                                      target_name,markers):
    plt.scatter(x_lda[y ==i,0],x_lda[y ==i,1],
                alpha=.8, color=color,label=target_name,
                marker=marker)
plt.legend(loc = 'best',shadow = False, scatterpoints = 1)
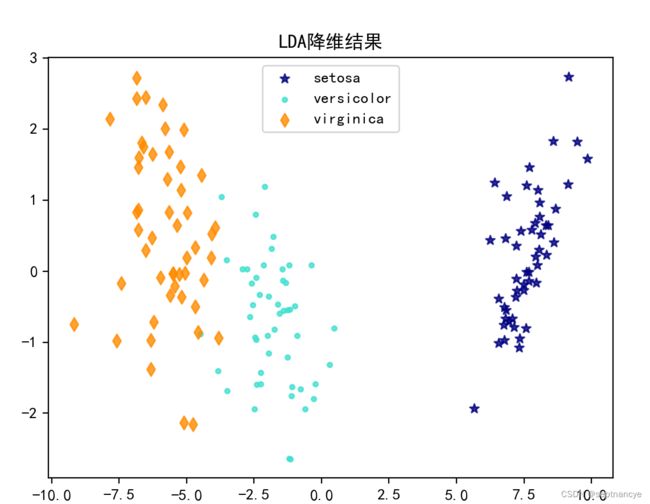
plt.title('LDA降维结果')
plt.show()