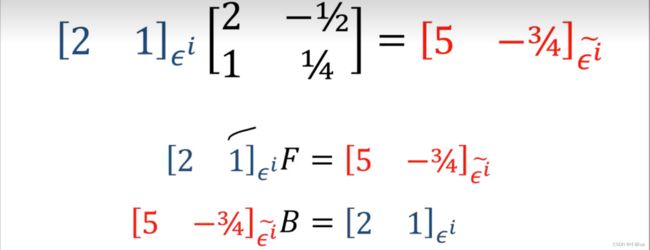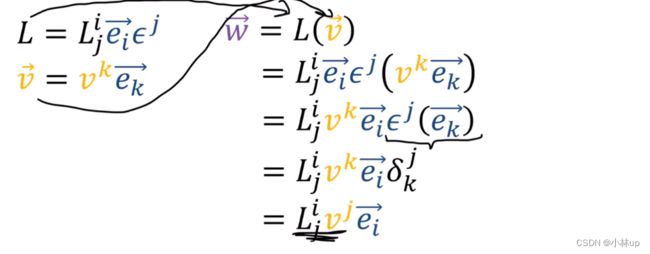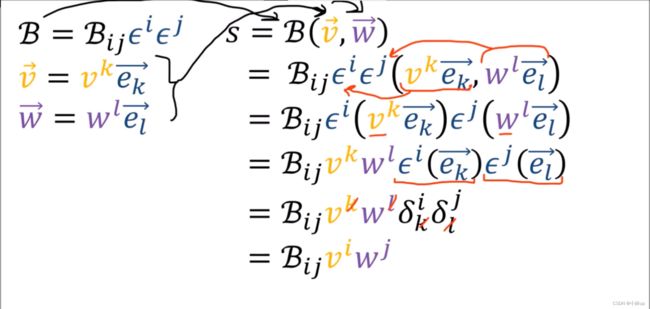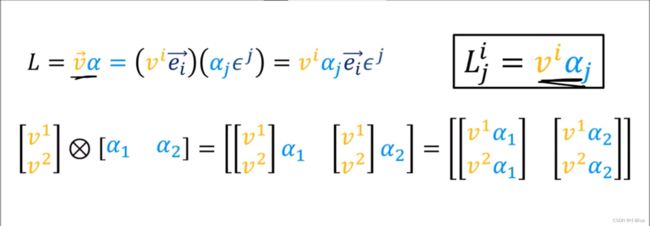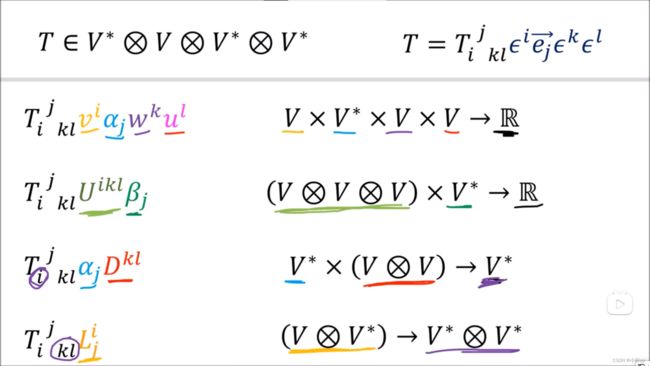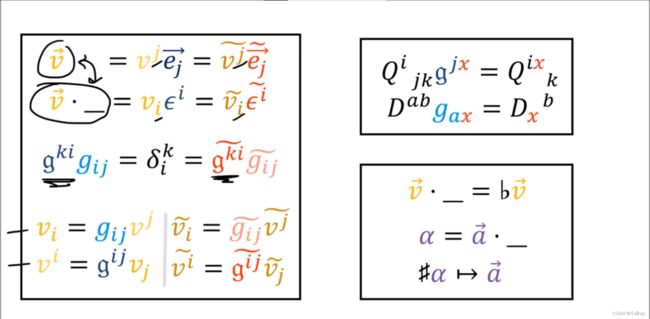张量分析入门笔记 (Tensor For Beginner)
前言
学习的时候感觉要学一下张量，在B站看了一个视频，记录一下，参考的是B站视频【机翻】张量分析入门 (Tensor For Beginner)
- 前言
- 1. 张量的定义 Tenson Definition
- 2. 张量的前向和后向的转换 Forward and Backward Transformation
- 3. 向量 Vector
- 4. 余向量 Covector
- 5. 线性映射 Linear Map
- 6. 度规张量 The Metric Tensor
- 7. 张量积 Tensor Product
- 8. 张量积空间 Tensor Product Space
- 9. 张量指标的上升和下降 Raising or Lowing Indexes
1. 张量的定义 Tenson Definition
引入：一只铅笔，我们让它朝着门的方向，铅笔的朝向是始终不变的（这是本质的东西），但是铅笔在不同坐标系下的坐标却不一样（哦，可能需要进行坐标变换）。
张量是不变的，但是它的坐标在不同的坐标系下是不同的（张量的坐标定义）。
张量：向量和共变向量的组合使用张量积进行定义。
一个很直观的抽象张量的方法是从微积分的求偏导和梯度得到——雅克比矩阵。
2. 张量的前向和后向的转换 Forward and Backward Transformation
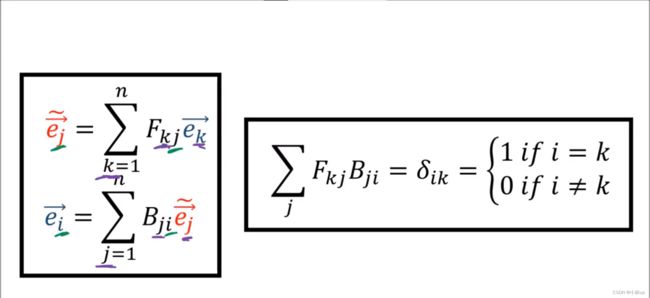
有点类似机器人学的坐标转换，旧坐标系和新坐标系的互相转换。
前向的转换（旧坐标系转换到新坐标系）
后向的转换（新坐标系转换到旧坐标系）
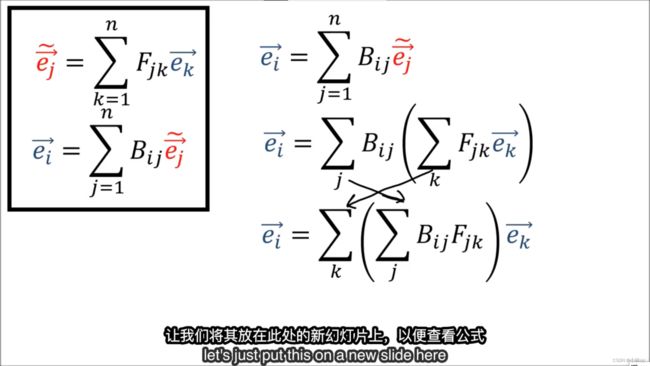
我们可以容易验证上面的正向和反向的转换矩阵互为逆矩阵。即 B F = I BF=I BF=I
高维的情况：
于是在高维的情况下我们也可以证明 B F BF BF相乘的矩阵是单位阵。
【上面图片 F j k F_{jk} Fjk为 F k j F_{kj} Fkj， B i j B_{ij} Bij为 B j i B_{ji} Bji，作者说ppt写错了】
总结：最后就可以引出Kronecker Delta记号 δ i k \delta_{ik} δik。
3. 向量 Vector
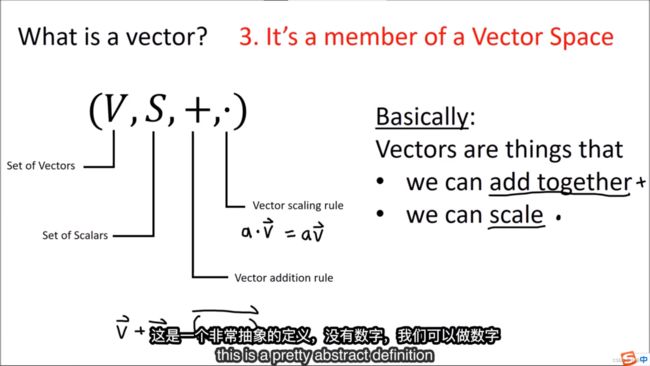
引入了向量空间，需要定义一个集合，并且定义向量内部的元素类型（比如是一个实数），向量的运算性质（数乘和加法）。
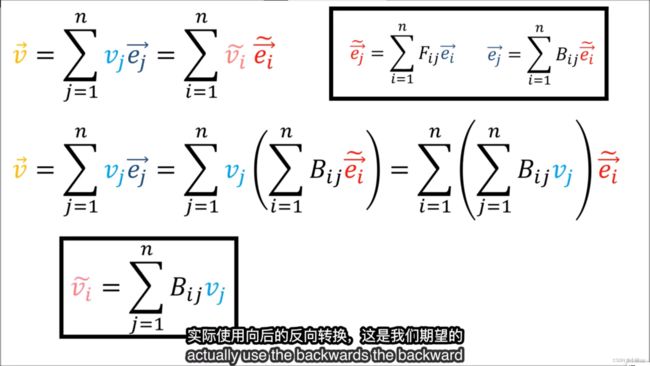
向量的正反变换为B和F，坐标的对应正反变换为F和B。
两个例子：
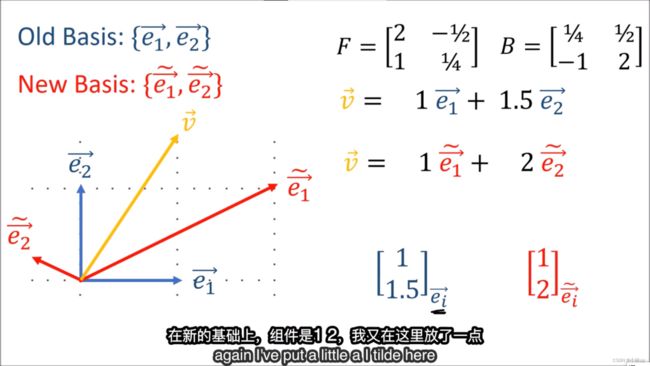
- 例子1：不同基向量下的坐标（只使用数乘）
基向量长度增加了，坐标的值减少了。
- 例子2：不同基向量下的坐标（基向量旋转）
基向量长度不变进行顺时针旋转，相对的向量坐标的变化是相对原来的坐标系逆时针旋转，更接近 e 2 ⃗ \vec{e_2} e2，变化方向也是相反的。
基向量和向量分量的变换公式：
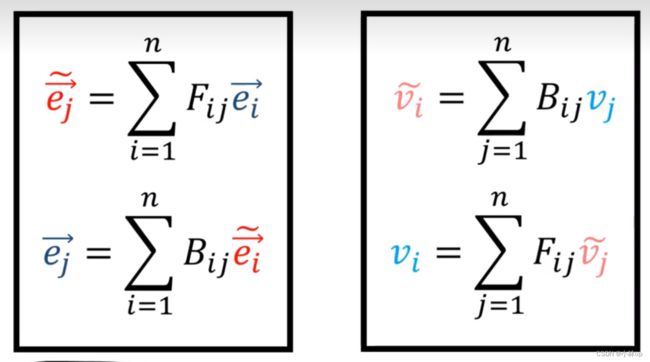
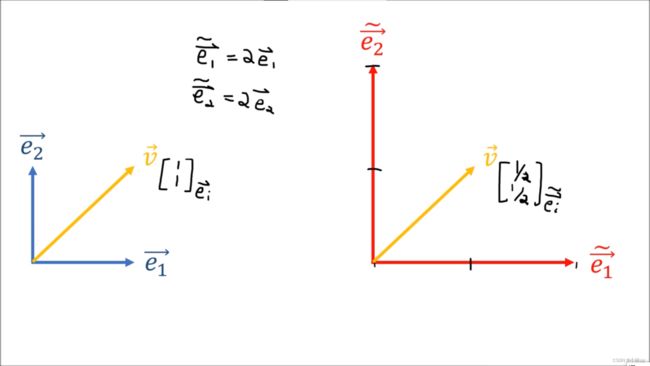
这个时候基向量分量和向量是相反的关系，我们称他是contravariant 的。
为了区分这种相反的关系，我们需要把放在向量分量的下标改为上标，提示我们它是逆变张量（当基向量变大时，对应的向量分量变小）。
4. 余向量 Covector
我们可以基本认为余向量是一个行向量。它相当于一个函数（矢量的点积）将列向量转化为一个实数：
验证加法：
验证数乘：
这个函数相当于是一个线性函数。
我们可以将这个过程进行一个可视化。
作用以后相当于求向量落在那条线上（有点类似于等高线）。
余向量有很好的数乘和加法的性质。它所在的空间可以看做是向量空间的一个对偶空间。（加法和数乘的定义不一样）
最后做一个总结：
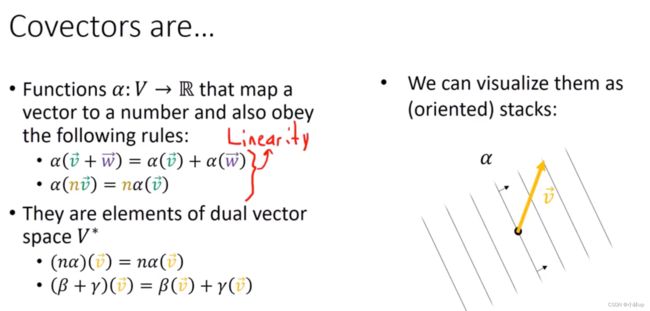
我们可以理解为Covector协变张量就是行向量，而其向量分量是这个协变张量作用在列向量（点积）。
注意
- 协变张量相当于一个函数关系： α : V ↦ R \alpha:V \mapsto\R α:V↦R
- 协变张量不存在于向量空间 V V V中
- 我们不能像向量一样使用基向量 { e 1 ⃗ , e 2 ⃗ } \{\vec{e_1},\vec{e_2}\} {e1,e2}对协变张量进行测量。
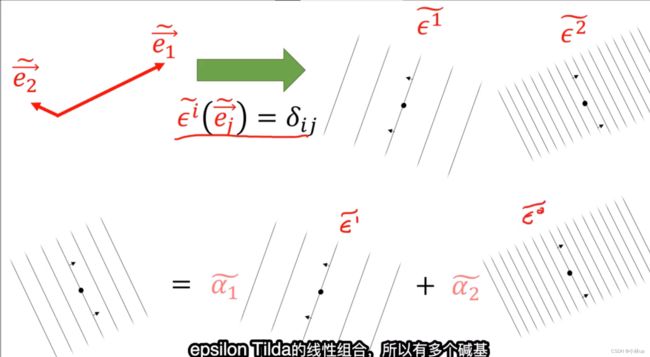
我们引入一个记号 ϵ \epsilon ϵ作为对偶基，并按上图进行定义，这样又可以引入Kronecker Delta记号 δ i k \delta_{ik} δik。
ϵ \epsilon ϵ的作用是将向量投影到协变张量的方向。
协变张量 α \alpha α相当于定义了一个对偶基。几何直观是：
这里又引入Kronecker Delta记号 δ i k \delta_{ik} δik。
协变张量可以有不同的表达方式
协变张量可以看到坐标分量：
2 × 2 + 1 × 1 = 5 2\times 2+1\times 1=5 2×2+1×1=5
坐标（旧坐标换到新坐标）：
2 e 1 + 1 e 2 = e ~ 1 2\mathbf{e}_1+1\mathbf{e}_2={\mathbf{\tilde{e}}}_1 2e1+1e2=e~1
都是同样的变大，不存在逆变张量。
这和前面讲的逆变张量有很大的区别：旧坐标分量到新坐标分量在逆变张量用的是 B B B进行变换，反之用 F F F；旧坐标分量到新坐标分量在协变张量用的是 F F F进行变换，反之用 B B B。
我们可以看看协变张量的计算规则：
ϵ \epsilon ϵ是对偶基，而 e e e是原始基。我们可以看到旧对偶基 ϵ \epsilon ϵ到新对偶基 ϵ ~ \tilde{\epsilon} ϵ~的系数矩阵和原始基 e ~ \tilde{e} e~到新基 e e e的系数矩阵差一个转置。
对于高维的情况，我们有：
因为 Q F = I QF=I QF=I， B F = I BF=I BF=I，所以 Q = B Q=B Q=B。这就是说从旧的对偶基变换到新的对偶基需要使用 B B B（反向传递进行变换）。于是我们就知道 ϵ \epsilon ϵ需要使用上标，因为它和基向量 e e e的变换方向是相反的。
这是基向量和对偶向量之间的变换关系，它们的变换规则是完全相反的。
基向量变大，对应的向量分量也会变大。
下面这张图总结了前面所讲的协变和逆变变换。
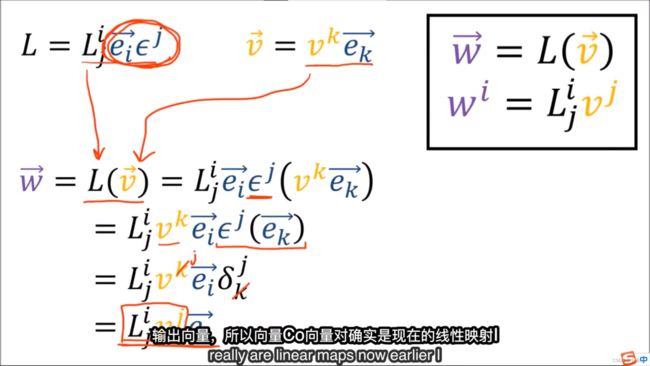
5. 线性映射 Linear Map
线性映射转换输入的向量，但是不会转换基。几何直观上进行了这样的转换：
尽管输入和输出的向量可能是不一样的，但是它们都是在同一组基下进行表示的。
在线性变换的作用下，网格线仍然是平行的，均匀分布的，而且原点是不变的。但是平移不是线性变换，因为原点的位置发生了改变。
线性映射需要满足以上三点。其中后两点被称为是线性性。
加法的几何直观：
数乘的几何直观：
以上两张图片通过代数运算给出了线性映射（矩阵）的计算规则。
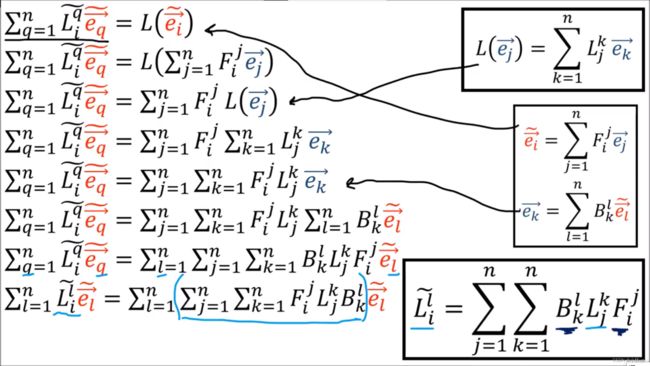
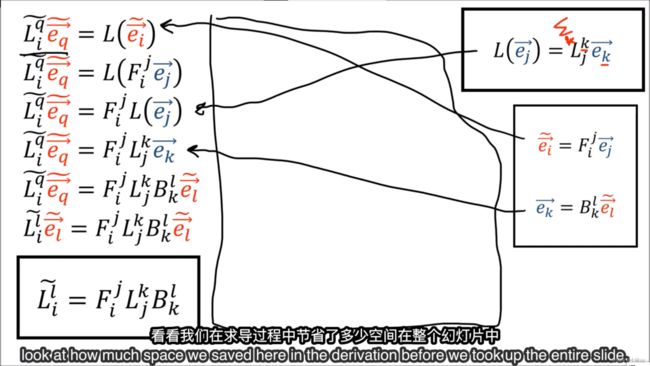
探究：在不同基下的坐标进行线性变换
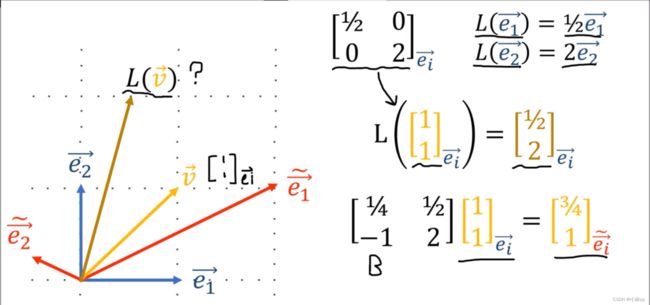
我们不能再使用原来的基下的变换矩阵，我们需要求新的基下的变换矩阵。
于是我们的问题就可以解决了。
然后就引入了爱因斯坦求和法则：
矩阵乘一个单位阵还是自己用张量表示：
我们还可以得到线性变换反向转换的表达式：
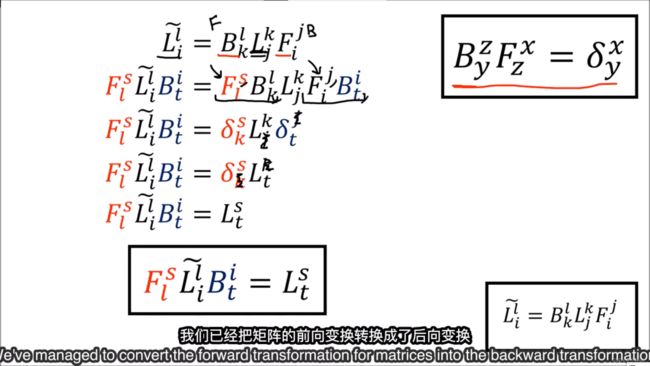
那么现在我们就学了：
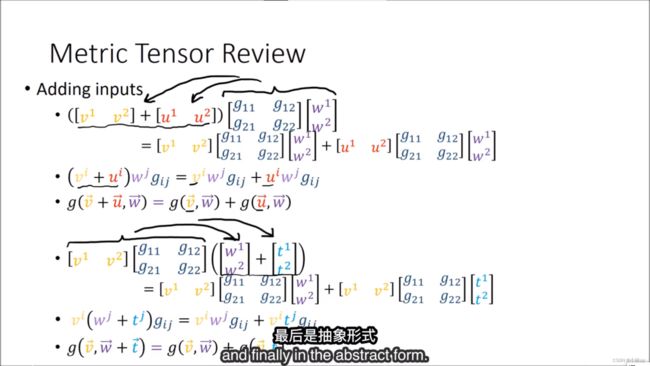
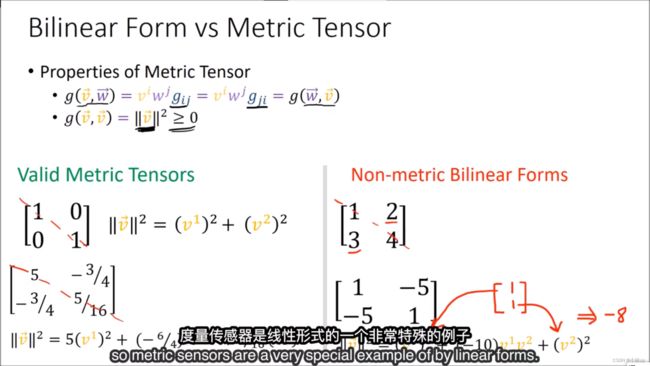
6. 度规张量 The Metric Tensor
于是这样就引出了度规张量（线性代数的二次型派上了用场）
举个例子：
于是长度我们可以计算，角度我们也可以计算。
目前学到的张量。
对于度规张量的数乘。
对于度规张量的加法。
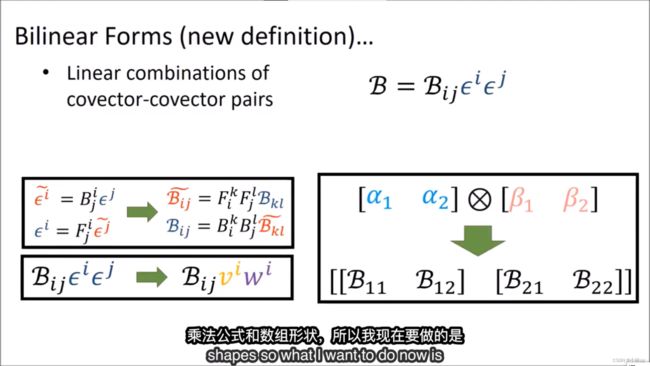
于是（0-2）型张量引出了二次型。
二次型有双线性，可以类比与余向量。
这里的双线性指的是一个输入线性变化时，另一个输入保持不变。
对于（0-2）型tensor还有以上的两个性质。
不是所有的度规形式都是张量，需要满足上一张图的两个性质。
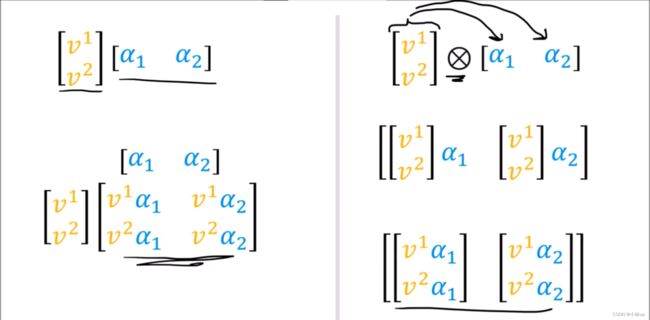
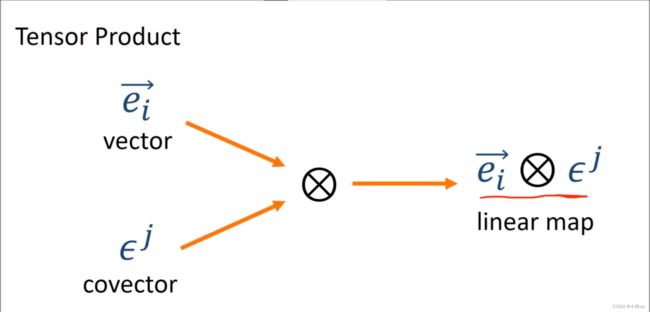
7. 张量积 Tensor Product
先复习一下我们之前学到的张量：
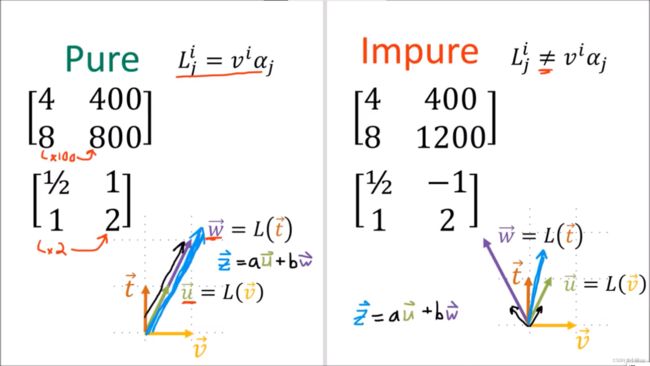
一个矩阵（线性映射）如果可以分解为一个列向量（向量）和一个行向量（余向量）相乘，称它是pure的。否则是impure的。
使用标准基和对偶基我们可以构造四个基本矩阵。
所有的 2 × 2 2\times 2 2×2的矩阵都可以写作是这四个基本矩阵的线性组合。我们称这四个矩阵是KaTeX parse error: Undefined control sequence: \time at position 2: 2\̲t̲i̲m̲e̲ ̲2型矩阵（线性映射）的基。
对于线性映射我们可以重新书写一下。如上所示，得到线性映射后的元素的计算的方式。
当然线性映射也可以选择其他的基。
我们可以对pure Linear Map和Impure Linear Map重新总结一下。接下来我们就可以引入张量的记号了。
为了简化对于张量积的符号还是写作左边的这种形式。
张量积给我们看线性映射带来了新的视角。
张量积（上图右边的一个直观的表达）。
对于二次型的形式我们也可以看成是两个余向量的形式，为什么呢？余向量需要有一个向量作为输入，这点和二次型需要两个向量输入很相似。
张量积给我们看二次型带来了新的视角。
好像使用张量积表示二次型不太对？
看上面的图我们呢知道只是形式不同罢了。
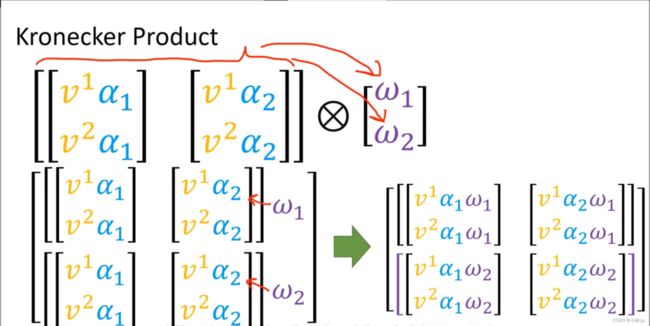
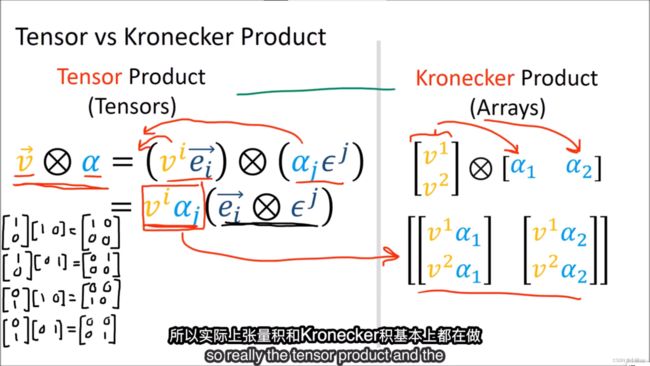
关于 ⊗ \otimes ⊗记号，分别可以作用于张量(张量积)和数组（Kronecker积）。
回顾一下标准基和对偶基。
张量积作用两个张量出来还是张量。
使用张量积我们也可以看到线性映射是怎么作用在向量上的。
上面两个图是使用Kronecker积作用在向量上。
其实两者在做类似的同样的事情，不过张量积将抽象的基也考虑进去了。
如前所述：使用张量积可以很简单地定义线性映射：
以及二次型。
接下来我们来看一些没见过的张量。
上面的图左边是(2-0)型张量，右边是(1-2)型张量。我们不禁要问：对于新的张量类型我们怎么定义坐标转换的规则？如果要计算 Q ( D ) Q(D) Q(D)，乘法公式是什么？以及矩阵的形状是什么样的？
上图解决了第一个问题：新的张量怎么进行不同的坐标转换？
上图解决了第二个问题：如果要计算 Q ( D ) Q(D) Q(D)，乘法公式是什么？答案是不唯一的，你有各种各样的组合方式。这样写写不清楚，我们还是需要按照爱因斯坦的求和法写出分量的表达式。
对于张量 D D D和张量 Q Q Q的表达形式如上图所示。其中 Q Q Q是一个三阶张量，可以有上面最后一图的表达方式。
矩阵的乘法在低维的张量很有用，但是在高维的情况下如前所述我们有很多种表达的形式，这是后再使用矩阵的乘法就不是特别好了。我们还是用爱因斯坦乘法来表示我们想要的张量乘法，不然容易发生混淆。
在很多情况下，我们只关注张量的分量。
现在我们再次回顾张量的乘定义，应该就很清楚了。
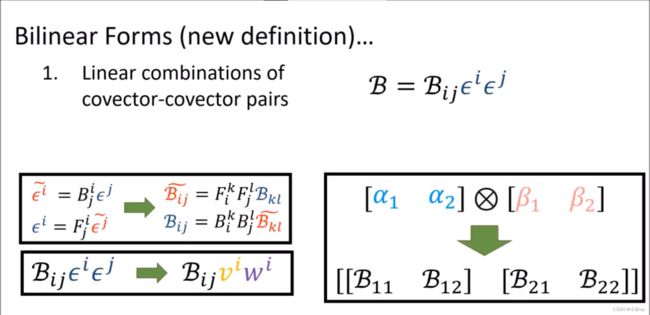
8. 张量积空间 Tensor Product Space
回顾：前面线性映射和二次型的例子
数乘（张量积和Kronecker积是类似的）
加法（张量积和Kronecker积是类似的）
总结一下我们有：
这在计算中很有用（参见上面两图）。
张量积定义的张量积空间（上图的最后一行）
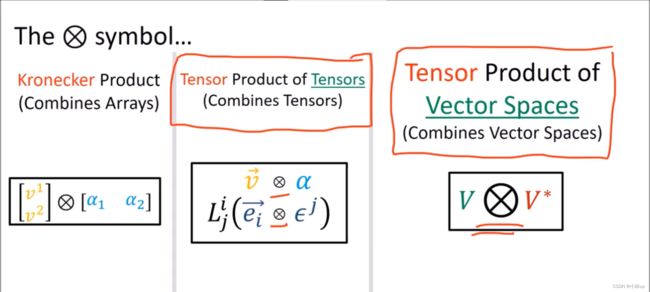
V ⊗ V ∗ V\otimes V^* V⊗V∗的元素是什么？
上图说明： V ⊗ V ∗ V\otimes V^* V⊗V∗的元素是（1,1）型的张量。
我们要记得向量分量用的是上标，而余向量分量使用的是下标。
将线性映射进行不同的作用我们可以映射到不同的空间。
另一个例子是二次型。
将二次型进行不同的作用我们可以映射到不同的空间。
使用不同的张量空间进行张量积我们得到不同的张量积空间。
在张量的计算中我们可以使用数乘和加法来进行计算：
这就引出了高维张量的多线性映射（一个量发生改变，但是其他的量不变，仍然保持线性性）：
总结：
9. 张量指标的上升和下降 Raising or Lowing Indexes
现在我们有两个空间，我们怎么建立两个空间的关系呢？
很自然地我们可以想到将它们对应的基进行匹配：
但是这种方法并不好。因为两个坐标转换的规则不一样一个是乘以矩阵 F F F，一个是乘以矩阵 B B B。
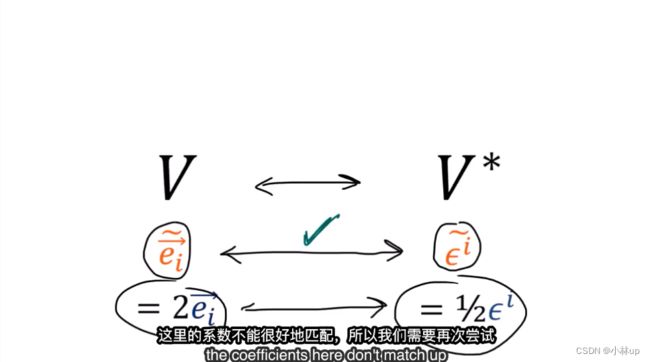
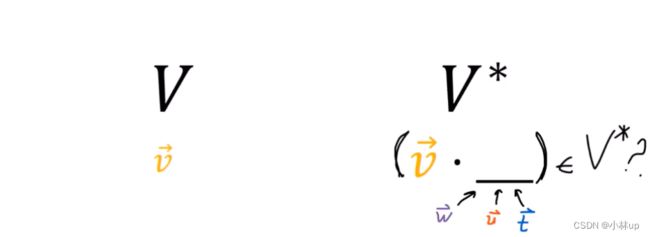
上面的图片表明( v ⃗ ⋅ \vec{v}\cdot v⋅_)确实属于 V ∗ V^* V∗。
不依赖于基我们就找到了两者很好的匹配关系。
类比度规张量我们可以得到( v ⃗ ⋅ \vec{v}\cdot v⋅_)的表达式。
总结：
注意这两个不一样除非 g i j = δ i j g_{ij}=\delta_{ij} gij=δij：
利用 g g g可以定义空间 V V V到空间 V ∗ V^* V∗的映射，反过来怎么办呢？
g g g把上标变成下标。 g \mathfrak{g} g把下标变成上标。
这样我们可以把张量空间进行各种不同的映射。
指标从上标变成下标也可以使用符号 b b b，从下标变成上标也可以使用符号 # \# #，类似于钢琴里的升调和降调。
参考：
【机翻】张量分析入门 (Tensor For Beginner)