详解机器人标定
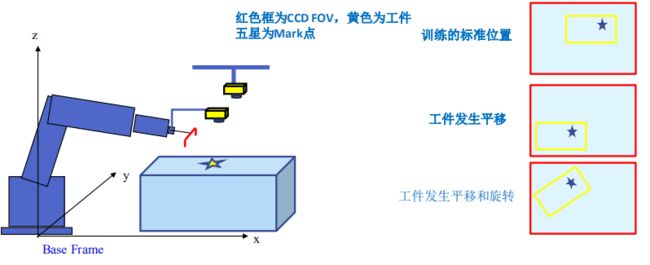
相机固定不动, 上往下看引导机器人移动
机器人与视觉标定理论详解
相机固定不动, 上往下看引导机器人移动
1.相机非线性校正
使用标定板做非线性校正
2.相机与机器人做9点标定
可以使用机器人扎9个点,或者机器人抓住工件摆放9个位置,得到9个机械坐标,相机也得到9个像素坐标,然后标定
3.计算机器人的旋转中心
机器人抓取工件分别旋转三个角度摆放到相机视野内,相机可以得到三个坐标值,通过三个坐标值拟合圆获得圆心坐标即为旋转中心
4.相机通过公式计算得出最终的输出结果
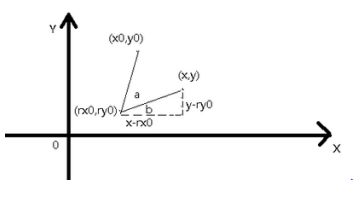
(rx0, ry0)为旋转中心,( x, y)为被旋转的点,(x0,y0)旋转后的点
x0= cos (a) * (x-rx0) – sin (a) * (y-ry0) +rx0
y0= cos (a) * (y-ry0) + sin (a) * (x-rx0) +ry0
相机固定不动, 下往上看
1.相机非线性校正
使用机器人吸起标定板做非线性校正
2.相机与机器人做9点标定
可以使用实物标定,机器人抓住工件摆放9个位置,得到9个机械坐标,相机也得到9个像素坐标,然后标定。
参考上面的上往下看。
相机固定在机器人上,离旋转中心较近
1、相机非线性矫正
2、相机与机器人做9点标定
可以使用实物标定,机器人抓住工件摆放9个位置,得到9个机械坐标,相机也得到9个像素坐标,(机器人每次需要回到固定位置拍照),然后标定
3、计算机器人的旋转中心
机器人抓取工件分别旋转三个角度摆放到相机视野内,相机可以得到三个坐标值,通过三个坐标值拟合圆获得圆心坐标即为旋转中心
4、相机通过公式计算得出最终输出结果
相机固定在机器人上,离旋转中心很远
1、相机非线性矫正
2、相机与机器人做9点标定
3、计算机器人的旋转中心
4、相机通过公式计算得出最终输出结果
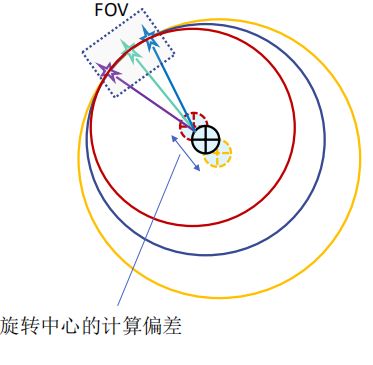
注:由于选择中心距离视野很远,通常拟合出来的旋转中心存在比较大的误差,给定位精度造成影响。
分离轴
分离轴的设计方式有很多,XY + θ, X+Y θ, X θ+Y….,具体状况具体分析,目的是要找到旋转中心,做好9点标定。
1.相机非线性校正
2.相机与机器人做9点标定
3.计算机器人的旋转中心
4.相机通过公式计算得出最终的输出结果
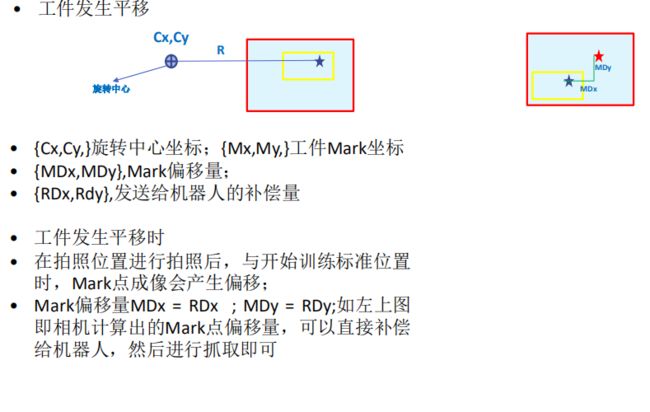
旋转中心标定说明
旋转中心方法用于所有机器人与视觉配合场景
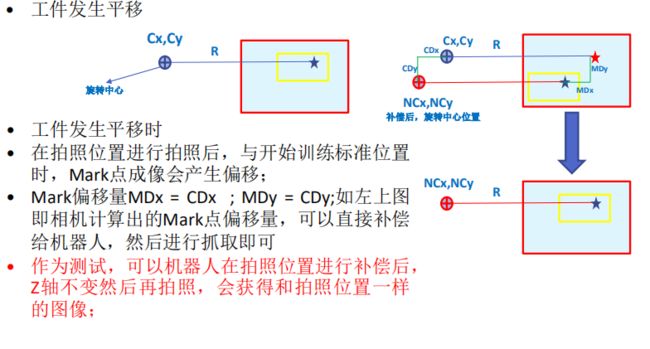
方法:计算工件实际发生的偏移量和旋转量,结合机器人的旋转中心进行二次补偿后,把补偿量
发送给机器人,然后机器人把补偿量补偿后进行抓取或放置即可;
点坐标旋转方法
计算某个点绕另外一点旋转一定角度后的坐标,如图:
机器人与视觉标定理论详解
A(x,y)绕B(rx0,ry0)旋转a度后的位置为C(x0,y0),则有如下关系式:
x0= cos (a) * (x-rx0) – sin (a) * (y-ry0) +rx0
y0= cos (a) * (y-ry0) + sin (a) * (x-rx0) +ry0
下面计算所有的旋转和偏移量均是基于上面的公式
旋转中心标定说明
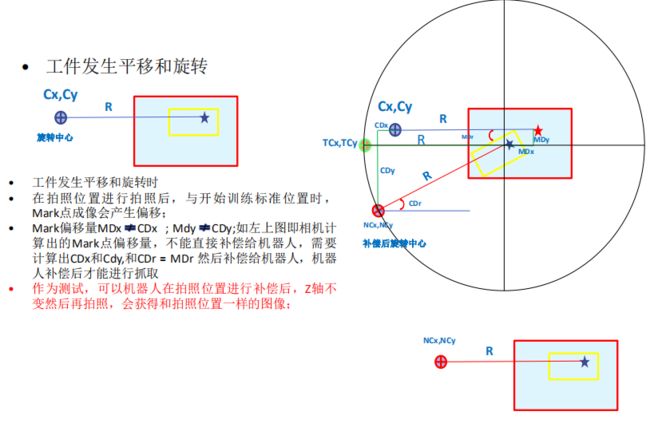
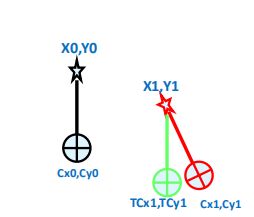
STD方法的计算:
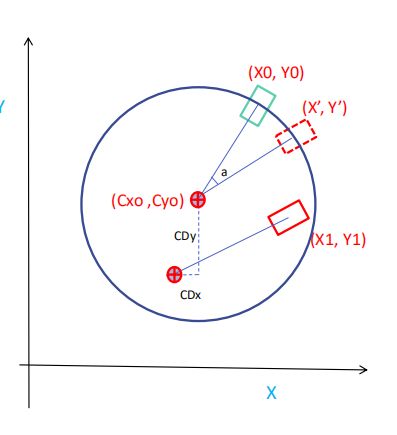
CDx= cos (a) * (Cx0-X0) – sin (a) * (Cy0-Y0) + X1 – Cx0
CDy= cos (a) * (Cy0-Y0) + sin (a) * (Cx0-X0) + Y1 – Cy0
X’= cos (a) * (X0-Cx0) – sin (a) * (Y0-Cy0) + Cx0
Y’= cos (a) * (Y0-Cy0) – sin (a) * (X0-Cx0) + Cy0
CDx=X1-X’
Cdy=Y1-Y’
这里是机器人在取料之前,先把自己的角度补正到与 物料当前角度一致,到(X’,Y’)位置处,然后移动 CDx,Cdy,与物料位置也重合,然后去取料。这样就保证了每次取料后,物料相对于机器人的位置 一致,因此直接往目标位置放就可以。这种方式由于是取物料的时候调整位置,因此适用于 相机固定在机械手上、相机固定安装从上往下看的方式。如果相机固定安装从下往上看,由于机器人这时候已经取完料了,就不适合使用了。
特别注意
这里计算到的Cdx和Cdy一定要补偿到机器人的取料位置里,不能补偿到 放料位置。旋转中心方法计算到的偏差可以直接补偿到放料位置。原因如下:
旋转中心法的计算:
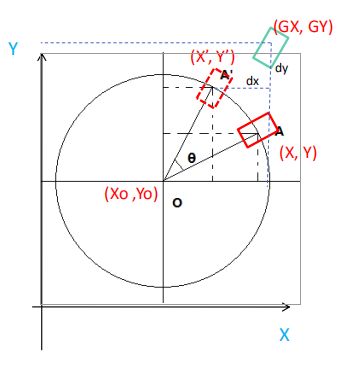
(X,Y)是定位到的产品位置,(GX,GY)是标准模板位置,(X’,Y’)是补偿了角度后的新位置,则:
X’ = cos θ * (X-Xo) – sin θ *(Y-Yo) + Xo;
Y’ = cos θ* (Y-Yo) + sin θ* (X-Xo) + Yo;
Offset X=X’-GX
Offset Y=Y’-GY
Offset Theta= θ
求旋转中心方法
当相机FOV与旋转中心很近,可以用旋转3点以上拟合一个圆求圆心
当相机FOV与旋转中心很远,使用旋转3或多个点求圆心,准确性会很差。
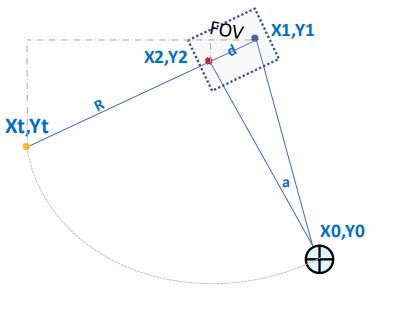
解法
(X0,Y0)为旋转中心, (X1,Y1)及(X2,Y2)为工件在视野中旋转角度a的前后坐标,(Xt,Yt)为两点连线的延长。
d = √(X2-X1)^2 + (Y2-Y1)^2
角度a
R = d/2/sin(a/2)
R/d = (Xt-X1)/(X2-X1)
R/d = (Yt-Y1)/(Y2-Y1)
Xt = (1-R/d)*X1 + (R/d)*X2
Yt = (1-R/d)*Y1 + (R/d)*Y2
X0= cos (90-a/2) * (Xt-X1) – sin (90-a/2) * (Yt-Y1) +X1
Y0= cos (90-a/2) * (Yt-Y1) + sin (90-a/2) * (Xt-X1) +Y1
角度:X+ Y+ 为正,反之为负
旋转中心标定—计算补偿
CDx Cdy计算过程,旋转角度a
机器人与视觉标定理论详解
CDx= cos (a) * (Cx0-X0) – sin (a) * (Cy0-Y0) + X1 – Cx0
= (cos (a) -1) * (Cx0-X0) – sin (a) * (Cy0-Y0) + MDx
= (cos (a) -1) * StDx- sin (a) * StDy+ MDx
CDy= cos (a) * (Cy0-Y0) + sin (a) * (Cx0-X0) + Y1 – Cy0
= (cos (a) -1) * (Cy0-Y0) + sin (a) * (Cx0-X0) + Mdy
= (cos (a) -1) * StDy + sin (a) * StDx + Mdy
从公式中可以看出StDx = Cx0-X0,StDy = Cy0-Y0是个常量,MDx和Mdy是每次拍照是工件(Mark)的坐标与标准位置工件(Mark)的差值;
StDx与StDy怎么计算呢?蓝色的为一个二元一次方程,我们需要旋转一个角度即可计算出;
如果计算出StDx和StDy则在运行时,直接带入上述公式,可以很快计算出CDx,Cdy这样给出Robot的偏移量了,而不需要计算旋转中心的确切坐标了;
如何求解StDx和StDy
StDx,StDy计算过程,首先Robot在拍照点旋转一定角度a(一定是Robot给出)
机器人与视觉标定理论详解
CDx= cos (a) * (Cx0-X0) – sin (a) * (Cy0-Y0) + X1 – Cx0
= (cos (a) -1) * (Cx0-X0) – sin (a) * (Cy0-Y0) + MDx
= (cos (a) -1) * StDx- sin (a) * StDy+ MDx
CDy= cos (a) * (Cy0-Y0) + sin (a) * (Cx0-X0) + Y1 – Cy0
= (cos (a) -1) * (Cy0-Y0) + sin (a) * (Cx0-X0) + Mdy
= (cos (a) -1) * StDy + sin (a) * StDx + Mdy
下面介绍如何求解StDx和StDy,旋转一定角度a后MDx和Mdy则为确定值,cos(a)和sin(a)为确定值
0= (cos (a) -1) * StDx- sin (a) * StDy+ MDx
0= (cos (a) -1) * StDy + sin (a) * StDx + Mdy
StDx = -0.5*(Mdx*(cos(a)-1)+Mdy*sin(a)) / (1-cos(a))
StDy = 0.5*(Mdx*sin(a)-Mdy*(cos(a)-1))/(1-cos(a))
a是旋转标准的角度
Mdx=X1-X0,即旋转后Mark坐标与训练模板的mark坐标
声明:部分内容来源于网络,仅供读者学术交流之目的。文章版权归原作者所有。如有不妥,请联系。