人工智能-实验三

第三次实验

一.实验目的

​ 掌握分类算法的算法思想，包括朴素贝叶斯算法，决策树算法等。编写朴素贝叶斯算法进行分类操作。本实验主要是关于朴素贝叶斯算法的实现，在完成本实验时也复习了课程中学习的决策树分类算法的思想。

二.实验原理

1.条件概率与贝叶斯公式

​ 条件概率是指事件A在另外一个事件B已经发生条件下的发生概率，记为P(A|B)。若只有两个事件A和B，则：
$$P(A|B)=\frac{P(AB)}{P(B)}$$
​ 由条件概率公式可得出贝叶斯公式：
$$\begin{gathered} P(AB)=P(A|B)P(B) \\ P(B|A)=\frac{P(AB)}{P(A)}=\frac{P(A|B)P(B)}{P(A)} \end{gathered}$$
​ 贝叶斯公式常用于已知事件发生，求导致事件发生的各种原因的概率。

2.朴素贝叶斯分类算法

​ 朴素贝叶斯分类算法是基于贝叶斯定理和特征条件独立性假设的分类方法。对于给定的训练集，基于特征条件独立性假设学习输入输出的联合概率分布(先验概率和条件概率分布)，学习概率分布后，利用贝叶斯定理求出后验概率最大的输出作为预测结果。

​ 模型训练的过程相当于学习P(Ai|B)，其中B是特定的类别，Ai是特征。计算该概率时，假设各个特征之间互不影响，每个特征都是条件独立的。这个假设就是条件独立性假设，可以简化朴素贝叶斯方法，但可能牺牲一定的分类准确性。

​ 模型预测的过程就是根据贝叶斯公式求P(B|Ai)的概率，即在有各个特征的条件下，预测输入属于哪一个分类的概率，属于哪一个分类的概率最大，就预测输入样本的类别是哪一类。根据贝叶斯公式，P(B|Ai)被转换为：
$$P(B|Ai)=\frac{P(Ai|B)P(B)}{P(Ai)}$$
​ 由于对于每个类别，计算公式都有分母P(Ai)，因此只需要计算分子并比较大小就可以了，按照条件独立性假设，转换为：
$$P(B)P(A_1|B)P(A_2|B)..P(A_n|B)$$
​ 而P(Ai|B)就是模型训练时计算得到的条件概率。

3.决策树算法

​ 决策树是一个预测模型，树中每个节点表示某个对象，而每个分叉路径则代表某个可能的属性值，而每个叶节点则对应从根节点到该叶节点所经历的路径表示根据属性值进行决策的一个完整过程。

​ 常见的决策树算法有ID3，C4.5，CART算法。在本课程中重点学习的是ID3算法。ID3算法使用信息增益作为属性的选择标准，确定生成每个节点采用的属性。

​ 信息熵用于衡量数据集的纯度，定义为：

​ 假设A是样本的一个属性，A有v个取值，将训练数据集划分为V份，每个子集有pi个正例和ni个反例，则条件熵计算如下。
$$H(D|A)=\sum _{i=1}^v\frac{pi+ni}{p+n}H([\frac{pi}{pi+ni},\frac{ni}{pi+ni}])$$
​ 信息增益是指集合D的信息熵与特征A给定条件下的信息条件熵之差：
$$Gain(D,A)=H(D)-H(D|A)$$
​ 构建决策树时，希望选择的决策属性能尽可能的起到分类的作用，即要使分类后集合的纯度尽可能高，即H(D|A)越小越好，因此选择信息增益最大的属性作为当前层次的分类决策。完成当前层次的属性选择后，再计算剩余属性的信息增益，重复上述过程，直到所有属性都被选择或所有样本都已经完成分类，就完成了整颗决策树的构建。而分类的只需要从决策树的根节点开始，根据节点的属性选择左右分支，直到到达叶子节点，就得到了分类结果。

三.实验内容

1.朴素贝叶斯算法

​ 假设A表示类别，B，C，D表示三个特征。根据朴素贝叶斯算法的原理，所求概率为：
$$P(A|BCD)=\alpha P(A)P(B|A)P(C|A)P(D|A)$$
训练

​ 约定朴素贝叶斯算法使用的条件概率计算结果存储结构为：

#类别的先验概率
self.label_prob =　{类别:概率} 
#每个类别下特征为某个取值的条件概率
self.condition_prob = {}
#内部结构为：类别(好/坏)：{特征编号：{特征取值：条件概率}}

​ 计算需要用到的概率，首先计算各个类别在训练样本中出现了多少个，除总样本数得到P(A)：

        #计算label_prob
        cnt = 0
        num = 0
        for item in label:
            num+=1
            if item == 1:
                cnt+=1
        self.label_prob[0] = (num-cnt)/num
        self.label_prob[1] = cnt/num

​ 接下来从初始化两个类别下，保存特征取值概率的字典：

		self.condition_prob[0] = {}
        self.condition_prob[1] = {}
        #初始化每个特征取值的字典
        for item in self.condition_prob:
            for feat in range(len(feature[0])): #len(feature[0])为特征数量
                self.condition_prob[item][feat] = {}

​ 遍历所有样本的特征，并进行每个特征取值的计数：

        i=0         #样本编号
        for data in feature:
            j=0     #特征序号
            for feat in data:
                if(self.condition_prob[0][j].get(feat)==None):
                    self.condition_prob[0][j][feat] = 0
                if(self.condition_prob[1][j].get(feat)==None):
                    self.condition_prob[1][j][feat] = 0
                if label[i]==0:
                    self.condition_prob[0][j][feat] += 1
                else:
                    self.condition_prob[1][j][feat] += 1
                j+=1
            i+=1

​ 最后除以每个类别的样本数量，得到条件概率：

        for feat in range(len(feature[0])):
            for item in self.condition_prob[0][feat]:
                self.condition_prob[0][feat][item] /= (num-cnt)
            for item in self.condition_prob[1][feat]:
                self.condition_prob[1][feat][item] /= cnt

预测

​ 预测的过程只需要按照贝叶斯公式进行计算，由于分类只有两种(好/坏)，只需要分别计算：
$$\begin{gathered} P(A_{good})=\alpha P(A_{bad})P(B|A_{bad})P(C|A_{bad})P(D|A_{bad}) \\ P(A_{bad})=\alpha P(A_{bad})P(B|A_{bad})P(C|A_{bad})P(D|A_{bad}) \end{gathered}$$
​ B，C，D的取值是输入样本的特征值，进行预测计算的过程如下：

    def predict(self, feature):
        '''
        对数据进行预测，返回预测结果
        :param feature:测试数据集所有特征组成的ndarray
        :return:
        '''
        res = []
        for item in feature:
            P_good = self.label_prob[1]
            P_bad = self.label_prob[0]
            feat_idx = 0
            for feat in item:
                P_good *= self.condition_prob[1][feat_idx][feat]
                P_bad *= self.condition_prob[0][feat_idx][feat]
                feat_idx+=1
            if P_good>P_bad:
                res.append(1)
            else:
                res.append(0)
        return res

2.拉普拉斯平滑

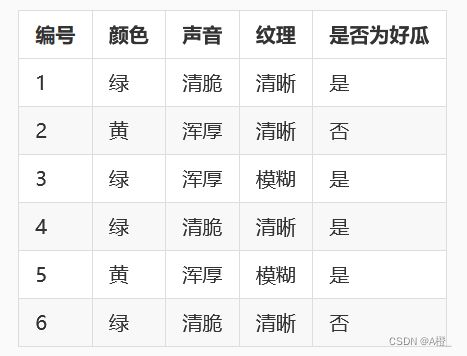
​ 如果样本不够多，可能存在某些分类不存在特定特征，这样在利用朴素贝叶斯算法进行分类时，如果出现了这个特征，预测就不合理了。如下例：

​ 坏瓜类别中，没有纹理特征为模糊的样本，则P(模糊|坏瓜)的概率为0，如果预测的样本中出现了纹理特征为模糊，计算出的概率中，是坏瓜的概率就是0。为此要进行平滑处理，最常用的方法是拉普拉斯平滑。

​ 拉普拉斯平滑指的是，假设N表示训练数据集总共有多少种类别，Ni表示训练数据集中第i列总共有多少种取值。则训练过程中在算类别的概率时分子加1，分母加N，算条件概率时分子加1，分母加Ni。

​ 即P(Ai)修正为：
$$P(Ai)=\frac{类别为Ai的样本数+1}{样本数+N}$$
​ 而P(Bj|Ai)修正为：
$$P(Bj|Ai)=\frac{类别是Ai的且特征B为Bj的样本数量+1}{类别是Ai的样本数+Ni(特征B的取值种类数)}$$
​ 修正后的概率和条件概率不会为0，避免了上述不合理的情况。

​ 根据拉普拉斯平滑原理，计算类别概率的过程修改为：

        cnt = 0
        num = 0
        for item in label:
            num+=1
            if item == 1:
                cnt+=1
        types = 2	#类别数
        self.label_prob[0] = (num-cnt)+1/(num+types)
        self.label_prob[1] = cnt+1/(num+types)

​ 存储条件概率的字典初始化不需要修改，仍为：

        self.condition_prob[0] = {}
        self.condition_prob[1] = {}
        #初始化每个特征取值的字典
        for item in self.condition_prob:
            for feat in range(len(feature[0])):
                self.condition_prob[item][feat] = {}

​ 计算条件概率时，调整分子和分母，实现拉普拉斯平滑：

        #记录每个特征的取值
        i=0         #样本编号
        for data in feature:
            j=0     #特征序号
            for feat in data:
                if(self.condition_prob[0][j].get(feat)==None):
                    self.condition_prob[0][j][feat] = 1     #分子加一，初始化为1
                if(self.condition_prob[1][j].get(feat)==None):
                    self.condition_prob[1][j][feat] = 1     #分子加一，初始化为1
                if label[i]==0:
                    self.condition_prob[0][j][feat] += 1
                else:
                    self.condition_prob[1][j][feat] += 1
                j+=1
            i+=1
        #计算条件概率，每个特征取值 除 label为0和1的个数+特征的取值种类数
        for feat in range(len(feature[0])):
            for item in self.condition_prob[0][feat]:
                self.condition_prob[0][feat][item] /= (num-cnt)+len(self.condition_prob[0][feat])
            for item in self.condition_prob[1][feat]:
                self.condition_prob[1][feat][item] /= cnt+len(self.condition_prob[1][feat])

​ 预测的过程不变，仍按照贝叶斯公式计算，取在给定特征下，属于特定类别的概率最大的类别作为分类结果。

3.实验结果

​ 在没有拉普拉斯平滑的情况下，对给定数据预测准确率高于0.8。进行拉普拉斯平滑处理后，对给定数据预测准确率高于0.9。

4.思考题

​ 朴素贝叶斯算法实现比较简单，没有参数，但是条件独立性假设可能牺牲预测的准确性。

​ 决策树算法(ID3)没有剪枝策略，信息增益策略可能对取值数多的特征有所偏好(更能降低熵值)，而类似编号的特征会使信息增益接近于1.并且只能处理离散分布的特征。在ID3的基础上，C4.5算法使用信息增益率作为分类属性的选择标准，避免了ID3对特征数目的偏重。并且引入了剪枝策略进行剪枝，将连续特征进行离散化(取相邻两样本的平均值作为划分点，计算各个划分点作为分类点时的信息增益)

​ 对于支持向量机算法和人工神经网络等算法可以通过增加迭代次数或减小学习率来提高模型训练的效果，提高性能。