【电机应用控制】——步进电机控制原理(四相五线/两相四线/细分驱动)&驱动器&梯形/S形加减速算法&直线/圆弧插补
目录
一、步进电机简介
二、步进电机控制原理
1.四相五线
2.两相四线
3.细分驱动
三、步进电机驱动器
四、梯形加减速算法
五、S形加减速算法
六、直线插补
七、圆弧插补
八、步进电机闭环系统(位置闭环)
总结
前言
声明:学习笔记来自B站正点原子教程,仅供学习交流!!
一、步进电机简介
步进电机是一种把电脉冲信号转换为角位移(左)或线位移(右)的电动机。
步距角:两相通常1.8°,三相通常1.2°、无相通常0.72°,角位移=脉冲个数X步距角。
在非超载且不超频的情况下,电机的旋转位置只取决于脉冲个数,转速只取决脉冲信号的频率。所以只需要统计脉冲个数和频率,不再需要编码器测速和位置,具有优秀的开环能力,当然也可接编码器反馈速度和位置数据,实现更加精准的闭环控制。
分类:
按照磁激励进行分类:永磁式、反应式(磁阻式)、混合式:
永磁式动态性能好,输出力矩大,但步距角大通常7.5°;反应式(磁阻式)结构简单成本低,步距角小一般1.2°,但振动噪音大动态性能差;混合式的转子铁芯上有很多齿,可实现很小步距角,运动顺滑,且力矩大动态性能好,应用最广泛,但结构复杂价格高。
按相数区分:相数是指电机内部的线圈的组数,常用的有二相、三相、四相、五相:
一组线圈就是一相,两组就是两相,以此类推,一组线圈是一根导线绕成。
如下图四相五线:5是1、2、3、4线圈的公共端,所以是四组线圈(有的路是重合的);引出五条线头。5的极性是一定的比如接GND,那么电流就只能1到5、2到5、3到5、4到5单向,所以这种电机也叫做单极性步进电机:
如下图两相四线:电流方向是双向的,也叫做双极性步进电机。右图绿色为一根线绕成,红色为一根线绕成,是两组线圈。
二、步进电机控制原理
1.四相五线
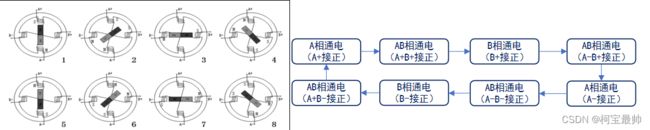
下图为四相五线步进电机(单极性),+为公共端,分A、B、C、D四相。
单极性整步驱动(单线圈通电):
单极性整步驱动,(双线圈通电,磁场强度更大、力矩更大):
单极性半步驱动,转子每次走半步,旋转更顺滑:
2.两相四线
下图是两相四线步进电机(双极性)
双极性整步驱动(单线圈通电,磁铁NS极两端都受力,所以力矩比单极性大)
双极性整步驱动(双线圈通电,力矩更大)
双极性半步驱动(可实现更小步距角)
但是这样步距角还是很大,可以在硬件上增加相数,增加极齿,但这样有限,可以采用软件方式控制电流实现步距角细分。
3.细分驱动
细分驱动:将步距角以电流分配方法进行细分化的技术。一般电机产品都会集成这种技术,使用时只需细分数即可实现。
原理:磁场强度和电流大小成正比。如果Ia = Ib 那么转子将停在相邻两个线圈的中间,如果不相等,转子将停在电流较大的一侧;通过改变输入电流的比例,就可以比原来更小的步距角进行驱动;可进行超微小角度,更加平滑的运转,有效地降低振动和噪音的驱动方法。
静态指标:
相数:线圈的组数,两相步进电机步距角一般为 1.8°,三相的步进电机步距角为 1.2°,相数越多步距角越小。
步距角:一个脉冲信号所对应的电机转动的角度,这个步距角他不一定是电机实际工作的真正步距角,真正的步距角与驱动器的细分有关。
拍数:完成一个磁场周期性变化所需的脉冲数。
定位转矩:电机在不通电状态下,电机转子自身的锁定力矩(由磁场齿形的谐波以及机械误差造成的)。
动态指标:
步距角精度:步进电机转动一个步距角度的实际值与理论值的误差。用百分比表示:误差/步距角 *100%。
失步:电机运转的步数,不等于理论上的步数。也可以叫做丢步,一般都是因负载过大或者是频率过快。
最大空载起动频率:不加负载的情况下,能够直接起动的最大频率。
最大空载运行频率:电机不带负载的最高转速频率。
运行距频特性:输出转矩与输入脉冲频率的关系,是电机选型的根本依据。要在该曲线之下才能保证运行时不丢步。
电机正反转控制:改变通电顺序而改变电机的正反转。
三、步进电机驱动器
控制定子绕组周期性、交替得电,进而控制步进电机一步一步的向前运动的这个控制器就是步进电机驱动器。有细分功能的步进驱动器可以改变步进电机的固有步距角,达到更大的控制精度、降低振动及提高输出转矩。
以正点原子步进电机驱动器 ATK-2MD5050为例:
特点:采用12~50VDC 供电, 输出峰值电流可达 5.0A, 适合驱动常用的 42mm、 57mm、86mm 两相混合式步进电机,超高分辨率微步进,最大支持 256 细分。适用场景:3D 打印机、雕刻机、数控机床、包装机械等分辨率要求较高的设备。
左图右侧中间为SW1-SW8参数设定,下面是拨码开关,在这里设置细分数和电流。注意使用拨码开时要断开电源。驱动器有共阳极和共阴极两种接线方法,如下图为共阳极接到控制器Vcc,使能信号、方向信号和脉冲信号低电平有效:
引脚介绍:
使能引脚ENA-、ENA+:当此信号有效时,驱动器将自动切断电机绕组电流,使电机处于自由状态(无保持转矩),也叫脱机引脚。
方向引脚DIR+、DIR-:此信号有效时,电机顺时针旋转,无效时电机逆时针旋转。
脉冲引脚PUL+、PUL-:每接收一个脉冲,驱动步进电机旋转一个步距角,脉冲频率与转速成正比。
电机接线端子A+、A-、B+、B-:A+和A-是步进电机的A相绕组的两个接线柱;B+和B-是步进电机的B相绕组的两个接线柱。
硬件接口介绍:(正点原子的F4开发板)
连接使能和方向引脚的是普通光耦,连接脉冲引脚的是高速光耦(中间蓝色)。光耦可防止外部电流倒灌,损坏芯片,还有增强驱动能力的作用。
四、梯形加减速算法
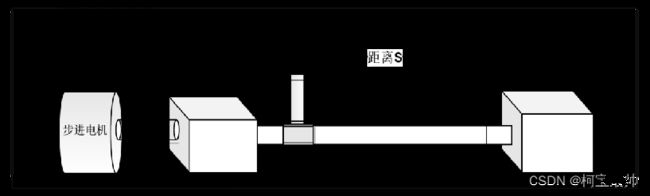
如下图使用步进电机实现物体X的移动,系统要求物体X从A点出发,到B点停止,移动的时间越短越好且系统稳定。使用梯形加减速可使系统稳定:
实现原理:(注意哪些是用户规定已知的)
算法分析:
下次脉冲周期T最难求(注意T是一系列值得统称,T即下图的δt),其次是加减速段步数。在程序中用的是反转时间,反转两次才是一个完整脉冲周期T,所以程序用时要把T除以2。
下次脉冲周期T求解
t1 :发送第二个脉冲的时刻 。t2 :发送第三个脉冲的时刻 。δt :两个脉冲之间的间隔时间。c0 :定时器从 t0~t1 时刻的定时器计数值 。c1 :定时器从 t1~t2 时刻的定时器计数值。tt为定时器计数周期,即计数频率的倒数,计数频率=基本频率/分频值。所以求T也即求出:c0、 c1、c2…cn。
①加速/减速阶段
已知条件:ft 是定时器的计数频率 ;α 是步距角;Spr 是步进电机旋转一圈脉冲数(电机相关常数 );θ 表示位置; ω 表示速度 ;n 是脉冲数。
计数值C的计算需连续两次开根号,实时运动中比较费时,使用泰勒公式的特例——麦克劳林公式进行优化。在化简时舍弃了无穷小余项,当n=1时有0.4485的偏差,我们可以将C0乘一个系数0.676来解决这个误差:
在加速和减速过程中都需要重新计算下一步的时间 。但是计算过程中可能有除不尽的数,所以需要另外把余数部分加上去(提高间隔时间的精度和准确性)
②匀速阶段
在匀速阶段速度值是我们设置的所以已知,ft定时器的计数频率已知,步距角已知,所以可以求得匀速阶段时的计数值,我们这里定义一个:A_T_x10
加减速段步数求解(即脉冲数n)
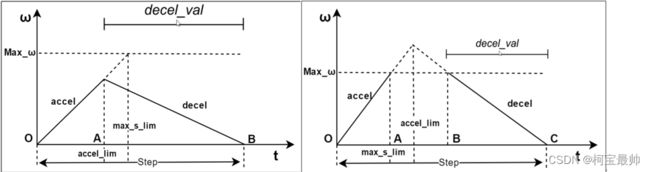
在加速过程中,有两种场景计算速度属性: 未达到最大速度就要开始减速(左);持续加速直到我们设置的最大速度(匀速阶段)(右)
需要推导出加减速度与步数n的关系
①左图:最大速度偏大,加速度偏小,max_s_lim >= accel_lim
由图可知初速度为0,加速段末速度与减速段的初速度相等,t1为加速段整个过程消耗的时间,t2则是减速度过程消耗的时间:
 ②右图:最大速度偏小,加速度偏大,max_s_lim < accel_lim
②右图:最大速度偏小,加速度偏大,max_s_lim < accel_lim
最后结果只有decel_val减速段步数不一样,其他两个一样:
整体流程梳理:
定时器中断处理流程
定时器中断产生步脉冲并且只有在步进电机移动时进入,四个不同运动的状态,分别是stop——accel——run——decel——stop,如图:
梯形加减速流程图&中断流程图(上图的详细版)
五、S形加减速算法
简介:
在加减速的变化过程中速度曲线呈现一个英文字母“S”形的,我们称之为S形加减速算法。S形加减速在启动停止以及高速运动时的速度变化的比较慢,导致冲击力噪音就很小,所以更适用于精密的工件搬运与建造。而梯形加减速更适合一些定长送料的场合。
S形加减速分七段式和五段式算法,7段式具有平稳、精度高的特点,但该算法的参数复杂,大大降低到了工作效率且对硬件的要求较高;5段式算法简单、具有实时性和高精度的加减速控制算法,非常适合资源紧凑的小型嵌入式系统:
我们主要介绍五段式算法,T1加加速、T2减加速、T3匀速、T4加减速、T5减减速五个阶段
基本结论:加加速度的开始点和结束点为零,加速度的斜率是相同的,所以T1=T2,T4=T5;加速度的变化率(J)相等只是方向相反;加速段位移和减速段位移算法一样,只是速度排序是倒序。
原理与梯形加减速类比即可:
算法分析:
加速段位移和减速段位移算法一样,只是速度排序是倒序。所以需要求:加加速阶段步数、减加速阶段步数、下一脉冲周期T。
步数即脉冲数,也即对应位移,求出位移表达式即可得到每个时间点对应的脉冲数;下一个脉冲周期T=Cn*tt=Cn/ft(即计数量*计数一次的时间),所以求T,也即求Cn。根据速度表达式可以换算成step/s的单位,而一步对应一个完整脉冲(两次翻转),此时就可将step/s换算成2次翻转(一个脉冲周期)/s,易得T与速度v互为倒数。
①加加速阶段步数求解
②减加速阶段步数求解
③确定下一个脉冲周期
首先需将设定速度单位rpm转换为step/s,这样既可表示1秒内可步进多少步数;而且速度v的倒数 1/V 单位就为s/step(每一步对应的时间)直接对应要输出脉冲的周期。两相步进电机的步距角1.8°,360°需要200step,但驱动器设置了8细分,需要1600step,即360°对应1600步。
1rpm=1圈/min=360°/min=1600step/min=1600/60(step/s)
T=Cn*tt=Cn/ft=1/Vn则Cn=ft/Vn
流程是先通过位移公式知道第一步时间t1,当S = 1时,此时t1为第一步的时间知道第一步所需的时间t1,通过t1计算出下一步的速度V,速度的倒数1/V,就是第二步脉冲的周期… …
基本流程:
①用户设置参数:设置总步数Step、加速段总时间以及减速段总时间、最大速度
②求解未知量:根据已知量,求解中点速度、加速度、加加速段步数以及减加速段步数等等
③生成速度表:将设置S = 1,计算第一步的时间值以及速度值,并计算出速度表
④实现第一步:通过速度表,求第一步的C值,设置定时器比较值以及开启脉冲输出,中断使能
⑤中断服务函数:通过速度表得到每一步的定时器计数值,判断当前运动状态,分别是加速段、匀速段、减速段、和停止状态
至此,以上的都是步进电机的一维问题,但除了一维还有多维即多轴联动,下面我们介绍有关步进电机二维控制的知识!
六、直线插补
简介:
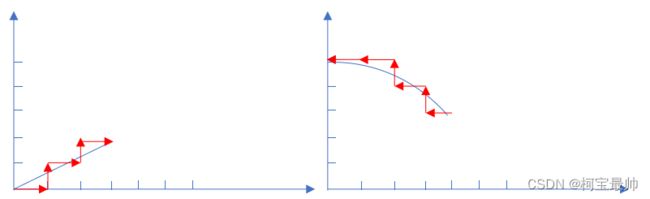
沿规定轮廓,计算起点与终点之间的若干个坐标点,以微小的直线段(单位向量)运动逼近。 插补实质就是进行数据点的密化工作。这里介绍二维的,需要两个步进电机,xy轴单位向量不一定相同。
这里我们只学习脉冲增量插补算法中的逐点比较法。脉冲增量式插补:通过向各个运动轴分配驱动脉冲来控制机床坐标轴协调运动,从而加工出一定轮廓形状的算法。逐点比较:每走一步都将加工点的瞬时坐标同规定的图形轨迹比较,判断其偏差,决定下一步的走向。逐点比较法就是用来确定往哪个轴分配驱动脉冲。
插补原理:
设直线终点坐标A(Xe,Ye),动点P(Xi,Yi)。
①如果P点在直线上那么Yi / Xi = Ye / Xe ,即取偏差判别式:F = Xe*Yi – Xi*Ye = 0。
②当P点在直线上方那么有Yi / Xi > Ye / Xe,即: F = Xe*Yi – Xi*Ye > 0。
③当P点在直线下方那么有Yi / Xi < Ye / Xe, 即: F = Xe*Yi – Xi*Ye < 0。
当F > 0,+X向进一步,当F < 0,+Y向进一步 当F = 0,满足Xe ≥ Ye,+X向进一步,否则+Y向进一步。
插补步骤:
①偏差判别:根据偏差函数值判别加工点的相对直线距离
②坐标进给:沿减小误差的方向进给一步
③偏差计算:进给后,计算新加工点相对直线的位置
④终点判别:判别是否到达终点,未到达则继续第一步步骤,继续插补,到终点则停止
递推算法:简化偏差计算,已知,偏差工程式:F(Xi,Yi) = Xe*Yi – Xi*Ye。
若下一步向+X步进,此时 Xi = Xi+1,Yi = Yi:
若下一步向+Y步进,此时 Xi = Xi,Yi = Yi+1:
终点判别:
总步长法:将终点位置的x,y坐标相加求和,得出总步数,开始插补时,无论是往哪个轴给进一步,总步数都减一,直到为0时,代表已到终点,就停止插补。
第一象限&任意象限插补:
任意象限插补方法都可以用第一象限推出,用|X|和|Y|代替X和Y即可。不同象限的坐标进给方向由坐标值的符号确定,前面就多了个正反转判别。
代码实现思路:
①初始化定时器:初始化IO,设置ARR、PSC,计数方式以及脉冲输出模式等。
②电机旋转方向判断:实现任意象限直线插补,需提前判断所属象限,设置电机旋转方向。
③编写直线插补算法:实现插补第一步,偏差判别,坐标进给,偏差计算并开启脉冲输出与中断使能。
④编写中断服务函数:实现除第一步以外的其他步数的偏差判别、坐标进给、偏差计算、终点判别。
七、圆弧插补
在圆弧起点与终点间,计算逼近实际圆弧的点群,控制刀具沿点运动,加工出圆弧曲线。
插补原理:
设要加工图形为第一象限逆时针走向的圆弧AE,半径为R,以原点为圆心,动点P(Xi,Yi)。
①当P点在圆弧上,就有关系: Xi²+Yi² = R²,即偏差判别式:F = Xi²+Yi²-R² = 0
②当P点在圆弧外的话,就有: Xi²+Yi² > R²,即:F = Xi²+Yi²-R² > 0
③当P点在圆弧内的话,就有: Xi²+Yi² < R²,即: F = Xi²+Yi²-R² < 0
结论:当F ≥ 0,-X向进一步,即向圆内走一步;当F < 0,+Y向进一步,即向圆弧外走一步。
插补步骤:
流程与直线插补一样,偏差计算也有一个简化过程,终点判断也采用总步长法。
偏差计算简化:由已知加工偏差判别式: F = Xi²+Yi²-R²,
①当动点P(Xi,Yi)在圆弧上或圆弧外,F ≥ 0,需向X轴负方向进给一步(-X),此时新加工点P的位置:X = Xi-1,Y = Yi,此时加工偏差为:
![]() ②当动点P在圆弧内侧的话,F < 0,需向y轴正向进给一步(+Y),此时新加工点P的位置:X = Xi,Y = Yi+1,此时加工偏差为:
②当动点P在圆弧内侧的话,F < 0,需向y轴正向进给一步(+Y),此时新加工点P的位置:X = Xi,Y = Yi+1,此时加工偏差为:
终点判别:也是总步长法, 在插补处理开始之前,先设置一个总步长计数器n =|Xe - Xa|+ |Ye - Ya|。其中,圆弧终点坐标E(Xe,Ye),起点坐标A(Xa,Ya),插补过程中,无论向那个轴进给一步,总步数都减一,直到总步数为0时,代表已到终点,停止插补计算。
第一象限&任意象限插补:
代码实现思路:
①初始化定时器:初始化IO,设置ARR、PSC,计数方式以及脉冲输出模式等。
②设置圆弧方向:需提前设置好是顺圆弧还是逆圆弧
③电机旋转方向判断:实现任意象限圆弧插补,需提前判断所属象限,设置电机旋转方向。
④编写圆弧插补算法:实现插补第一步,偏差判别,坐标进给,偏差计算并开启脉冲输出与中断使能。
④编写中断服务函数:计算动点新坐标,实现除第一步以外的其他步数的偏差判别、坐标进给、偏差计算、终点判别。
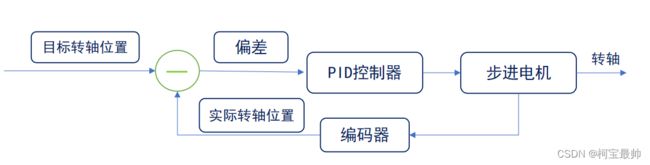
八、步进电机闭环系统(位置闭环)
闭环系统的组成:步进电机+编码器,编码器反馈步进电机的实际旋转位置
位置环PID代码实现思路:
①初始化定时器:初始化IO,设置ARR、PSC,计数方式以及脉冲输出模式等
②编码器接口模式:初始化编码器接口模式,用来采集反馈信号
③PID算法实现:实现增量式/位置式PID算法,调整好比例P,积分I,微分D的参数
④位置环运动控制:设置电机旋转方向,以及对PID控制器输出的期望值,作用到电机运动
⑤编写中断服务函数:编码器溢出计数,定时控制电机,设置比较值
STM32&keil实操......
总结
遇到挫折,要有勇往直前的信念,马上行动,坚持到底,决不放弃,成功者决不放弃,放弃者绝不会成功。成功的道路上,肯定会有失败;对于失败,我们要正确地看待和对待,不怕失败者,则必成功;怕失败者,则一无是处,会更失败。
今天的学习分享到此就结束了,我们下次再见!!
往期精彩:
控制理论 PID算法
STM32定时器输入捕获(IC)
STM32定时器输出比较(PWM波)
STM32定时中断
STM32外部中断
STM32GPIO精讲
…