最短路径问题——基于Dijkstra算法和Floyd算法的最短路径问题
目录
1、算法介绍
(1)Dijkstra Algorithm(迪杰斯特拉算法)
(2)Floyd Algorithm(佛洛依德算法)
(3)两种算法区别
2、问题描述
3、完整代码
4、运行结果截图
1、算法介绍
(1)Dijkstra Algorithm(迪杰斯特拉算法)
迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止。
基本思想
通过Dijkstra计算图G中的最短路径时,需要指定起点s(即从顶点s开始计算)。
此外,引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度),而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。
初始时,S中只有起点s;U中是除s之外的顶点,并且U中顶点的路径是"起点s到该顶点的路径"。然后,从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 然后,再从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 ... 重复该操作,直到遍历完所有顶点。
操作步骤
(1) 初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为"起点s到该顶点的距离"[例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞。
(2) 从U中选出"距离最短的顶点k",并将顶点k加入到S中;同时,从U中移除顶点k。
(3) 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。
(4) 重复步骤(2)和(3),直到遍历完所有顶点。
(2)Floyd Algorithm(佛洛依德算法)
求解赋权图中每对顶点间的最短距离。
Floyd算法是经典的动态规划算法,基本思想是递推产生一个矩阵序列A1,A2,.....,Ak,...,An(图有n个节点),Ak=(ak(i,j))nxn。其中矩阵Ak第i行第j列表示从顶点vi到顶点vj的路径上经过的顶点序号不大于k的最短路径长度。
迭代公式:![]()
k是迭代次数,i,j,k=1,2......n。
当最后k=n是时,An矩阵就是各个顶点之间的最短距离值了。
(3)两种算法区别
迪杰斯特拉算法是求特定顶点到其它顶点的距离,而佛洛依德算法则是求所有顶点之间的距离。
2、问题描述
以物流中心选址为例,已知定点①、②、③、④, 各点间的费用如图所示在四个点中选定一个点为物流的中心使得该点到其他每个点的费用是最小的,完成该选址问题的算法实现。
Dijkstra算法在物流的配送运输中能够合理的进行决策和分析而Flody算法比较适合选择合理的物流中心从而使物流的总费用达到最少的效果。
模型如下:
3、完整代码
#include
#define MaxVerNum 100 //顶点最大数目值
#define VexType char //顶点数据类型
#define EdgeType int //弧数据类型
#define M 10000 //作为最大值
using namespace std;
//图的邻接矩阵表示法
typedef struct Graph
{
VexType Vex[MaxVerNum]; //顶点数组
EdgeType Edge[MaxVerNum][MaxVerNum]; //弧表
int vexnum, arcnum; //顶点数、弧数
}Graph;
//迪杰斯特拉算法全局变量
bool S[MaxVerNum]; //顶点集
int D[MaxVerNum]; //到各个顶点的最短路径
int Pr[MaxVerNum]; //记录前驱
//弗洛伊德算法全局变量
int F_D[MaxVerNum][MaxVerNum]; //Floyd的D矩阵 记录最短路径
int P[MaxVerNum][MaxVerNum];//最短路径记录矩阵
//初始化函数
void InitGraph(Graph &G)
{
memset(G.Vex, '#', sizeof(G.Vex));//初始化顶点表 void *meset(void *s,int ch,size_t n)
for (int i = 0; i < MaxVerNum; i++)//初始化弧表 memset(结构体/数组名 , "用于替换的字符“ , 前n个字符 )
for (int j = 0; j < MaxVerNum; j++)
G.Edge[i][j] = M;
G.arcnum = G.vexnum = 0; //初始化顶点数、弧数
}
//插入点函数
bool InsertNode(Graph &G, VexType v)
{
if (G.vexnum < MaxVerNum)
{
G.Vex[G.vexnum++] = v;
return true;
}
return false;
}
//插入弧函数
bool InsertEdge(Graph &G, VexType v, VexType w, int weight)
{
int p1, p2;//v,w两点下标
p1 = p2 = -1;//初始化
for (int i = 0; i F_D[i][k] + F_D[k][j])
{
F_D[i][j] = F_D[i][k] + F_D[k][j]; //F_D[][]记录最短路径值
P[i][j] = k; //P[][]记录最短路径
}
bool flag = true; //判断有无负圈
for (int l = 0; l < G.vexnum; l++)
for (int j = 0; j < G.vexnum; j++)
if (l==j&&F_D[l][j] < 0)
{
flag = false;
break;
}
return flag;
}
//输出最短路径
void Path(Graph G, int v)
{
if (Pr[v] == -1)
return;
Path(G, Pr[v]);
cout << G.Vex[Pr[v]] << "->";
}
// 输出Floyd最短路径 v是终点
void F_Path(Graph G, int v, int w)
{
cout << "->"<< G.Vex[P[v][w]] ;
if (P[v][w] == -1)
return;
F_Path(G, v,P[v][w]);
}
//打印图的顶点表
void PrintVex(Graph G)
{
for (int i = 0; i < G.vexnum; i++)
{
cout << G.Vex[i] << "\t";
}
cout << endl;
}
//打印图的弧矩阵
void PrintEdge(Graph G)
{
for (int i = 0; i < G.vexnum; i++)
{
for (int j = 0; j < G.vexnum; j++)
{
if (G.Edge[i][j] == M)cout << "∞" << "\t";
else cout << G.Edge[i][j] << " " << "\t";
}
cout << endl;
}
}
//创建图功能实现函数
void CreateGraph(Graph &G)
{
VexType v, w;
int vn, an;//顶点数,弧数
cout << "请输入物流中心数目:" << endl;
cin >> vn;
cout << "请输入路径数目:" << endl;
cin >> an;
cout << "请输入所有物流中心名称:" << endl;
for (int i = 0; i> v;
if (InsertNode(G, v)) continue;
else {
cout << "输入错误!" << endl; break;
}
}
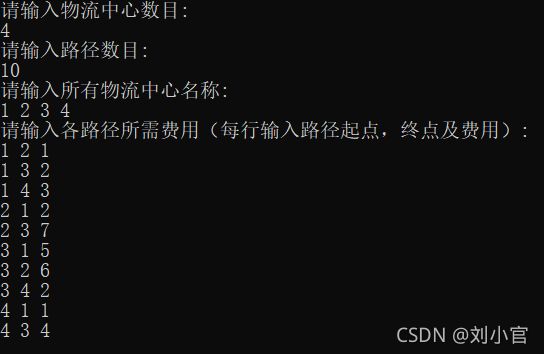
cout << "请输入各路径所需费用(每行输入路径起点,终点及费用):" << endl;
for (int j = 0; j> v >> w >> weight;
if (InsertEdge(G, v, w, weight)) continue;
else {
cout << "输入错误!" << endl; break;
}
}
system("cls");
cout << "录入成功!";
}
//打印图的邻接矩阵
void PrintGraph(Graph &G)
{
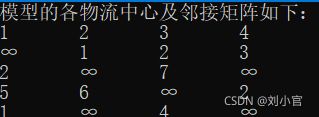
cout << "模型的各物流中心及邻接矩阵如下:" << endl;
PrintVex(G);
PrintEdge(G);
}
//调用最短路径-Dijkstra算法
void Shorted_Dijkstra(Graph &G)
{
char vname;
int v = -1;
cout << "请输入物流中心起点名称:" << endl;
cin >> vname;
for (int i = 0; i < G.vexnum; i++)
if (G.Vex[i] == vname)v = i;
if (v == -1)
{
cout << "没有找到该起点!" << endl;
return;
}
Dijkstra(G, v);//调用函数
cout << "目标中心" << "\t" << "最少费用" << "\t" << "所走路径" << endl;
for (int j = 0; j < G.vexnum; j++)
{
if (j != v)
{
cout << " " << G.Vex[j] << "\t" << " " << D[j] << "\t" << "\t";
Path(G, j);//打印路径
cout << G.Vex[j] << endl;
}
}
}
//调用最短路径- Floyd算法
void Shorted_Floyd(Graph &G)
{
if (Floyd(G))//调用函数
{
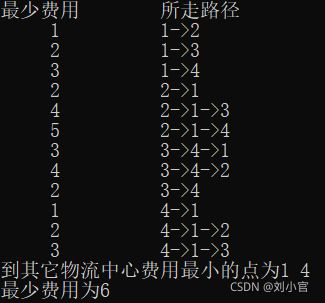
cout << "最少费用" << "\t" << "所走路径" << endl;
for (int i = 0; i < G.vexnum; i++)
for (int j = 0; j < G.vexnum; j++)
{
if( i == j) continue;
cout << " "< " << endl;
cout << "************ 1.构造选址模型 ************" << endl;
cout << "************ 2.打印选址模型 ************" << endl;
cout << "************ 3.迪杰斯特拉(Dijkstra) ************" << endl;
cout << "************ 4.弗洛伊德(Floyd) ************" << endl;
cout << "************ 0.退出模拟 ************" << endl;
cout < 4、运行结果截图
操作界面:
构造选址模型:
邻接矩阵:
转载请注明出处 ,并附有原文链接,如有侵权,请及时联系。