OpenCV实战(25)——3D场景重建
OpenCV实战(25)——3D场景重建
-
- 0. 前言
- 1. 重建 3D 场景
-
- 1.1 3D 场景点重建
- 1.2 算法原理
- 2. 分解单应性
- 3. 光束平差法
- 4. 完整代码
- 小结
- 系列链接
0. 前言
在《相机姿态估计》一节中,我们学习了如何在校准相机时恢复观察 3D 场景的相机的位置。算法应用了以下事实,即有时场景中可见的某些 3D 点的坐标可能是已知的。而如果能够从多个角度观察场景,即使没有关于 3D 场景的信息可用,也可以重建 3D 姿势和结构。在本节中,我们将使用不同视图中图像点之间的对应关系来推断 3D 信息,同时介绍一个新的数学实体用于校准相机的两个视图之间的关系,并将讨论三角测量的原理以便从 2D 图像重建 3D 点。
1. 重建 3D 场景
我们使用校准后的相机,拍摄两张场景照片,然后使用 SIFT (Scale Invariant Feature Transform) 检测器和描述符来匹配这两个视图之间的特征点。
相机的校准参数为我们在世界坐标系中的计算奠定了基础,需要在相机姿态和相应点的位置之间建立物理约束。我们引入了一个新的数学实体,本质矩阵 (essential matrix),它基本矩阵的校准版本, cv::findEssentialMat 函数可用于计算本质矩阵,估计图像中的投影关系。
我们可以使用已建立的点对应调用 cv::findEssentialMat 函数,并通过随机抽样一致算法 (RANdom SAmple Consensus, RANSAC) 算法过滤掉异常点以保留符合找到的几何形状的匹配项。
1.1 3D 场景点重建
(1) 首先,使用 SIFT 检测器和描述符在每个图像中获取关键点:
// 关键点和描述符向量
std::vector<cv::KeyPoint> keypoints1;
std::vector<cv::KeyPoint> keypoints2;
cv::Mat descriptors1, descriptors2;
// SIFT特征检测器
cv::Ptr<cv::Feature2D> ptrFeature2D = cv::xfeatures2d::SIFT::create(500);
// SIFT 特征及其描述符
ptrFeature2D->detectAndCompute(image1, cv::noArray(), keypoints1, descriptors1);
ptrFeature2D->detectAndCompute(image2, cv::noArray(), keypoints2, descriptors2);
(2) 使用 cv::BFMatcher 匹配使用描述符检测到的关键点并将它们存储为浮点数:
// 匹配两张图像的描述符
// 带有交叉检查的匹配器
cv::BFMatcher matcher(cv::NORM_L2, true);
// 匹配
std::vector<cv::DMatch> matches;
matcher.match(descriptors1, descriptors2, matches);
// 将关键点转换为 Point2f
std::vector<cv::Point2f> points1, points2;
for (std::vector<cv::DMatch>::const_iterator it = matches.begin();
it != matches.end(); ++it) {
float x = keypoints1[it->queryIdx].pt.x;
float y = keypoints1[it->queryIdx].pt.y;
points1.push_back(cv::Point2f(x, y));
x = keypoints2[it->trainIdx].pt.x;
y = keypoints2[it->trainIdx].pt.y;
points2.push_back(cv::Point2f(x, y));
}
(3) 使用 cv::findEssentialMat 函数,获得两个图像中匹配的图像关键点的相机矩阵:
// 图像 1 和图像 2 之间的本质矩阵
cv::Mat inliers;
cv::Mat essential = cv::findEssentialMat(
points1, points2,
cMatrix, // 固有参数
cv::RANSAC, 0.9, 1.0, // RANSAC 方法
inliers);
生成的 inliers 匹配集如下:

(4) 基本矩阵封装了两个视图的旋转和平移组件。因此,可以直接从这个矩阵中恢复两个视图之间的相对姿态,这可以利用 OpenCV 函数 cv::recoverPose 完成:
// 从本质矩阵中恢复相对相机姿态
cv::Mat rotation, translation;
cv::recoverPose(essential, // 本质矩阵
points1, points2, // 匹配关键点
cameraMatrix, // 内在矩阵
rotation, translation, // 姿态估计
inliers); // inliers 匹配
(5) 有了两个相机之间的相对位姿,可以估计我们在两个视图之间建立对应关系的点的位置。下图显示了两台摄像机的估计位置(左边的一台位于原点)。我们选择一对对应点,并根据投影几何模型,追踪对应于相关 3D 点所有可能位置的一条射线:
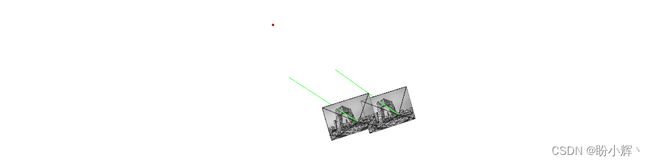
由于这两个图像点是由同一个 3D 点生成的,所以两条射线必定会相交于 3D 点所在位置。当两个相机的相对位置已知时,将两个对应图像点的投影线相交的方法称为三角测量 (triangulation)。这个过程首先需要两个投影矩阵,并且可以重复应用于所有匹配,但必须使用世界坐标表示。可以通过使用 cv::undistortPoints 函数来完成以上过程。
(6) 最后,调用 triangulate 函数计算三角点的位置:
// 由 R, T 组成投影矩阵
cv::Mat projection2(3, 4, CV_64F); // 3x4 投影矩阵
rotation.copyTo(projection2(cv::Rect(0, 0, 3, 3)));
translation.copyTo(projection2.colRange(3, 4));
// 合成通用投影矩阵
cv::Mat projection1(3, 4, CV_64F, 0.); // 3x4 投影矩阵
cv::Mat diag(cv::Mat::eye(3, 3, CV_64F));
diag.copyTo(projection1(cv::Rect(0, 0, 3, 3)));
// inliers
std::vector<cv::Vec2d> inlierPts1;
std::vector<cv::Vec2d> inlierPts2;
// 为三角测量创建 inliers 输入点向量
int j(0);
for (int i = 0; i < inliers.rows; i++) {
if (inliers.at<uchar>(i)) {
inlierPts1.push_back(cv::Vec2d(points1[i].x, points1[i].y));
inlierPts2.push_back(cv::Vec2d(points2[i].x, points2[i].y));
}
}
// 矫正并归一化图像点
std::vector<cv::Vec2d> points1u;
cv::undistortPoints(inlierPts1, points1u, cameraMatrix, cameraDistCoeffs);
std::vector<cv::Vec2d> points2u;
cv::undistortPoints(inlierPts2, points2u, cameraMatrix, cameraDistCoeffs);
// 三角测量
std::vector<cv::Vec3d> points3D;
triangulate(projection1, projection2, points1u, points2u, points3D);
(7) 计算得到位于场景元素上的 3D 点,如下所示:
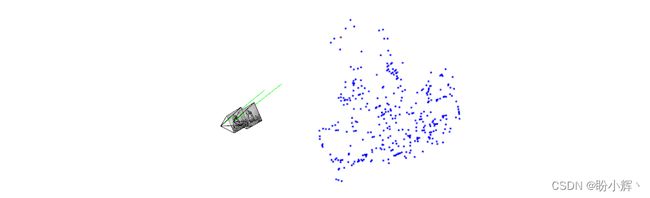
需要注意的是,在上图的角度来看,我们绘制的两条射线并没有按照预期相交。
1.2 算法原理
校准矩阵可以用于将像素坐标转换为世界坐标。应用该矩阵可以将图像点与产生它们的 3D 点相关联。在下图中演示了物理世界点与其图像之间的关系:
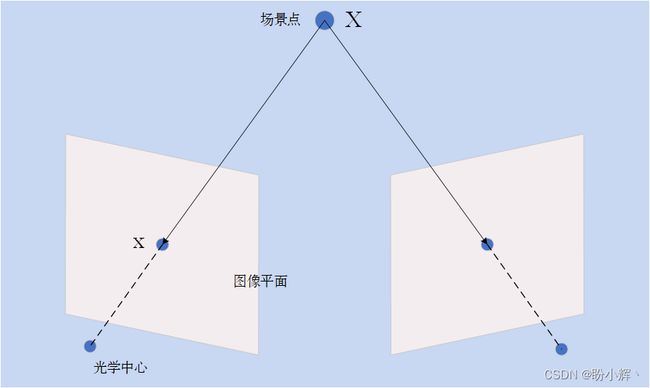
上图显示了由旋转 R R R 和平移 T T T 变换的两个相机,平移向量 T T T 连接了两个相机的投影中心,还有一个 x x x 向量将第一个相机中心连接到一个图像点,以及一个 x ′ x' x′ 向量将第二个相机中心连接到相应的图像点。由于有两个相机之间的相对位置,我们可以根据第二个相机参考将 x x x 的方向表示为 R x R_x Rx。观察所示图像点的几何形状,可以发现 T T T、 R x R_x Rx 和 x ′ x' x′ 向量都共面,可以用以下数学方程表示这种情况:
x ′ ⋅ ( T × R x ) = x ′ E x = 0 x'\cdot(T\times R_x)=x'Ex=0 x′⋅(T×Rx)=x′Ex=0
可以将第一个关系简化为一个 3x3 矩阵 E E E,因为叉积也可以通过矩阵运算来表示。这个 E E E 矩阵被称为本质矩阵,相关的方程是校准的对极约束。我们可以根据图像对应估计这个基本矩阵,计算过程与基本矩阵类似,区别在于需要使用世界坐标计算。此外,基本矩阵是根据两个相机之间的旋转和平移分量构建的,一旦估计了这个矩阵,就可以对其进行分解以获得相机之间的相对位姿。以上过程可以使用 cv::recoverPose 函数实现。cv::recoverPose 函数会调用 cv::decomposeEssentialMat 函数,cv::decomposeEssentialMat 函数为相对姿势生成四种可能的解,通过计算一组匹配来确定正确的解,从而确定物理上的可能解。
一旦获得了相机之间的相对位姿,就可以通过三角测量恢复与匹配对对应的点的位置。三角剖分问题最简单的解决方案需要考虑两个投影矩阵 P P P 和 P ′ P' P′,在齐次坐标中寻找 3D 点可以表示为 X = [ X , Y , Z , 1 ] T X=[X,Y,Z,1]^T X=[X,Y,Z,1]T,因为我们已经知道 x = P X x=PX x=PX 和 x ′ = P ′ X x'=P'X x′=P′X。这两个齐次方程决定了两个独立方程,足以解决 3D 点位置的三个未知数。这个超定方程系统可以使用最小二乘法求解,以上过程可以通过 OpenCV 函数 cv::solve 完成:
// 使用线性LS方法进行三角测量
cv::Vec3d triangulate(const cv::Mat &p1,
const cv::Mat &p2,
const cv::Vec2d &u1,
const cv::Vec2d &u2) {
// 假设方程组image=[u,v], X=[X,y,z,1],其中u(p3.X)=p1.X和v(p3.X)=p2.X
cv::Matx43d A(u1(0)*p1.at<double>(2, 0) - p1.at<double>(0, 0), u1(0)*p1.at<double>(2, 1) - p1.at<double>(0, 1), u1(0)*p1.at<double>(2, 2) - p1.at<double>(0, 2),
u1(1)*p1.at<double>(2, 0) - p1.at<double>(1, 0), u1(1)*p1.at<double>(2, 1) - p1.at<double>(1, 1), u1(1)*p1.at<double>(2, 2) - p1.at<double>(1, 2),
u2(0)*p2.at<double>(2, 0) - p2.at<double>(0, 0), u2(0)*p2.at<double>(2, 1) - p2.at<double>(0, 1), u2(0)*p2.at<double>(2, 2) - p2.at<double>(0, 2),
u2(1)*p2.at<double>(2, 0) - p2.at<double>(1, 0), u2(1)*p2.at<double>(2, 1) - p2.at<double>(1, 1), u2(1)*p2.at<double>(2, 2) - p2.at<double>(1, 2));
cv::Matx41d B(p1.at<double>(0, 3) - u1(0)*p1.at<double>(2, 3),
p1.at<double>(1, 3) - u1(1)*p1.at<double>(2, 3),
p2.at<double>(0, 3) - u2(0)*p2.at<double>(2, 3),
p2.at<double>(1, 3) - u2(1)*p2.at<double>(2, 3));
// X 包含重建点的三维坐标
cv::Vec3d X;
// 求解 AX=B
cv::solve(A, B, X, cv::DECOMP_SVD);
return X;
}
在上一小节得到的结果图像中我们已经看到,由于噪声和数字化的影响,预期应该相交的投影线实际上并不相交。因此,最小二乘解会在交点附近得到解。此外,如果尝试在无穷远处重建一个点,则此方法并不起作用,这是因为,对于这样的点,齐次坐标的第四个元素应该为 0 而不是 1。
最后,重要的是需要知道比例因子才能完成 3D 重建,如果需要进行实际测量,至少需要知道一个物理距离,例如,两个相机之间的实际距离或某一物体的高度。
3D 重建是计算机视觉中一个重要的研究领域,接下来,我们介绍在 OpenCV 库中相关的一些其他内容。
2. 分解单应性
在本节中,我们了解到可以分解通过一个基本矩阵恢复两个相机之间的旋转和平移分量。我们知道平面的两个视图之间存在单应性,该单应性还包含旋转和平移分量。此外,它还包含有关平面的信息,即它相对于每个相机的法线。cv::decomposeHomographyMat 函数可以用来分解这个矩阵;但是,我们需要有一台校准过的相机。
3. 光束平差法
在本节中,我们首先从匹配中估计相机位置,然后通过三角测量重建关联的 3D 点。可以通过使用任意数量的视图来完成这个过,检测每一视图的特征点并将其与其他视图匹配。基于此,可以得到与视图、3D 点集和校准信息之间的旋转和平移相关方程。所有这些未知数都可以通过优化过程一起优化,优化过程旨在最小化每个视图中所有可见点的重投影误差。这种组合优化过程称为捆集调整或光束平差法 (bundle adjustment)。cv::detail::BundleAdjusterReproj 类实现了相机参数计算算法,其最小化重投影误差平方之和。
4. 完整代码
头文件 (triangulate.h) 完整代码如下所示:
#include 主函数文件 (estimateE.cpp) 完整代码如下所示:
#include 小结
3D 重建是计算机视觉中一个重要的研究领域,在本节中,我们使用不同视图中图像点之间的对应关系来推断 3D 信息,使用 cv::findEssentialMat 函数计算本质矩阵,并介绍了三角测量的原理以从 2D 图像重建 3D 点。
系列链接
OpenCV实战(1)——OpenCV与图像处理基础
OpenCV实战(2)——OpenCV核心数据结构
OpenCV实战(3)——图像感兴趣区域
OpenCV实战(4)——像素操作
OpenCV实战(5)——图像运算详解
OpenCV实战(6)——OpenCV策略设计模式
OpenCV实战(7)——OpenCV色彩空间转换
OpenCV实战(8)——直方图详解
OpenCV实战(9)——基于反向投影直方图检测图像内容
OpenCV实战(10)——积分图像详解
OpenCV实战(11)——形态学变换详解
OpenCV实战(12)——图像滤波详解
OpenCV实战(13)——高通滤波器及其应用
OpenCV实战(14)——图像线条提取
OpenCV实战(15)——轮廓检测详解
OpenCV实战(16)——角点检测详解
OpenCV实战(17)——FAST特征点检测
OpenCV实战(18)——特征匹配
OpenCV实战(19)——特征描述符
OpenCV实战(20)——图像投影关系
OpenCV实战(21)——基于随机样本一致匹配图像
OpenCV实战(22)——单应性及其应用
OpenCV实战(23)——相机标定
OpenCV实战(24)——相机姿态估计