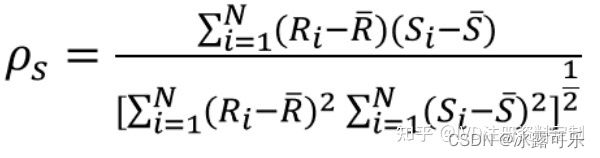复盘：pearson皮尔森相关系数和spearman斯皮尔曼相关系数的区别

复盘：pearson皮尔森相关系数和spearman斯皮尔曼相关系数的区别

提示：系列被面试官问的问题，我自己当时不会，所以下来自己复盘一下，认真学习和总结，以应对未来更多的可能性

关于互联网大厂的笔试面试，都是需要细心准备的
（1）自己的科研经历，科研内容，学习的相关领域知识，要熟悉熟透了
（2）自己的实习经历，做了什么内容，学习的领域知识，要熟悉熟透了
（3）除了科研，实习之外，平时自己关注的前沿知识，也不要落下，仔细了解，面试官很在乎你是否喜欢追进新科技，跟进创新概念和技术
（4）准备数据结构与算法，有笔试的大厂，第一关就是手撕代码做算法题
面试中，实际上，你准备数据结构与算法时以备不时之需，有足够的信心面对面试官可能问的算法题，很多情况下你的科研经历和实习经历足够跟面试官聊了，就不需要考你算法了。但很多大厂就会面试问你算法题，因此不论为了笔试面试，数据结构与算法必须熟悉熟透了
秋招提前批好多大厂不考笔试，直接面试，能否免笔试去面试，那就看你简历实力有多强了。

---

pearson和spearman的区别

相关系数是用以反映变量之间的相关关系程度的统计指标。

其取值范围是[-1,1]，
当取值为0时表示不相关，
取值为[-1,0)表示负相关，
取值为(0,1]，表示正相关。

目前常用的两种相关性系数为皮尔森相关系数（Pearson）和斯皮尔曼等级相关系数（Spearman）

皮尔森相关系数评估两个连续变量之间的线性关系

其中：

-1 ≤ p ≤ 1
p接近0代表无相关性
p接近1或-1代表强相关性

斯皮尔曼相关系数评估两个连续变量之间的单调关系。

在单调关系中，变量趋于一起变化，但不一定以恒定速率变化。

N是观测值的总数量

斯皮尔曼另一种表达公式：也是最常用的更好理解的表达式

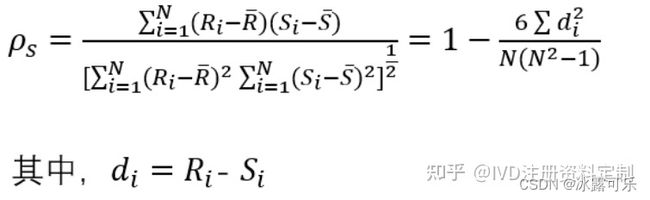
表示二列成对变量的等级差数。

区别

Pearson和Spearman相关系数的范围可以从-1到+1。

当Pearson相关系数为+1时，意味着，当一个变量增加时，另一个变量增加一致量。
这形成了一种递增的直线。
在这种情况下，Spearman相关系数也是+1。

如果关系是一个变量在另一个变量增加时增加，但数量不一致，
则Pearson相关系数为正但小于+1。

但是在这种情况下，斯皮尔曼系数仍然等于+1。

Pearson=+ 0.851，Spearman=+1

当关系是随机的或不存在时，则两个相关系数几乎为零。

Pearson=-0.093，Spearman=-0.093

如果关系递减的直线，那么两个相关系数都是-1。

Pearson=-1，Spearman=-1

如果关系是一个变量在另一个变量增加时减少，但数量不一致，
则Pearson相关系数为负但大于-1。

但是在这种情况下，斯皮尔曼系数仍然等于-1

Pearson=-0.799，Spearman=-1

相关值-1或1意味着精确的线性关系，如圆的半径和圆周之间的关系。

然而，相关值的实际价值在于量化不完美的关系。
发现两个变量是相关的经常通知回归分析，该分析试图更多地描述这种类型的关系。

其他非线性关系

Pearson相关系数仅评估线性关系。

Spearman相关系数仅评估单调关系。

因此，即使相关系数为0，也可以存在有意义的关系。
检查散点图以确定关系的形式。

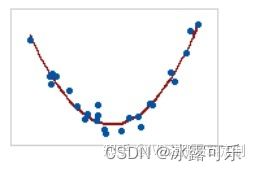
系数为0

该图显示了非常强的关系。

Pearson系数和Spearman系数均约为0。

结论

皮尔森评估的是两个变量的线性关系，而斯皮尔曼评估的两变量的单调关系。

Pearson 处理变量的数据原始值，而 Spearman 处理数据排序值（需要先做变换，transform）

因此，斯皮尔曼相关系数对于数据错误和极端值的反应不敏感。

如果散点图表明“可能是单调的，可能是线性的”关系，
最好的选择是 Spearman 而不是 Pearson。

即使数据证明是完全线性的，用 Spearman 也不会造成信息丢失。

但是，如果不是完全线性但使用 Pearson 系数，会丢失 Spearman 可以捕获的信息，是否单调。

---

总结

提示：重要经验：

1）皮尔森评估的是两个变量的线性关系，而斯皮尔曼评估的两变量的单调关系
2）Pearson 处理变量的数据原始值，而 Spearman 处理数据排序值（需要先做变换，transform）
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。