四种进制介绍及转换
一、进制介绍
1、对于整数,有四种表示方式(Java):
二进制:0,1 ,满 2 进 1.以 0b 或 0B 开头;
十进制:0-9 ,满 10 进 1(是我们日常使用的数值);
八进制:0-7 ,满 8 进 1. 以数字 0 开头表示;
十六进制:0-9 及 A(10)-F(15),满 16 进 1. 以 0x 或 0X 开头表示。此处的 A-F 不区大小写
代码演示:
//二进制(以0b或0B开头的数值)
int n1 = 0b1010;
//八进制(以0开头的数值)
int n2 = 01010;
//十进制(就是我们正常使用的进制数)
int n3 = 1010;
//十六进制(以0x或0X开头的数值)
int n4 = 0x1010;2、四种进制映射关系图示:
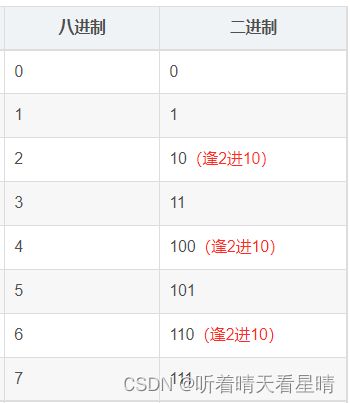
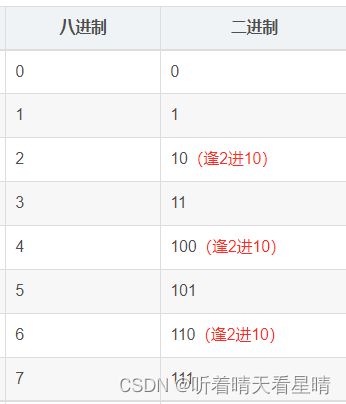
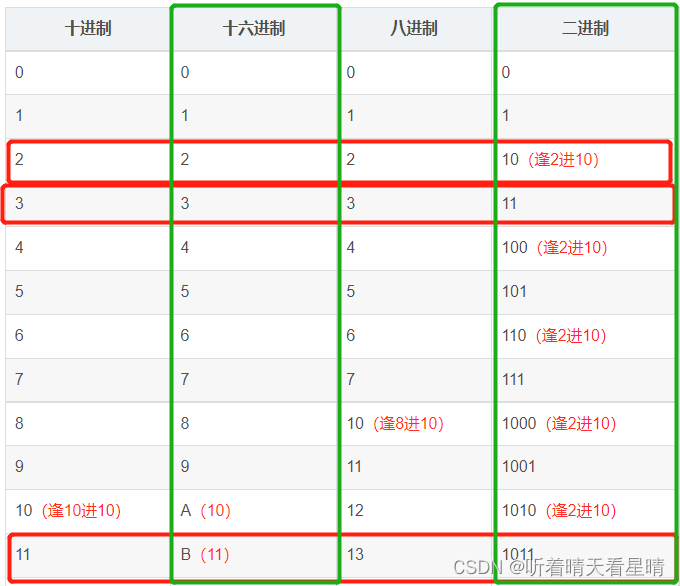
以十进制为基准,从0到17每一种进制分别对应的数值,其实就是从0开始每一种数值向下加1,按其逢满多少往高位进10(也就是进1位)的原则自然累加展示,比如自然数到9加1就是10原理都是一样
| 十进制 | 十六进制 | 八进制 | 二进制 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 10(逢2进10) |
| 3 | 3 | 3 | 11 |
| 4 | 4 | 4 | 100(逢2进10) |
| 5 | 5 | 5 | 101 |
| 6 | 6 | 6 | 110(逢2进10) |
| 7 | 7 | 7 | 111 |
| 8 | 8 | 10(逢8进10) | 1000(逢2进10) |
| 9 | 9 | 11 | 1001 |
| 10(逢10进10) | A(10) | 12 | 1010(逢2进10) |
| 11 | B(11) | 13 | 1011 |
| 12 | C(12) | 14 | 1100(逢2进10) |
| 13 | D(13) | 15 | 1101 |
| 14 | E(14) | 16 | 1110(逢2进10) |
| 15 | F(15) | 17 | 1111 |
| 16 | 10(逢16进10) | 20(逢8进10) | 10000(逢2进10) |
| 17 | 11 | 21 | 10001 |
二、四种进制的相互转换
我们这里分为四组来学习
1. 第一组:(其他三种进制转十进制)
二进制转十进制
规则:从最低位(右边)开始,将每一位上的数提取出来,乘以2的(位数-1)次方,最后求和,其中位数就是代表当前数从右边数第几位,类如:1011中的0在第3位,它的位数就是3
示例:将0b1011转成十进制数
0b1011=1*2的(1-1)次方 + 1*2的(2-1)次方 + 0*2的(3-1)次方 + 1*2的(4-1)次方
=1*2^0 + 1*2^1 + 0*2^2 + 1*2^3
=1+2+0+8
=11
八进制转十进制
规则:从最低位(右边)开始,将每一位上的数提取出来,乘以8的(位数-1)次方,最后求和,其中位数就是代表当前数从右边数第几位
示例:将0234转成十进制数
0234 = 4*8^0 + 3*8^1 + 2*8^2
=4 +24 + 128
=156
十六进制转十进制
规则:从最低位(右边)开始,将每一位上的数提取出来,乘以16的(位数-1),最后求和,其中位数就是代表当前数从右边数第几位
示例:将0x23A转成十进制数
0x23A = 10 * 16^0 + 3 * 16 ^ 1 + 2 * 16^2
= 10 + 48 + 512
= 570
2.第二组:(十进制转其他三种进制)
十进制转二进制
规则:将该数不断除以 2,直到商为 0 为止,然后将每步得到的余数倒过来,就是对应的二进制。
示例:将34转成二进制
注意:在计算机程序中使用的就是二进制数,而计算机的基本单位就是字节,而一个字节占8位二进制数,因此上图示例得出的100010不满八位时,计算机会默认往前添置对应的位数0,比如00100010
十进制转八进制
规则:将该数不断除以 8,直到商为 0 为止,然后将每步得到的余数倒过来,就是对应的八进制。
示例:131 转成八进制 => 0203
十进制转十六进制
规则:将该数不断除以 16,直到商为 0 为止,然后将每步得到的余数倒过来,就是对应的十六进制
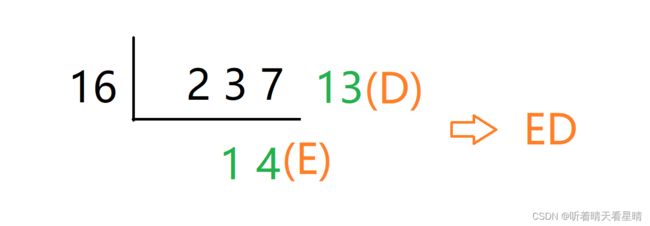
示例:请将 237 转成十六进制 => 0xED
3.第三组:(二进制转八进制和十六进制)
二进制转八进制
有两种方式:
1、可以将二进制转十进制,然后再将十进制转八进制
示例:请将 ob11010101 转成八进制
先将二进制转十进制:
11010101 = 1*2^0+0*2^1+1*2^2+0*2^3+1*2^4+0*2^5+1*2^6+1*2^7
=1+ 0 + 4 + 0 + 16 + 0 + 64 + 128
=213
再将十进制转八进制
213/8 = 26...5
26/8 = 3...2
=> 325
最终转为八进制java中表示0325
2、通过上方四种进制0-17映射关系,我们可以从低位(右边)开始,将二进制数每三位一组,转成对应的八进制数即可
示例:请将 ob11010101 转成八进制
将11 010 101每三位为一组按照图表映射关系进行转换
101 = 5
010 = 2
11 = 011 = 3
最终为 0325
二进制转十六进制
有两种方式:请将 0b11010101 转成十六进制
1、可以将二进制转十进制,然后再将十进制转十六进制
先将二进制转成我们熟悉的十进制
1101 0101 = 1*2^0 + 0*2^1 + 1*2^2 + 0*2^3 + 1*2^4 + 0*2^5 + 1*2^6 + 1*2^7
= 1 + 0 + 4 + 0 + 16 + 0 + 64 + 128
= 213
再将十进制转成16进制
213/16 = 13(D)......5
=> 0xD5
2、从低位开始,将二进制数每四位为一组,按照四种进制0-17映射关系,转成对应的十六进制数即可
将1101 0101每四位为一组按照图标映射关系进行转换
0101 = 5
1101 = 13 = D
=> 0xD5
4.第四组(八进制和十六进制转二进制)
八进制转二进制
规则:将八进制数每 1 位数,按照映射关系转成对应的一个 3位数二进制数,必须是是3位的二进制数,其实就是将二进制转八进制的第二种方法的一个逆向操作,如图所示
示例:请将 0237 转成二进制数
237 => 010 011 111 = 10 011 111(去除前面补齐的0)
2 = 010
3 = 011
7 = 111
十六进制转二进制
规则:将十六进制数每 1 位数,按照映射关系转成对应的一个 4位数二进制数,必须是是4位的二进制数,其实就是将二进制转十六进制的第二种方法的一个逆向操作,如图所示
示例:请将 0x23B 转成二进制数
0x23B => 0010 0011 1011 = 10 0011 1011 (去除前面补齐的0)
2 = 0010
3 = 0011
B = 11 = 1011
*注: 以上转换后的结果含有前置0或多个0的只是针对计算机按字节补位来展示的