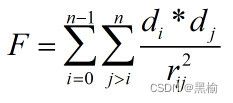比较18个3*6尺寸差值结构的迭代次数

已发现二值化差值结构有3种相互作用，纵向，横向和斜向。纵向相互作用只与行间距有关而与数值的数量无关，与迭代次数成反比；横向相互作用只与列的数值数量有关与列间距无关，与迭代次数成正比；斜向相互作用将导致行分布与列分布与差值结构之间的1对多的关系。

这里比较了18个不同的差值结构的迭代次数，他们都只有纵向和横向相互作用，没有斜向相互作用。在行分布与列分布确定的情况下只有唯一的差值结构与之对应。因此有理由认为行分布与列分布携带了差值结构的所有信息，可以仅通过比较行分布与列分布去比较迭代次数。

( A, B )---3*30*2---( 1, 0 )( 0, 1 )

让网络的输入只有3个节点，AB训练集各由6张二值化的图片组成，让A中有6个1，B中全是0.比较迭代次数的顺序

差值结构			A-B	迭代次数		行分布								列分布				行排斥力		平均列							列排斥力
1	1	1	7*1*4*2*0*0-0*0*0*0*0*0	3106.407	d	0	0	1	1	1	1	a		2	2	2		9		0	0	9	9	9	9		292.5
0	0	1	7*1*4*2*0*0-0*0*0*0*0*0	3106.407
1	0	0	7*1*4*2*0*0-0*0*0*0*0*0	3106.407
0	1	0	7*1*4*2*0*0-0*0*0*0*0*0	3106.407
0	0	0	7*1*4*2*0*0-0*0*0*0*0*0	3106.407
0	0	0	7*1*4*2*0*0-0*0*0*0*0*0	3106.407
1	1	0	6*4*2*4*2*0-0*0*0*0*0*0	3367.935	d	0	1	1	1	1	1	a		3	3	0		9		0	9	9	9	9	9		407.8125
1	0	0	6*4*2*4*2*0-0*0*0*0*0*0	3367.935
0	1	0	6*4*2*4*2*0-0*0*0*0*0*0	3367.935
1	0	0	6*4*2*4*2*0-0*0*0*0*0*0	3367.935
0	1	0	6*4*2*4*2*0-0*0*0*0*0*0	3367.935
0	0	0	6*4*2*4*2*0-0*0*0*0*0*0	3367.935
1	1	0	6*4*4*4*2*0-0*0*0*0*0*0	3476.296	d	0	1	1	1	1	1	a		4	2	0		8		0	8	8	8	8	8		322.2222
1	0	0	6*4*4*4*2*0-0*0*0*0*0*0	3476.296
1	0	0	6*4*4*4*2*0-0*0*0*0*0*0	3476.296
1	0	0	6*4*4*4*2*0-0*0*0*0*0*0	3476.296
0	1	0	6*4*4*4*2*0-0*0*0*0*0*0	3476.296
0	0	0	6*4*4*4*2*0-0*0*0*0*0*0	3476.296
0	1	1	3*4*4*2*1*0-0*0*0*0*0*0	4038.91	d	0	1	1	1	1	1	a		2	2	2		9		0	9	9	9	9	9		407.8125
1	0	0	3*4*4*2*1*0-0*0*0*0*0*0	4038.91
1	0	0	3*4*4*2*1*0-0*0*0*0*0*0	4038.91
0	1	0	3*4*4*2*1*0-0*0*0*0*0*0	4038.91
0	0	1	3*4*4*2*1*0-0*0*0*0*0*0	4038.91
0	0	0	3*4*4*2*1*0-0*0*0*0*0*0	4038.91
1	1	1	7*1*1*2*0*0-0*0*0*0*0*0	4086.126	d	0	0	1	1	1	1	a		3	2	1		8.75		0	0	8.75	8.75	8.75	8.75		276.4757
0	0	1	7*1*1*2*0*0-0*0*0*0*0*0	4086.126
0	0	1	7*1*1*2*0*0-0*0*0*0*0*0	4086.126
0	1	0	7*1*1*2*0*0-0*0*0*0*0*0	4086.126
0	0	0	7*1*1*2*0*0-0*0*0*0*0*0	4086.126
0	0	0	7*1*1*2*0*0-0*0*0*0*0*0	4086.126
1	1	0	6*6*2*4*0*0-0*0*0*0*0*0	5254.709	d	0	0	1	1	1	1	a		3	3	0		9		0	0	9	9	9	9		292.5
1	1	0	6*6*2*4*0*0-0*0*0*0*0*0	5254.709
0	1	0	6*6*2*4*0*0-0*0*0*0*0*0	5254.709
1	0	0	6*6*2*4*0*0-0*0*0*0*0*0	5254.709
0	0	0	6*6*2*4*0*0-0*0*0*0*0*0	5254.709
0	0	0	6*6*2*4*0*0-0*0*0*0*0*0	5254.709
1	1	1	7*5*2*0*0*0-0*0*0*0*0*0	6307.814	d	0	0	0	1	1	1	a		2	2	2		9		0	0	0	9	9	9		182.25
1	0	1	7*5*2*0*0*0-0*0*0*0*0*0	6307.814
0	1	0	7*5*2*0*0*0-0*0*0*0*0*0	6307.814
0	0	0	7*5*2*0*0*0-0*0*0*0*0*0	6307.814
0	0	0	7*5*2*0*0*0-0*0*0*0*0*0	6307.814
0	0	0	7*5*2*0*0*0-0*0*0*0*0*0	6307.814
0	1	1	3*4*1*1*1*0-0*0*0*0*0*0	9720.759	d	0	1	1	1	1	1	a		4	1	1		6		0	6	6	6	6	6		181.25
1	0	0	3*4*1*1*1*0-0*0*0*0*0*0	9720.759
0	0	1	3*4*1*1*1*0-0*0*0*0*0*0	9720.759
0	0	1	3*4*1*1*1*0-0*0*0*0*0*0	9720.759
0	0	1	3*4*1*1*1*0-0*0*0*0*0*0	9720.759
0	0	0	3*4*1*1*1*0-0*0*0*0*0*0	9720.759
1	1	1	7*2*2*2*0*0-0*0*0*0*0*0	11051.61	d	0	0	1	1	1	1	a		4	1	1		6		0	0	6	6	6	6		130
0	1	0	7*2*2*2*0*0-0*0*0*0*0*0	11051.61
0	1	0	7*2*2*2*0*0-0*0*0*0*0*0	11051.61
0	1	0	7*2*2*2*0*0-0*0*0*0*0*0	11051.61
0	0	0	7*2*2*2*0*0-0*0*0*0*0*0	11051.61
0	0	0	7*2*2*2*0*0-0*0*0*0*0*0	11051.61
0	1	1	3*3*2*2*0*0-0*0*0*0*0*0	12238.71	d	0	0	1	1	1	1	a		4	2	0		8		0	0	8	8	8	8		231.1111
0	1	1	3*3*2*2*0*0-0*0*0*0*0*0	12238.71
0	1	0	3*3*2*2*0*0-0*0*0*0*0*0	12238.71
0	1	0	3*3*2*2*0*0-0*0*0*0*0*0	12238.71
0	0	0	3*3*2*2*0*0-0*0*0*0*0*0	12238.71
0	0	0	3*3*2*2*0*0-0*0*0*0*0*0	12238.71
0	1	1	3*2*2*2*2*0-0*0*0*0*0*0	12367.27	d	0	1	1	1	1	1	a		5	1	0		5		0	5	5	5	5	5		125.8681
0	1	0	3*2*2*2*2*0-0*0*0*0*0*0	12367.27
0	1	0	3*2*2*2*2*0-0*0*0*0*0*0	12367.27
0	1	0	3*2*2*2*2*0-0*0*0*0*0*0	12367.27
0	1	0	3*2*2*2*2*0-0*0*0*0*0*0	12367.27
0	0	0	3*2*2*2*2*0-0*0*0*0*0*0	12367.27
1	1	1	7*5*4*0*0*0-0*0*0*0*0*0	12466.59	d	0	0	0	1	1	1	a		3	2	1		8.75		0	0	0	8.75	8.75	8.75		172.2656
1	0	1	7*5*4*0*0*0-0*0*0*0*0*0	12466.59
1	0	0	7*5*4*0*0*0-0*0*0*0*0*0	12466.59
0	0	0	7*5*4*0*0*0-0*0*0*0*0*0	12466.59
0	0	0	7*5*4*0*0*0-0*0*0*0*0*0	12466.59
0	0	0	7*5*4*0*0*0-0*0*0*0*0*0	12466.59
1	1	0	6*5*4*4*0*0-0*0*0*0*0*0	16364.77	d	0	0	1	1	1	1	a		4	1	1		6		0	0	6	6	6	6		130
1	0	1	6*5*4*4*0*0-0*0*0*0*0*0	16364.77
1	0	0	6*5*4*4*0*0-0*0*0*0*0*0	16364.77
1	0	0	6*5*4*4*0*0-0*0*0*0*0*0	16364.77
0	0	0	6*5*4*4*0*0-0*0*0*0*0*0	16364.77
0	0	0	6*5*4*4*0*0-0*0*0*0*0*0	16364.77
0	0	1	1*6*1*1*1*0-0*0*0*0*0*0	20399.01	d	0	1	1	1	1	1	a		4	1	1		6		0	6	6	6	6	6		181.25
1	1	0	1*6*1*1*1*0-0*0*0*0*0*0	20399.01
0	0	1	1*6*1*1*1*0-0*0*0*0*0*0	20399.01
0	0	1	1*6*1*1*1*0-0*0*0*0*0*0	20399.01
0	0	1	1*6*1*1*1*0-0*0*0*0*0*0	20399.01
0	0	0	1*6*1*1*1*0-0*0*0*0*0*0	20399.01
1	1	0	6*3*6*0*0*0-0*0*0*0*0*0	26558.57	d	0	0	0	1	1	1	a		3	2	1		8.75		0	0	0	8.75	8.75	8.75		172.2656
0	1	1	6*3*6*0*0*0-0*0*0*0*0*0	26558.57
1	1	0	6*3*6*0*0*0-0*0*0*0*0*0	26558.57
0	0	0	6*3*6*0*0*0-0*0*0*0*0*0	26558.57
0	0	0	6*3*6*0*0*0-0*0*0*0*0*0	26558.57
0	0	0	6*3*6*0*0*0-0*0*0*0*0*0	26558.57
1	1	0	6*6*6*0*0*0-0*0*0*0*0*0	29212.8	d	0	0	0	1	1	1	a		3	3	0		9		0	0	0	9	9	9		182.25
1	1	0	6*6*6*0*0*0-0*0*0*0*0*0	29212.8
1	1	0	6*6*6*0*0*0-0*0*0*0*0*0	29212.8
0	0	0	6*6*6*0*0*0-0*0*0*0*0*0	29212.8
0	0	0	6*6*6*0*0*0-0*0*0*0*0*0	29212.8
0	0	0	6*6*6*0*0*0-0*0*0*0*0*0	29212.8
1	0	1	5*6*3*0*0*0-0*0*0*0*0*0	35119.03	d	0	0	0	1	1	1	a		2	2	2		9		0	0	0	9	9	9		182.25
1	1	0	5*6*3*0*0*0-0*0*0*0*0*0	35119.03
0	1	1	5*6*3*0*0*0-0*0*0*0*0*0	35119.03
0	0	0	5*6*3*0*0*0-0*0*0*0*0*0	35119.03
0	0	0	5*6*3*0*0*0-0*0*0*0*0*0	35119.03
0	0	0	5*6*3*0*0*0-0*0*0*0*0*0	35119.03
1	1	1	7*7*0*0*0*0-0*0*0*0*0*0	41786.45	d	0	0	0	0	1	1	a		2	2	2		9		0	0	0	0	9	9		81
1	1	1	7*7*0*0*0*0-0*0*0*0*0*0	41786.45
0	0	0	7*7*0*0*0*0-0*0*0*0*0*0	41786.45
0	0	0	7*7*0*0*0*0-0*0*0*0*0*0	41786.45
0	0	0	7*7*0*0*0*0-0*0*0*0*0*0	41786.45
0	0	0	7*7*0*0*0*0-0*0*0*0*0*0	41786.45

收敛误差7e-4，每组收敛199次。统计平均值。

首先统计差值结构的行分布与列分布，由列分布计算行排斥力，行排斥力的结果作为平均列的列系数，计算平均列的列斥力。

如计算第一个

差值结构			A-B	迭代次数
1	1	1	7*1*4*2*0*0-0*0*0*0*0*0	3106.407
0	0	1	7*1*4*2*0*0-0*0*0*0*0*0	3106.407
1	0	0	7*1*4*2*0*0-0*0*0*0*0*0	3106.407
0	1	0	7*1*4*2*0*0-0*0*0*0*0*0	3106.407
0	0	0	7*1*4*2*0*0-0*0*0*0*0*0	3106.407
0	0	0	7*1*4*2*0*0-0*0*0*0*0*0	3106.407

列分布是2，2，2计算行排斥力

	2	2	2
2		4	1
2			4
2

F=9

行分布在紧密堆积的条件下是0，0，1，1，1，3，但因为列排斥力与数量无关，因此等价于0，0，1，1，1，1.

因为列系数=行排斥力=9因此平均列为

0，0，9，9，9，9，用同样的办法计算列排斥力

	0	0	9	9	9	9
0				81	20.3	9
0					81	20.3
9						81
9
9
9

F=292.5

计算其余各组得到

迭代次数	列排斥力
3106.407	292.5
3367.935	407.8125
3476.296	322.222222
4038.91	407.8125
4086.126	276.475694
5254.709	292.5
6307.814	182.25
9720.759	181.25
11051.61	130
12238.71	231.111111
12367.27	125.868056
12466.59	172.265625
16364.77	130
20399.01	181.25
26558.57	172.265625
29212.8	182.25
35119.03	182.25
41786.45	81

列排斥力与迭代次数大体上成反比关系，因为这里任一个行分布与列分布组合对应的差值结构都是唯一的，因此任意两个组合之间的变化都与路径无关，有势能的特征，因此这里的迭代次数与势能成反比，势能越低结构越稳定，拆开的难度越大，迭代次数越大。