伺服电机堵转检测

一. 电流数据的分析

电机工作时的电流如下图：

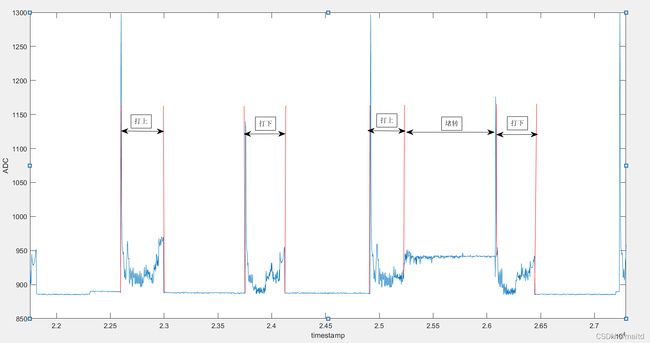
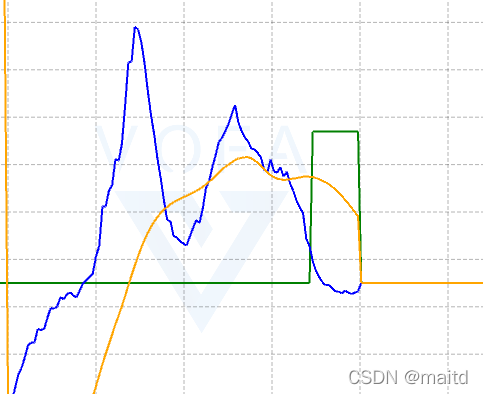
电机正常工作时，电机电流具有两个状态：正常旋转和堵转。
正常旋转时，电流在控制算法的作用下，一开始会有很快的上升，过程中电流受到控制算法的作用，没有平稳阶段。
堵转时，电机结束了控制算法，所以堵转时电流上升然后保持一段时间的平稳状态。
用电流曲线的斜率描述这一状态：开始斜率是正的，然后斜率变为0。所以可以计算电流曲线的斜率来识别电机是否处于堵转状态。

二. 检测原理

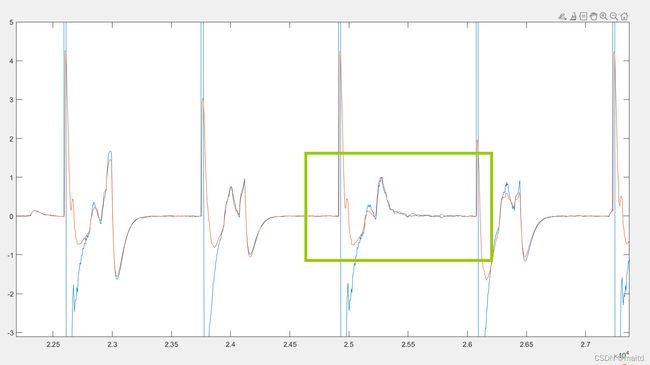
上图中黄色曲线为matlab计算得出的电流曲线斜率，蓝色曲线为单片机计算得出的斜率。
实际上由于所使用的算法在长时间运行下存在过拟合，所以在实际中，在电机开始工作时对算法的参数做重新的初始化，导致单片机一开始的计算结果波动较大。
算法的基本流程：

1.检测斜率是否接近于0，如果接近于0说明电流此时处于平稳的状态。
2.检测此时斜率的均值，均值是此时刻及之前40个时刻的斜率值得均值。若此时刻均值大于0.3说明，在过去的40个时刻电流是上升状态。
3.若此刻斜率均值大于0.3，检测此时刻后300ms内斜率是否会小于-0.2。若存在这种情况说明电流又快速下降，手指并未处在堵转状态。
4.没有小于-0.2的情况，说明电机此时处于堵转状态。

三. 斜率计算实现

考虑到单片机的性能限制，使用了递推最小二乘方法来递推电流曲线的斜率，并使用队列来保存40个时刻的斜率数据用来递推均值，减少运算量。为了能尽快的使计算结果跟踪电流曲线的变化，在开始的40个计算周期内使用带遗忘因子的递推最小二乘，之后使用有限数据窗+遗忘因子的方式计算。数据窗的长度即参与计算的数据个数为40个。
算法原理可参考以下博客
https://blog.csdn.net/qq_33243369/article/details/102713303

四. 实际效果

可以在发生过流后70ms左右检测到过流。

图中蓝色曲线是计算得出的电流斜率。黄色曲线为电流斜率的递推均值，绿色曲线代表有无检测出过流。

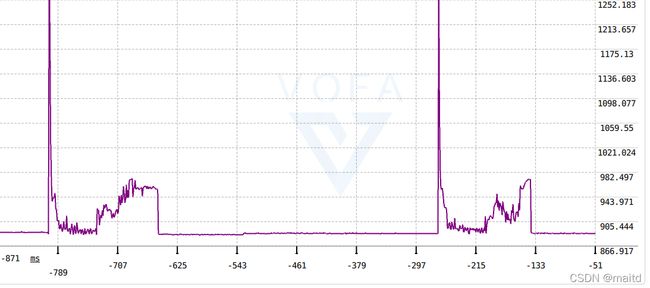
在检测出过流后，将手指电机占空比设置为0.上图第二段曲线是手指正常打下的电流曲线，第一段曲线是手指打下后有堵转，可以看到堵转后70ms内电流回复了正常值。

五.代码实现

least_squares.h

#ifndef _LEAST_SQUARES_H
#define _LEAST_SQUARES_H



#include "queue.h"

typedef struct
{
    float   P[4];
	  float   L[2];
	  float   Q[4];
	  float   lam_p;
	  float   lamp;
      QUEUE   K0_q;
	  QUEUE   K1_q;
	  float   K[2];
      float   lam;
      QUEUE   cur;
	  float   last_mean_cur;
	 // unsigned int  i;
	  uint32_t phi;
	  float mean_k;
	  float k_sum;
	  float start_time;
	  float check_f;
	  uint8_t overcur;
	  float cur_sum;
	  float mean_cur;
} least_squares_paras_t;


void least_squares_init(void);
void least_squares_porcess(float cur);
#endif

least_squares.c

#include "least_squares.h"
#include "math.h"
least_squares_paras_t least_squares_paras;
extern robot_finger_module_t robot_finger_module;


//init paras
void least_squares_init(void)
{
	least_squares_paras.lam = 0.9;
	least_squares_paras.lam_p = 67.6550;
	least_squares_paras.lamp = 0.0148;
    least_squares_paras.phi = 1;
	least_squares_paras.k_sum=0;
	least_squares_paras.mean_k=0;
	least_squares_paras.P[0] = 1000000;
	least_squares_paras.P[1] = 0;
	least_squares_paras.P[2] = 0;
	least_squares_paras.P[3] = 1000000;
	least_squares_paras.K[0] = 0;
	least_squares_paras.K[1] = 0;
	least_squares_paras.check_f = 0;
	least_squares_paras.overcur=0;
	CreateQueue(&least_squares_paras.cur,40);
	CreateQueue(&least_squares_paras.K0_q,40);
	CreateQueue(&least_squares_paras.K1_q,40);
}



void least_squares_porcess(float cur)
{

	//time counter
  least_squares_paras.phi++;
	
	//queue is not full, use forgetting factor
	if(!FullQueue(&least_squares_paras.cur))
	{
		Enqueue(&least_squares_paras.cur,cur);
		least_squares_paras.cur_sum+=cur;
		least_squares_paras.mean_cur = least_squares_paras.cur_sum/least_squares_paras.cur.rear;
		
		//Extract the reused process value and calculate it separately
		float res1 = least_squares_paras.lam + least_squares_paras.phi*least_squares_paras.phi*least_squares_paras.P[0]
		           + least_squares_paras.phi*least_squares_paras.P[1]
	               + least_squares_paras.phi*least_squares_paras.P[2]
	               + least_squares_paras.P[3];
	
	  //calculate L
		least_squares_paras.L[0] = (least_squares_paras.P[0]*least_squares_paras.phi+least_squares_paras.P[1])/res1;
		least_squares_paras.L[1] = (least_squares_paras.P[2]*least_squares_paras.phi+least_squares_paras.P[3])/res1;

    //calculate P
		float P_t[4] = {least_squares_paras.P[0],least_squares_paras.P[1],least_squares_paras.P[2],least_squares_paras.P[3]};
		least_squares_paras.P[0] = (P_t[0]*(1-least_squares_paras.L[0]*least_squares_paras.phi)
															 - least_squares_paras.L[0]*P_t[2])/least_squares_paras.lam;

		least_squares_paras.P[1] = (P_t[1]*(1-least_squares_paras.L[0]*least_squares_paras.phi)
															 - least_squares_paras.L[0]*P_t[3])/least_squares_paras.lam;

		least_squares_paras.P[2] = (P_t[2]*(1-least_squares_paras.L[1])
															 - least_squares_paras.L[1]*P_t[0]*least_squares_paras.phi)/least_squares_paras.lam;

		least_squares_paras.P[3] = (P_t[3]*(1-least_squares_paras.L[1])
															 - least_squares_paras.L[1]*P_t[1]*least_squares_paras.phi)/least_squares_paras.lam;
		
		//calculate slope
		float K_o[2]={least_squares_paras.K[0] ,least_squares_paras.K[1]};
    least_squares_paras.K[0] = least_squares_paras.K[0] 
	                           + least_squares_paras.L[0]*(cur - least_squares_paras.phi*K_o[0]-K_o[1]);
	  least_squares_paras.K[1] = least_squares_paras.K[1] 
                            + least_squares_paras.L[1]*(cur - least_squares_paras.phi*K_o[0]-K_o[1]);
		
		Enqueue(&least_squares_paras.K0_q,least_squares_paras.K[0]);
		Enqueue(&least_squares_paras.K1_q,least_squares_paras.K[1]);
		least_squares_paras.k_sum+=least_squares_paras.K[0];
		least_squares_paras.mean_k = least_squares_paras.k_sum/least_squares_paras.K0_q.rear;
		
		
	}
	else //queue is full,use Limited data window and forgetting factor
	{
		//current before 40 cycles
		float cur_p =0;
		
		//the present time
    float t = least_squares_paras.phi;
	  
		//time before 40 cycles
		float t_p = least_squares_paras.phi-40;
		
		//Extract the reused process value and calculate it separately
		Dequeue(&least_squares_paras.cur,&cur_p);
		float p_t[10];
		uint8_t p_cnt = 0;
		for(int i=0;i<4;i++)
		{
			for(int j=i;j<4;j++)
			{
				p_t[p_cnt]=least_squares_paras.P[i]*least_squares_paras.P[j];
				p_cnt++;
			}
		}
		
		float res = least_squares_paras.lam+least_squares_paras.P[3]
								+t*(least_squares_paras.P[2]+t*least_squares_paras.P[0]+least_squares_paras.P[1]);


    //calculate Q
		least_squares_paras.Q[0] = (least_squares_paras.P[0]-(p_t[5]+t*p_t[2]+t*p_t[1]+t*t*p_t[0])/res)/least_squares_paras.lam;
		least_squares_paras.Q[1] = (least_squares_paras.P[1]-(p_t[6]+t*p_t[3]+t*p_t[4]+t*t*p_t[1])/res)/least_squares_paras.lam;
		least_squares_paras.Q[2] = (least_squares_paras.P[2]-(p_t[8]+t*p_t[7]+t*p_t[3]+t*t*p_t[2])/res)/least_squares_paras.lam;
		least_squares_paras.Q[3] = (least_squares_paras.P[3]-(p_t[9]+t*p_t[8]+t*p_t[6]+t*t*p_t[5])/res)/least_squares_paras.lam;

		
		//Extract the reused process value and calculate it separately
		float q_t[10];
		uint8_t q_cnt = 0;
		for(int i=0;i<4;i++)
		{
			for(int j=i;j<4;j++)
			{
				q_t[q_cnt]=least_squares_paras.Q[i]*least_squares_paras.Q[j];
				q_cnt++;
			}
		}

		
		res = least_squares_paras.Q[3]-least_squares_paras.lam_p+t_p*(least_squares_paras.Q[2]+t_p*least_squares_paras.Q[0]+least_squares_paras.Q[1]);

		//calculate Q
		least_squares_paras.P[0] = least_squares_paras.Q[0]-(q_t[5]+t_p*q_t[2]+t_p*q_t[1]+t_p*t_p*q_t[0])/res;
		least_squares_paras.P[1] = least_squares_paras.Q[1]-(q_t[6]+t_p*q_t[3]+t_p*q_t[4]+t_p*t_p*q_t[1])/res;
		least_squares_paras.P[2] = least_squares_paras.Q[2]-(q_t[8]+t_p*q_t[7]+t_p*q_t[3]+t_p*t_p*q_t[2])/res;
		least_squares_paras.P[3] = least_squares_paras.Q[3]-(q_t[9]+t_p*q_t[8]+t_p*q_t[6]+t_p*t_p*q_t[5])/res;
		

		//calculate slope
		float K_o[2]={least_squares_paras.K[0] ,least_squares_paras.K[1]};
		float res1 = K_o[1]-cur+t*K_o[0];
		float res2 = K_o[1]-cur_p+t_p*K_o[0];
		least_squares_paras.K[0] = K_o[0]-(least_squares_paras.P[1]+t*least_squares_paras.P[0])*res1
		         +(least_squares_paras.lamp*least_squares_paras.P[1]+least_squares_paras.lamp*least_squares_paras.P[0]*t_p)*res2;
		
		least_squares_paras.K[1] = K_o[1]-(least_squares_paras.P[3]+t*least_squares_paras.P[2])*res1
		         +(least_squares_paras.lamp*least_squares_paras.P[3]+least_squares_paras.lamp*least_squares_paras.P[2]*t_p)*res2;
		
		float K_p[2];
		Dequeue(&least_squares_paras.K0_q,&K_p[0]);
		Dequeue(&least_squares_paras.K1_q,&K_p[1]);
		least_squares_paras.k_sum=least_squares_paras.k_sum-K_p[0]+least_squares_paras.K[0];
		least_squares_paras.mean_k = least_squares_paras.k_sum/least_squares_paras.K0_q.maxsize;
		Enqueue(&least_squares_paras.K0_q,least_squares_paras.K[0]);
		Enqueue(&least_squares_paras.K1_q,least_squares_paras.K[1]);
	  Enqueue(&least_squares_paras.cur,cur);
	}
	
	

	
	if(least_squares_paras.check_f)
	{
		uint32_t time = HAL_GetTick();
		
		if(time>least_squares_paras.start_time+150&&time<least_squares_paras.start_time+450)
		{
			if(least_squares_paras.K[0]>0&&least_squares_paras.K[0]<0.2&&least_squares_paras.mean_k>0.35)
			{
				least_squares_paras.overcur=1;
			}
			if(least_squares_paras.K[0]<-0.2)
			{
				least_squares_paras.overcur=0;
			}
		}
		else if(time>least_squares_paras.start_time+450&&time<least_squares_paras.start_time+800)
		{
			//least_squares_paras.check_f=0;
			ClearQuene(&least_squares_paras.cur);
			ClearQuene(&least_squares_paras.K0_q);
			ClearQuene(&least_squares_paras.K1_q);
			least_squares_paras.phi = 1;
			least_squares_paras.k_sum=0;
			least_squares_paras.mean_k=0;
			least_squares_paras.P[0] = 100;
			least_squares_paras.P[1] = 0;
			least_squares_paras.P[2] = 0;
			least_squares_paras.P[3] = 100;
			least_squares_paras.K[0] = 0;
			least_squares_paras.K[1] = 0;
			
			
			least_squares_paras.mean_k = 0;
			
			if(least_squares_paras.overcur)
			{
				//检测出过流，执行相应的保护操作				
			}
			least_squares_paras.overcur=0;
		}
		else if(time>least_squares_paras.start_time+800)
		{
			least_squares_paras.check_f=0;
		}
	}
		
}

queue.h

#ifndef __QUEUE_H_
#define __QUEUE_H_
typedef struct queue 
{
	float *pBase;
	int front;    
	int rear;   
	int maxsize; 
}QUEUE,*PQUEUE;
 
void ClearQuene(PQUEUE Q);
void CreateQueue(PQUEUE Q,int maxsize);
void TraverseQueue(PQUEUE Q);
int FullQueue(PQUEUE Q);
int EmptyQueue(PQUEUE Q);
int Enqueue(PQUEUE Q, float val);
int Dequeue(PQUEUE Q, float *val);
#endif

queue.c

#include
#include"queue.h"
/***********************************************
Function: Create a empty stack;
************************************************/
void CreateQueue(PQUEUE Q,int maxsize)
{
	Q->pBase=(float *)malloc(sizeof(float)*maxsize);
	if(NULL==Q->pBase)
	{
		return;
	}
	Q->front=0;         
	Q->rear=0;
	Q->maxsize=maxsize;
}

void ClearQuene(PQUEUE Q)
{
	Q->front=0;         
	Q->rear=0;
}
/***********************************************
Function: Print the stack element;
************************************************/
void TraverseQueue(PQUEUE Q)
{
	int i=Q->front;

	while(i%Q->maxsize!=Q->rear)
	{
		//printf("%d ",Q->pBase[i]);
		i++;
	}
	//printf("\n");
}
int FullQueue(PQUEUE Q)
{
	if(Q->front==(Q->rear+1)%Q->maxsize)    
		return 1;
	else
		return 0;
}
int EmptyQueue(PQUEUE Q)
{
	if(Q->front==Q->rear)    
		return 1;
	else
		return 0;
}
int Enqueue(PQUEUE Q, float val)
{
	if(FullQueue(Q))
		return 0;
	else
	{
		Q->pBase[Q->rear]=val;
		Q->rear=(Q->rear+1)%Q->maxsize;
		return 1;
	}
}


int Dequeue(PQUEUE Q, float *val)
{
	if(EmptyQueue(Q))
	{
		return 0;
	}
	else
	{
		*val=Q->pBase[Q->front];
		Q->front=(Q->front+1)%Q->maxsize;
		return 1;
	}
}