linux ida和idr分配机制
在看v4l2架构的媒体设备注册media_device_register_entity时发现调用ida_get_new_above分配id,虽然对继续阅读和理解整体代码完全没有影响,由于求知欲和好奇心的驱使下还是决定看看,然而还是没看懂,直线救国,直接到网上看了几篇博客,虽然与我看的源码实现不同,但还是花了不少时间学习一下,保证对继ida和idr也有个从0到1的认识,继续看源码也有个基础。学习linux内核源码没有什么捷径,就是这样慢慢积累。
本文先介绍一下ida和idr的原理和实现的过程,后面再进行详细的源码分析,如果只是想了解大致的实现过程,阅读ida和idr原理这部分就足够了。
ida和idr原理
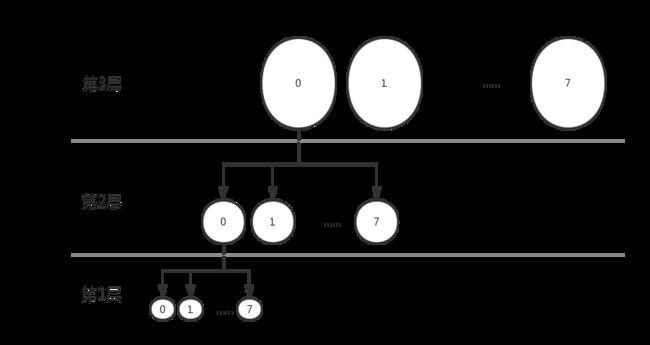
ida和idr用于对内核中的整数资源的分配和管理的机制,可以为内核中的其他功能模块提供一种获取并占用唯一整数id的方法。idr机制中,采用了类似于基数树的数据结构进行管理,树的结构被分为从上到下的多个层,每一层中的节点管理着整数id中对应的多个连续位表示的数值对应的分支,这些分支形成的子节点就是新的一层中的节点。根节点的一层是必须的,如果树还没有建立,则第一层为空。
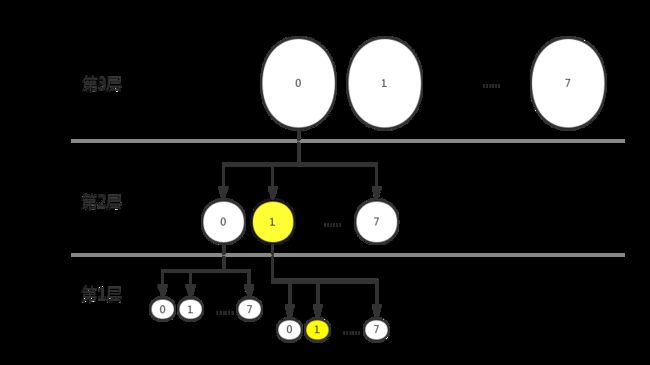
最后一层的叶节点的bitmap位图中的一个位对应一个整数id,用于表示该id是否已经被申请使用,1表示使用,0表示空闲。普通层的节点bitmap位图中的每一位对应一个下一层的子节点,用于表示子节点为根的子树管理的所有整数id是否已经被全部申请使用,1表示使用,0表示空闲,存在空闲节点槽位。查找一个整数是否已经被使用时的查找路径,就是从根节点出发经过整数id对一应的中间层节点到最后一层的叶节点的路径(不考虑中间层某个节点的子树管理的id已经被全部申请,这样不用查找到最后一层)。这个路径代表着一个被管理的完整的整数id(如下图中的黄色节点的路径,表示id=011),叶节点中的bitmap位图直接标志着整数id是否被申请使用的情况,所以也可以理解为叶节点是最终的整数id资源的直接管理者。
申请整数id的过程:
1、判断当前树管理的最大整数是否大于要申请的id,如果大于,则进行第2步骤,否则(这种情况说明树的规模还不足以申请id,需要增加树的层级以扩大管理的整数范围)建立新节点作为根节点,将旧的根节点作为新的根节点的第一个子节点,再跳转到第1步骤继续判断。
2、前面步骤1中已经完成满足id申请要求的树的层数构建,这一步需要根据整数id,从根节点查找id对应的每一层中对应的节点,如果节点为空,说明这个节点之前未被建立,则为其建立新节点,继续下一层查找;如果节点已经建立但未被使用,则继续下一层查找直到叶节点为止;如果节点已经被使用,则查找同一层的下个相邻兄弟节点,如果兄弟节点未被使用,继续向弟节点的子节点查找,否则返回父节点,对下一个兄弟节点继续查找。
3、最终查找到叶节点后,判断id对应的叶节点的bitmap位图的位是否置位(为1),如果置位,说明该id已经被使用,返回失败;如果未被置位,将其置位,返回成功,完成id申请。
通过树这种方式进行管理,最后还是通过树的叶节点中的位来标志对应的整数是否被使用,那么为什么不直接用一个数组并将其中的位用来表示对应整数来实现整数管理,而且能够直接索引到整数位置,这样岂不是更简单更高效?
问题的关键在于数组是连续存储空间,而整数管理机制需要管理不连续的整数id,特别是当两个被申请占用的整数之间跨度比较大时对空间的浪费就比较明显。此外,使用数组是一种静态的管理方式,不能根据实际情况申请和释放占用的资源而降低空间的利用率。如果使用这种树管理,则会根据申请的整数的大小,对当前的树的大小进行调整,虽然也存在一定的稀疏性问题而且看似还使用更多的额外空间去构建树,但它能够将稀疏程度控制在一个叶节点上,也就是说,申请一个整数,最多占用一个叶节点的空间(具体还包括叶节点到根所构建的路径占用的空间),假设一个叶节点能够管理8个整数,即使只管理一个,也有1/8的利用率(最低就是1/8,因为0的话就不会生成该叶节点)。对于构建树需要的额外空间,当管理整数的范围比较大时且稀疏程度也比较大的整数时,这些额外空间就远小于稀疏数组所浪费的空间。另外,树在保持对稀疏整数的空间管理上的优势之外,在查找效率方面并不会比数组直接索引慢很多,可以通过增加每一层管理的整数数量,降低树的高度,提升查找和调整树的效率(申请的id能够直接确定了每一层的查找位置,效率与层数相关;有些时候需要考虑申请时遍历节点位图查找空闲槽点的操作,所以复杂度为mlogm(n) ,m为一个节点的子节点数,n为管理的id的最大值),同时,空间复杂度也会降低(在满树的情况下,当树的叶节点相同时,层数越小,总的节点数越小,树的空间复杂度与总节点数成正比(包括随着每一层节点的子节点数变化的位图和记录下一子节点的数组占用空间也是如此)) ,当层数只有一层的时退化为数组,查找效率最高,同时也是最省空间,但此时叶节点利用率最低,而采用树的数据结构能够提高对稀疏整数管理的灵活度而节省未被使用的空间。
源码实现
开始阅读代码前可以先根据原理思考大概需要什么样的数据结构才合理实现树的操作(目的是锻炼在面对未知领域或者拆解黑箱时,能够利用最少的信息,掌握或推理最多的整体合理有效信息,快速拓展对未知部分的理解),大概要通过这些数据结构怎么实现(基本思考方向是用最少的空间实现高效的性能),形成自己对问题的整体思考框架,再通过实际代码去检验和修正。
/*
ida封装idr,idr管理一棵树,free_bitmap用于申请时没有空闲位图使用
*/
struct ida {
struct idr idr;
struct ida_bitmap *free_bitmap;
};
struct ida_bitmap {
long nr_busy;
unsigned long bitmap[IDA_BITMAP_LONGS];
};
/*
idr表示一整颗树,包含一棵树的全部信息,hint是树中最后申请到的idr_layer,top是树
的根部,从这里开始能够遍历整棵树的数据。
id_free存储空闲的结构体,构建新的层可以用到
*/
struct idr {
struct idr_layer __rcu *hint; /* the last layer allocated from */
struct idr_layer __rcu *top;
int layers; /* only valid w/o concurrent changes */
int cur; /* current pos for cyclic allocation */
spinlock_t lock;
int id_free_cnt;
struct idr_layer *id_free;
};
struct idr_layer {
int prefix; /* the ID prefix of this idr_layer */
int layer; /* distance from leaf */
struct idr_layer __rcu *ary[1<idr, gfp_mask))
return 0;
/* allocate free_bitmap */
if (!ida->free_bitmap) {
struct ida_bitmap *bitmap;
bitmap = kmalloc(sizeof(struct ida_bitmap), gfp_mask);
if (!bitmap)
return 0;
free_bitmap(ida, bitmap);
}
return 1;
}
static int __idr_pre_get(struct idr *idp, gfp_t gfp_mask)
{
//连续申请空闲idr_layer,挂在到idp->id_free链表中,直到空闲idr_layer的个数满足要求
while (idp->id_free_cnt < MAX_IDR_FREE) {
struct idr_layer *new;
new = kmem_cache_zalloc(idr_layer_cache, gfp_mask);
if (new == NULL)
return (0);
move_to_free_list(idp, new);
}
return 1;
}
static void move_to_free_list(struct idr *idp, struct idr_layer *p)
{
unsigned long flags;
/*
* Depends on the return element being zeroed.
*/
spin_lock_irqsave(&idp->lock, flags);
__move_to_free_list(idp, p);
spin_unlock_irqrestore(&idp->lock, flags);
}
static void __move_to_free_list(struct idr *idp, struct idr_layer *p)
{
//将空闲的idr_layer挂载在idp->id_free起始的链表中
p->ary[0] = idp- >id_free;
idp->id_free = p;
idp->id_free_cnt++;
}
static void free_bitmap(struct ida *ida, struct ida_bitmap *bitmap)
{
unsigned long flags;
if (!ida->free_bitmap) {
spin_lock_irqsave(&ida->idr.lock, flags);
if (!ida->free_bitmap) {
ida->free_bitmap = bitmap;
bitmap = NULL;
}
spin_unlock_irqrestore(&ida->idr.lock, flags);
}
kfree(bitmap);
}
/*
先看整体,大概猜想整体功能怎么实现的,不懂的地方可以结合上下文逻辑、定义、计算、
变量作为函数的什么参数调用等理解;再看调用函数实现的细节
*/
int ida_get_new_above(struct ida *ida, int starting_id, int *p_id)
{
struct idr_layer *pa[MAX_IDR_LEVEL + 1];
struct ida_bitmap *bitmap;
unsigned long flags;
//计算申请的起始id在第idr_id个IDA_BITMAP_BITS中的第offset位
int idr_id = starting_id / IDA_BITMAP_BITS;
int offset = starting_id % IDA_BITMAP_BITS;
int t, id;
restart:
/* get vacant slot */
//在树ida->idr中获取空槽
t = idr_get_empty_slot(&ida->idr, idr_id, pa, 0, &ida->idr);
if (t < 0)
return t == -ENOMEM ? -EAGAIN : t;
//大于树能够管理的最大数量
if (t * IDA_BITMAP_BITS >= MAX_IDR_BIT)
return -ENOSPC;
//实际申请的id与起始申请starting_id不一致,说明被占用了,从starting_id后找一个有空槽的
if (t != idr_id)
offset = 0;
idr_id = t;
/* if bitmap isn't there, create a new one */
/*
根据定义中MAX_IDR_LEVEL,可知这里pa存放不同层的idr_layer,既从根部到叶节点的路径
idr_id中每连续的三位表示每一层中的索引,即本idr_id表示的整数在某层的第几个分支,
依次查找每一层,直到叶节点最后一层是叶节点的ary成员是ida_bitmap而不是idr_layer
*/
bitmap = (void *)pa[0]->ary[idr_id & IDR_MASK];
//申请到的节点的位图为空,说明之前没有被申请过
if (!bitmap) {
spin_lock_irqsave(&ida->idr.lock, flags);
bitmap = ida->free_bitmap;
ida->free_bitmap = NULL;
spin_unlock_irqrestore(&ida->idr.lock, flags);
if (!bitmap)
return -EAGAIN;
memset(bitmap, 0, sizeof(struct ida_bitmap));
rcu_assign_pointer(pa[0]->ary[idr_id & IDR_MASK],
(void *)bitmap);
pa[0]->count++;
}
/* lookup for empty slot */
t = find_next_zero_bit(bitmap->bitmap, IDA_BITMAP_BITS, offset);//从bitmap->bitmap的offset位之后查找第一个非零位的位置,这些bitmap中的位表示对应的整数是否空闲
if (t == IDA_BITMAP_BITS) {
/* no empty slot after offset, continue to the next chunk */
idr_id++;
offset = 0;
goto restart;
}
id = idr_id * IDA_BITMAP_BITS + t;
if (id >= MAX_IDR_BIT)
return -ENOSPC;
__set_bit(t, bitmap->bitmap);
if (++bitmap->nr_busy == IDA_BITMAP_BITS)//节点中的槽位都被使用,则节点在父节点中的槽位会被置一,这个在sub_alloc()函数中要注意
idr_mark_full(pa, idr_id);
*p_id = id;
/* Each leaf node can handle nearly a thousand slots and the
* whole idea of ida is to have small memory foot print.
* Throw away extra resources one by one after each successful
* allocation.
*/
/*
释放从move_to_free_list()申请的剩余空闲idr_layer
*/
if (ida->idr.id_free_cnt || ida->free_bitmap) {
struct idr_layer *p = get_from_free_list(&ida->idr);
if (p)
kmem_cache_free(idr_layer_cache, p);
}
return 0;
}
static int idr_get_empty_slot(struct idr *idp, int starting_id,
struct idr_layer **pa, gfp_t gfp_mask,
struct idr *layer_idr)
{
struct idr_layer *p, *new;
int layers, v, id;
unsigned long flags;
id = starting_id;
build_up:
p = idp->top;
layers = idp->layers;//树的总层数
if (unlikely(!p)) {
if (!(p = idr_layer_alloc(gfp_mask, layer_idr)))
return -ENOMEM;
p->layer = 0;//只有一层,树根也是叶节点
layers = 1;//总层数
}
/*
* Add a new layer to the top of the tree if the requested
* id is larger than the currently allocated space.
*/
/*
这个循环的目的是添加新的层到树的top(根)层,直到构建一颗能够管理大于id这个整数的树
*/
while (id > idr_max(layers)) {
layers++;
if (!p->count) {
/* special case: if the tree is currently empty,
* then we grow the tree by moving the top node
* upwards.
*/
/*
结合本函数和下面的函数sub_alloc()中对p->count这个成员的使用,
可知该成员为节点存在的子节点的计数。
空树时直接提升层数,不用新建树根等操作,构建子树的空节点在之后的sub_alloc()函数中进行
如果树存在子树,那么在下面的程序中,将子树插入到新建的根中
*/
p->layer++;
WARN_ON_ONCE(p->prefix);
continue;
}
if (!(new = idr_layer_alloc(gfp_mask, layer_idr))) {
/*
* The allocation failed. If we built part of
* the structure tear it down.
*/
/*
构建树的过程中,如果存在失败的情况,释放前面所有构造的节点层
*/
spin_lock_irqsave(&idp->lock, flags);
for (new = p; p && p != idp->top; new = p) {
p = p->ary[0];
new->ary[0] = NULL;
new->count = 0;
bitmap_clear(new->bitmap, 0, IDR_SIZE);
__move_to_free_list(idp, new);
}
spin_unlock_irqrestore(&idp->lock, flags);
return -ENOMEM;
}
/*
构造树时,树是向上,向树根方向生长的。这里构造新的树根,并将旧树放置在其下,
旧树表示的整数为新树的最小部分,所以旧树的树根被放置在新树根的第一个空槽中
*/
new->ary[0] = p;
new->count = 1;
new->layer = layers-1;
new->prefix = id & idr_layer_prefix_mask(new->layer);//计算当前层对应id中的几个连续的位中的数值
/*
为空,说明p为根的子树中的id全部没有被使用过,对应到其父节点中的bitmap中的位清零。
需要注意,bitmap为空时,树不一定为空,bitmap表示以该节点为根的子树的id被使用的情况
*/
if (bitmap_full(p->bitmap, IDR_SIZE))
__set_bit(0, new->bitmap);
p = new;
}
rcu_assign_pointer(idp->top, p);//把p赋值给idp->top,作为新的树根
idp->layers = layers;
v = sub_alloc(idp, &id, pa, gfp_mask, layer_idr); //开始根据id查找和构造子节点,id使用指针说明传入的id和实际申请的可能不同,所以需要输出
if (v == -EAGAIN)
goto build_up;
return(v);
}
static int sub_alloc(struct idr *idp, int *starting_id, struct idr_layer **pa,
gfp_t gfp_mask, struct idr *layer_idr)
{
int n, m, sh;
struct idr_layer *p, *new;
int l, id, oid;
id = *starting_id;
restart:
p = idp->top;
l = idp->layers;
pa[l--] = NULL;//总共有idp->layers层,pa用来存放最终查找到的整数时,查找的路径上经过的每一层的节点的地址。
//l的循环为idp->layers-1到 1
while (1) {
/*
* We run around this while until we reach the leaf node...
*/
n = (id >> (IDR_BITS*l)) & IDR_MASK;//第l层对应的id中连续IDR_BITS位的数值
m = find_next_zero_bit(p->bitmap, IDR_SIZE, n);//查找p->bitmap中大于等于n之后的第一个0的位的位置,即查找空闲位的槽的位置
//可以先跳过这些条件,理清后面思路,有个整体思路后再回来补充这些条件作了什么操作
/*
结合修改p->bitmap的地方分析代码(即前面idr_get_empty_slot()和ida_get_new_above()中对bitmap的置位以及调用bitmap_full()的地方),
如果子树管理的id全部已经被申请,则子树的根节点对应的bitmap的位会被置一。
m == IDR_SIZE时p->bitmap中没有大于等于n的空闲槽位,此时p节点管理的子树对应的整数可能并未全部被使用
*/
if (m == IDR_SIZE) {
/* no space available go back to previous layer. */
l++;
oid = id;
id = (id | ((1 << (IDR_BITS * l)) - 1)) + 1;//比当前l层对应的id部分的连续位加一,效果就是在下次到while时,给n加一,换个大一级的槽位
/* if already at the top layer, we need to grow */
if (id > idr_max(idp->layers)) {
*starting_id = id;
return -EAGAIN;
}
p = pa[l];//返回上一层
BUG_ON(!p);
/* If we need to go up one layer, continue the
* loop; otherwise, restart from the top.
*/
sh = IDR_BITS * (l + 1);
if (oid >> sh == id >> sh)
continue;
else
goto restart;//id | ((1 << (IDR_BITS * l)) - 1)) + 1 溢出
}
if (m != n) {
sh = IDR_BITS*l;
id = ((id >> sh) ^ n ^ m) << sh;
}
if ((id >= MAX_IDR_BIT) || (id < 0))
return -ENOSPC;
if (l == 0)
break;
/*
* Create the layer below if it is missing.
*/
if (!p->ary[m]) {
new = idr_layer_alloc(gfp_mask, layer_idr);
if (!new)
return -ENOMEM;
new->layer = l-1;
new->prefix = id & idr_layer_prefix_mask(new->layer);
rcu_assign_pointer(p->ary[m], new);
p->count++;
}
pa[l--] = p;// pa[l]对应l + 1层的layers,在该层中,(id >> (IDR_BITS*l)) & IDR_MASK为id对应的子节点在p->ary中的位置
p = p->ary[m];
}
//l == 0,该层p的子节点的位置为id & IDR_MASK,与函数ida_get_new_above()中的使用是一致的
pa[l] = p;
return id;
}
终于写完了第一篇完整的博客了,这篇东西陆陆续续写了几天,从开始写到结束,拖了应该有半个月还是一个月,中间差点放弃,拖久了,知识的诅咒会越来越强,弄懂了之后就会越来越觉得好像也不难,没必要再写下去了,由于之前学linux也写了一些草稿,有些没头没尾,写到一半不想写了,有些纯学习笔记,最终就都沦为我的csdn在线学习笔记,所以还是比较有欲望发一篇原创博文,最终还是坚持下来了,由于隔了很多天再回看代码还是有些地方突然看不懂,这也越让我更坚定地觉得还是要把这篇东西完成,留下点自己思考的东西以后再看也有个记录作为参考。
第一篇博客,水平有限,有问题可以多多交流!
参考:
Linux Ida and Ird 源码分析_gjq_1988的博客-CSDN博客
ida和idr机制分析(盘符分配机制) - 自然技术搬运工 - 博客园
查找——图文翔解RadixTree(基数树) - 走看看