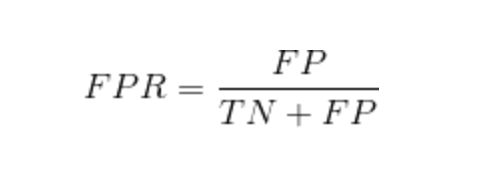RS Meet DL(75)-考虑CPM的评估方法csAUC

1、背景

在点击率预估中，AUC是最常用的评估指标，这一指标衡量的是任取一个正例和负例，正例的得分高于负例的概率。那么点击率预估中，正例和负例分别是什么呢？很显然，正例就是用户点击过的item，负例是用户没有点击的item。

但是在广告排序场景下，线上排序通常考虑收益最大化，通过CTR * Bid进行排序，而非仅仅通过CTR进行排序。如果线下仅仅通过AUC来评价离线模型的效果，你往往会发现，线下的AUC涨了，但是线上的收入eCPM（千次广告展示收入）却降了。这是因为线下AUC的评估仅考虑点击率CTR，而线上展示不仅考虑了CTR，同时考虑了广告主的出价BID，二者之间存在一定的gap。

因此，本文提出了考虑CPM的评估方法csAUC，下文中我们先回顾一下AUC的定义，再介绍csAUC。

2、AUC回顾

混淆矩阵
我们首先来看一下混淆矩阵，对于二分类问题，真实的样本标签有两类，我们学习器预测的类别有两类，那么根据二者的类别组合可以划分为四组，如下表所示：

上表即为混淆矩阵，其中，行表示预测的label值，列表示真实label值。TP，FP，FN，TN分别表示如下意思：

TP（true positive）：表示样本的真实类别为正，最后预测得到的结果也为正；
FP（false positive）：表示样本的真实类别为负，最后预测得到的结果却为正；
FN（false negative）：表示样本的真实类别为正，最后预测得到的结果却为负；
TN（true negative）：表示样本的真实类别为负，最后预测得到的结果也为负.

想要计算AUC，我们通常先绘制ROC曲线，ROC曲线的横轴为“假正例率”（False Positive Rate,FPR)，又称为“假阳率”；纵轴为“真正例率”(True Positive Rate,TPR)，又称为“真阳率”，

假阳率，简单通俗来理解就是预测为正样本但是预测错了的可能性：

真阳率，则是代表预测为正样本但是预测对了的可能性：

ROC计算过程如下：
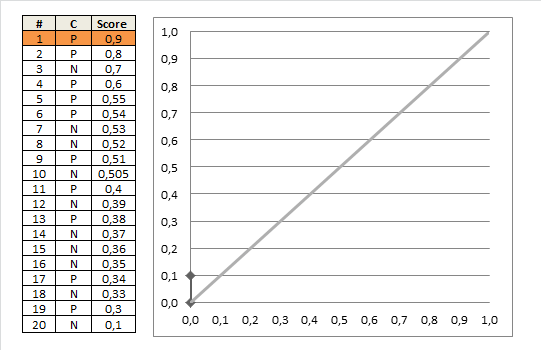
1)首先每个样本都需要有一个label值，并且还需要一个预测的score值（取值0到1）;
2)然后按这个score对样本由大到小进行排序，假设这些数据位于表格中的一列，从上到下依次降序;
3)现在从上到下按照样本点的取值进行划分，位于分界点上面的我们把它归为预测为正样本，位于分界点下面的归为负样本;
4)分别计算出此时的TPR和FPR，然后在图中绘制（FPR, TPR）点。

说这么多，不如直接看图来的简单：

AUC（area under the curve）就是ROC曲线下方的面积，如下图所示，阴影部分面积即为AUC的值：

AUC量化了ROC曲线表达的分类能力。这种分类能力是与概率、阈值紧密相关的，分类能力越好（AUC越大），那么输出概率越合理，排序的结果越合理。

AUC还有一个很有趣的性质，它和Wilcoxon-Mann-Witney是等价的，而Wilcoxon-Mann-Witney Test就是测试任意给一个正类样本和一个负类样本，正类样本的score有多大的概率大于负类样本的score。

根据这个定义我们可以来探讨一下二者为什么是等价的？首先我们偷换一下概念，其实意思还是一样的，任意给定一个负样本，所有正样本的score中有多大比例是大于该负类样本的score？ 那么对每个负样本来说，有多少的正样本的score比它的score大呢？是不是就是当结果按照score排序，阈值恰好为该负样本score时的真正例率TPR？理解到这一层，二者等价的关系也就豁然开朗了。ROC曲线下的面积或者说AUC的值 与 测试任意给一个正类样本和一个负类样本，正类样本的score有多大的概率大于负类样本的score是等价的。基于此，我们可以得到AUC的计算公式：

上式中，统计一下所有的 M×N(M为正类样本的数目，N为负类样本的数目)个正负样本对中，有多少个组中的正样本的score大于负样本的score。当二元组中正负样本的 score相等的时候，按照0.5计算。然后除以MN。

3、CPM-sensitive AUC

好了，回顾完AUC，本节介绍一下CPM-sensitive AUC（简称csAUC），这里，我们首先要对样本的级别进行划分：

样本级别是多层次的：AUC中样本仅有正例负例之分，但是在csAUC中，样本的排序是多层次的，负例是的level是最低的（lowest），而正例会按照其对应的bid进行排序，正例的bid越高，其level也是越高的。

给定一个high-level的样本xh和low-level的样本xl，定义收益（Rev）如下：

而整个样本集D中的csAUC计算如下：

对于一个给定的样本集D，csAUC的分母是确定的，对于分子来说，如果训练得到的模型没有将出价高的正样本排在出价低的正样本或者将负样本排在正样本前面的话，都会造成损失（分子减小），当两个正样本的出价相差越大，或者正样本出价越高（一正一负的情况），造成的损失越大。因此csAUC不仅希望正样本能够排在负样本前面，而且希望出价高的正样本排序能够更靠前。

4、csAUC分析

下面给出一个例子对AUC和csAUC进行分析，样例如下：

接下来给出六个模型，每个模型得到的排序结果如下：

各组结果的AUC及csAUC如下：

这里咱们一起来算下第一组结果的csAUC：

对于AUC来说，由于有M个正样本和N个负样本，因此构成的样本对只有M*N个(本例是4 * 1=4），但是对于csAUC来说，其样本对有10个（正样本里随机选两个的选法C2M + M * N，本例是C24 + 4 * 1 = 10）

可以看到，只要把所有正样本排在负样本前面，AUC都是1，所以只评价AUC的话，前4个模型的离线效果是相同的。但是第一个模型把出价最高的A排在了正样本的最后，造成了很多收益损失，所以其csAUC最低。

好了，本文的csAUC就介绍到这里了，对于此感兴趣的同学可以尝试一下哟～～