线性回归sklearn实现2

3.1 sklearn 回归实践

#绘制一条直线
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(-6,6,100)
y=0.5*x+2
plt.plot(x,y)

#已知两点，绘制一条直线
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
x=np.array([2,6])
y=np.array([3,5])
plt.plot(x,y)

#已知两个点，求直线斜率，（2，3），（6，5）
k=(y[1]-y[0])/(x[1]-x[0])
print(k)

0.5

一、sklearn 线性回归初体验

#导入sklearn中的线下回归模型
from sklearn.linear_model import LinearRegression
x=np.array([2,6])
y=np.array([3,5])
#导入回归模型实例化
lr=LinearRegression()
#模型训练
#lr.fit(x,y)
x=x.reshape(-1,1)#或者:x = np.array([[2]，[6]])
lr.fit(x,y)
print("过两点（2，3）,（6，5）的直线的斜率为:{},截距项为:{:.2f}".format(lr.coef_,lr.intercept_))

过两点（2，3）,（6，5）的直线的斜率为:[0.5],截距项为:2.00

#模型预测
x_test=np.array([3,4,5]).reshape(-1,1)
y_predict = lr.predict(x_test)
#y_predict 
#模型评估——计算R方值
lr.score(x,y)

1.0

#计算模型lr的均方误差
from sklearn.metrics import mean_squared_error
y=0.5*x_test+2
mean_squared_error(y,y_predict)

6.573840876841765e-32

#利用sklearn. datasets.make_regression生成用于回归分析的数据集
from sklearn.datasets import make_regression
X_3,y_3=make_regression(n_samples=100,n_features=1)
plt.scatter(X_3,y_3)

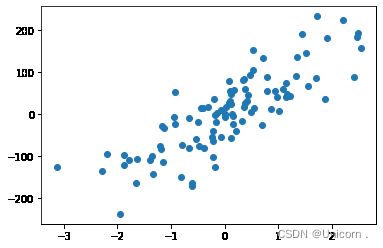
X_3,y_3=make_regression(n_samples=100,n_features=1,noise=50,random_state=8)
plt.scatter(X_3,y_3)

#利用线性回归模型对数据X_3,y_3进行拟合#模型实例化
reg = LinearRegression ()
#模型训练
reg.fit(X_3,y_3)
#绘制回归直线
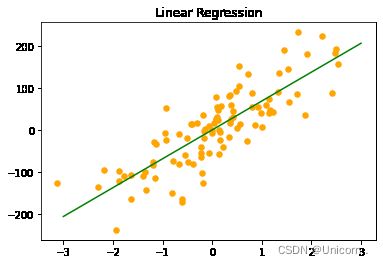
z = np.linspace(-3,3,200).reshape(-1,1)
plt.scatter(X_3,y_3,c='orange',s=30)
plt.plot(z, reg. predict(z), c='g')
plt.title('Linear Regression')
print("回归直线的斜率是:{:.2f} ".format(reg.coef_[0]))
print('回归直线的截距是:{:.2f} '.format(reg.intercept_))

回归直线的斜率是:68.78 
回归直线的截距是:1.25 

二、糖尿病数据集的线性回归分析

#导入糖尿病数据集
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
print(diabetes['DESCR'])

X=diabetes.data
y=diabetes.target
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=8)
lr = LinearRegression().fit(X_train,y_train)
print("训练数据集得分:{:.2f} ".format(lr.score(X_train,y_train)))
print("测试数据集得分:{:.2f} ".format(lr.score(X_test,y_test)))

训练数据集得分:0.53 
测试数据集得分:0.46 

三、岭回归

#岭回归
from sklearn.linear_model import Ridge
#模型实例化
ridge=Ridge()
#导入糖尿病数据集
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
X=diabetes.data#特征变量
y=diabetes.target#因变量
#划分训练集和测试集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_trian=train_test_split(X,y,random_state=8)
#模型训练
ridge.fit(X_train,y_train)
print("训练数据集得分:{:.2f} ".format(ridge.score(X_train,y_train)))
print("测试数据集得分:{:.2f} ".format(ridge.score(X_test,y_test)))

训练数据集得分:0.43 
测试数据集得分:0.43 

岭回归的参数调节

#正则化系数alpha=10
ridge10 = Ridge(alpha=10).fit(X_train,y_train)
print("训练数据集得分:{:.2f}".format(ridge10.score(X_train,y_train)))
print("测试数据集得分:{:.2f}".format(ridge10.score(X_test,y_test)))

训练数据集得分:0.15
测试数据集得分:0.16

#正则化系数alpha=0.1
ridge10 = Ridge(alpha=0.1).fit(X_train,y_train)
print("训练数据集得分:{:.2f}".format(ridge10.score(X_train,y_train)))
print("测试数据集得分:{:.2f}".format(ridge10.score(X_test,y_test)))

训练数据集得分:0.52
测试数据集得分:0.47

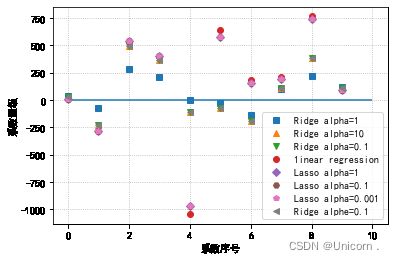
#模型系数的可视化比较
plt.plot(ridge.coef_,'s',label= 'Ridge alpha=1')
plt.plot(ridge10.coef_, '^',label= 'Ridge alpha=10')
plt.plot(ridge10.coef_, 'v', label = 'Ridge alpha=0.1')
plt.plot(lr.coef_, 'o', label= '1inear regression')
plt.xlabel("系数序号")
plt.ylabel("系数量级")
plt.hlines(0,0,len(lr.coef_))
plt.legend(loc='best')
plt.grid(linestyle=':')
plt.rcParams['font.sans-serif']=['SimHei','Times New Roman']
plt.rcParams['axes.unicode_minus']=False

from sklearn.model_selection import learning_curve,KFold
def plot_learning_curve(est,X,y):
    traning_set_size,train_scorse,test_scores=learning_curve(
        est,X,y,train_sizes=np.linspace(.1,1,20),cv=KFold(20,shuffle=True,
                                                         random_state=1))
        estimator_name=est._class_._name_
        line.plot(
        )

四、LASSO回归

from sklearn.linear_model import Lasso
#实例化
lasso=Lasso()
lasso.fit(X_train,y_train)
print("套索回归在训练集的得分:{:.2f}".format(lasso.score(X_train,y_train)))
print("套索回归在训练集的得分:{:.2f}".format(lasso.score(X_test,y_test)))

#特征选择
print("套索回归在训练集的得分:{}".format(np.sum(lasso.coef_!=0)))

套索回归在训练集的得分:0.36
套索回归在训练集的得分:0.37
套索回归在训练集的得分:3

LASSO回归的参数调节

#增加最大的次数默认设置，默认max_iter=100
#同时调整alpha的值
lasso=Lasso(alpha=0.1,max_iter=10000).fit(X_train,y_train)
print("alpha=0.1时套索回归在训练集的得分:{:.2f}".format(lasso.score(X_train,y_train)))
print("alpha=0.1时套索回归在训练集的得分:{:.2f}".format(lasso.score(X_test,y_test)))
#特征选择
print("alpha=0.1时套索回归在训练集的得分:{}".format(np.sum(lasso.coef_!=0)))

alpha=0.1时套索回归在训练集的得分:0.52
alpha=0.1时套索回归在训练集的得分:0.48
alpha=0.1时套索回归在训练集的得分:7

#增加最大的次数默认设置，默认max_iter=100
#同时调整alpha的值为0.001
lasso=Lasso(alpha=0.001,max_iter=10000).fit(X_train,y_train)
print("alpha=0.1时套索回归在训练集的得分:{:.2f}".format(lasso.score(X_train,y_train)))
print("alpha=0.1时套索回归在训练集的得分:{:.2f}".format(lasso.score(X_test,y_test)))
#特征选择
print("alpha=0.1时套索回归在训练集的得分:{}".format(np.sum(lasso.coef_!=0)))

alpha=0.1时套索回归在训练集的得分:0.53
alpha=0.1时套索回归在训练集的得分:0.46
alpha=0.1时套索回归在训练集的得分:10

#模型系数的可视化比较
plt.plot(ridge.coef_,'s',label= 'Ridge alpha=1')
plt.plot(ridge10.coef_, '^',label= 'Ridge alpha=10')
plt.plot(ridge10.coef_, 'v', label = 'Ridge alpha=0.1')
plt.plot(lr.coef_, 'o', label= '1inear regression')

plt.plot(lasso.coef_,'D',label= 'Lasso alpha=1')
plt.plot(lasso.coef_, 'H',label= 'Lasso alpha=0.1')
plt.plot(lasso.coef_, 'p', label = 'Lasso alpha=0.001')
plt.plot(ridge10.coef_, '<', label= 'Ridge alphe=0.1')

plt.xlabel("系数序号")
plt.ylabel("系数量级")
plt.hlines(0,0,len(lr.coef_))
plt.legend(loc='best')
plt.grid(linestyle=':')
plt.rcParams['font.sans-serif']=['SimHei','Times New Roman']
plt.rcParams['axes.unicode_minus']=False

3.2梯度下将法实践

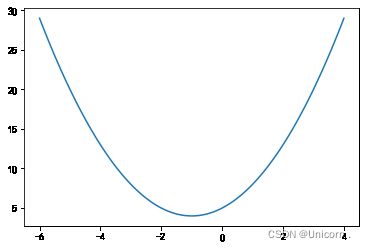
#绘制曲线
x=np.linspace(-6,4,100)
y=x**2+2*x+5
plt.plot(x,y)

x_iter=3
yita=0.06
count=0.06
while True:
    count +=1
    y_last = x_iter **2+ x_iter * 2+5
    x_iter = x_iter - yita * (2* x_iter + 2)
    y_next = x_iter**2 + x_iter *2+5
    plt.scatter(x_iter,x_iter**2+x_iter*2+5)
    if abs(y_next - y_last)<1e-100:
        break
print('最小值点x=', x_iter,'最小值y=',y_next,'迭代次数n=', count)
x=np.linspace(-5,3,100)
y=x**2+2*x+5
plt.plot(x,y)

最小值点x= -0.9999999594897632 最小值y= 4.000000000000002 迭代次数n= 144.06

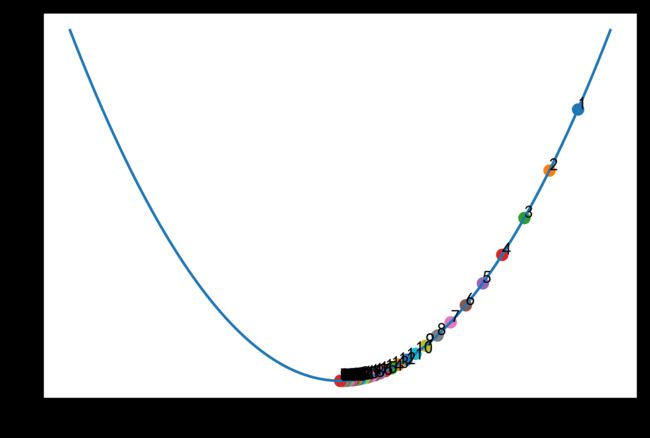
plt.figure(dpi=600)
x_iter=3
yita=0.06
count=0
while True:
    count +=1
    y_last = x_iter **2+ x_iter * 2+5
    x_iter = x_iter - yita * (2* x_iter + 2)
    y_next = x_iter**2 + x_iter *2+5
    plt.scatter(x_iter,x_iter**2+x_iter*2+5)
    plt.annotate(count,(x_iter,x_iter**2+x_iter*2+5))#标注各个点
    if abs(y_next - y_last)<1e-100:
        break
print('最小值点x=', x_iter,'最小值y=',y_next,'迭代次数n=', count)
x=np.linspace(-5,3,100)
y=x**2+2*x+5
plt.plot(x,y)

最小值点x= -0.9999999594897632 最小值y= 4.000000000000002 迭代次数n= 144

#修改步长为0.8
plt.figure(dpi=600)
x_iter=3#  x的初值
yita=0.8  #步长
count=0  #迭代次数
while True:
    count +=1
    y_last = x_iter **2+ x_iter * 2+5
    x_iter = x_iter - yita * (2* x_iter + 2)
    y_next = x_iter**2 + x_iter *2+5
    plt.scatter(x_iter,x_iter**2+x_iter*2+5)
    plt.annotate(count,(x_iter,x_iter**2+x_iter*2+5))#标注各个点
    if abs(y_next - y_last)<1e-100:
        break
print('最小值点x=', x_iter,'最小值y=',y_next,'迭代次数n=', count)
#绘制曲线
x=np.linspace(-5,3,100)
y=x**2+2*x+5
plt.plot(x,y)

最小值点x= -1.000000008911663 最小值y= 4.0 迭代次数n= 39