【剑指offer专项突破版】数组篇——“C“
文章目录
- 前言
- 一 . 排序数组中两个数字的和
-
- 题目分析
- 思路分析
-
- 法①代码——双指针
- 法②代码——二分查找
- 二. 数组中和为 0 的三个数
-
- 题目分析
- 问题转换
- 代码
- 三. 和大于等于 target 的最短子数组
-
- 题目分析
- 思路分析
- 代码
- 四. 乘积小于 K 的子数组
-
- 题目分析
- 思路分析
- 代码
- 五. 和为 k 的子数组
-
- 题目分析
- 思路分析
- 代码
- 六. 0 和 1 个数相同的子数组
-
- 题目分析
- 思路分析
- 代码
- 七. 左右两边子数组的和相等
-
- 题目分析
- 思路分析
- 代码
- 八. 二维子矩阵的和
-
- 题目分析
- 思路分析
- 代码
- 总结
前言
剑指offer专项突破版(力扣官网)——> 点击进入
本文所属专栏——>点击进入
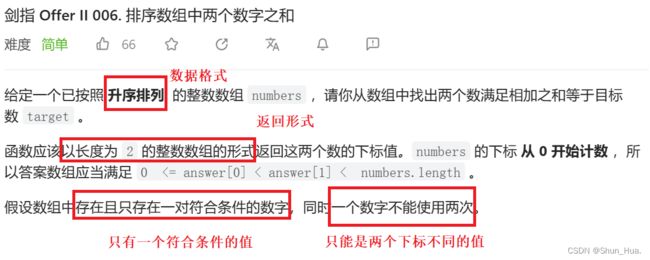
一 . 排序数组中两个数字的和
题目分析
思路分析
关键:利用好升序数组的特性
思路1:可以利用双指针,一个左下边标,一个右下标,这样比目标数大,就让右下标右移,调小。比目标数小,就让左下标左移,调大。
思路2:固定一个值(可以从左边也可以从右边),那么要找的数就是目标值-这个固定的值,这个固定的值就可以利用二分法进行查找。
法①代码——双指针
int* twoSum(int* numbers, int numbersSize, int target, int* returnSize)
{
//开辟空间并初始化数组
int *arr = (int*)malloc(sizeof(int)*2);
*returnSize = 2;
memset(arr,0,sizeof(int)*2);
//双指针查找思路
int left = 0;
int right = numbersSize - 1;
while(left < right)
{
int sum = numbers[left]+numbers[right];
if(sum > target)
{
right--;
}
else if(sum < target)
{
left++;
}
else
{
arr[0] = left;
arr[1] = right;
break;
}
}
return arr;
}
法②代码——二分查找
int* twoSum(int* numbers, int numbersSize, int target, int* returnSize)
{
//开辟空间并初始化数组
int *arr = (int*)malloc(sizeof(int)*2);
*returnSize = 2;
memset(arr,0,sizeof(int)*2);
//二分查找思路
for(int i = 0; i < numbersSize; i++)
{
//从左边开始
int left = i+1;
int right = numbersSize - 1;
int mid = (left+right)/2;
int Target = target - numbers[i];
int flag = 0;
while(left<=right)//这里是可以相等的,因为我要找的是一个数
{
if(numbers[mid]>Target)
{
right = mid - 1;
}
else if(numbers[mid]<Target)
{
left = mid + 1;
}
else
{
flag = 1;
break;
}
//更新mid
mid = (left+right)/2;
}
if(flag)
{
arr[0] = i;
arr[1] = mid;
break;
}
}
return arr;
}
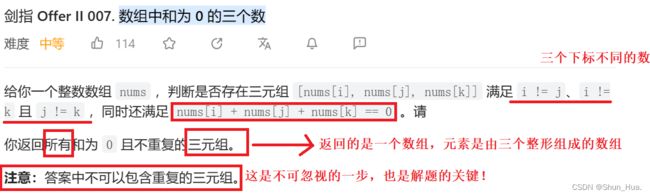
二. 数组中和为 0 的三个数
题目分析
- 总结
1.返回值——二维数组——元素为三个元素的数组
2.要求——找到三个不一样(下标)的数,使之相加等于0。
3.关键——返回的二维数组中的元素不能重复。
问题转换
要求是nums[i] + nums[j] + nums[k] == 0,那我们转换一下求满足 nums[j] + nums[k] == -nums[i] ,这样眼熟吗?不就是升序数组中两个数字和等于target吗?但是这个target也在数组中,于是我们要固定taget,然后再求这两个数,如何求呢?因为是升序数组,所以我们要先对数组进行排序。然后遍历数组依次取target,target固定一个边界,那么剩余的另一边的元素,就是我们用双指针的进行找两个元素的范围了。
剩下有两个细节,第一个——开空间直接开够,这里的的空间开够指的就是所有的可能性之和——从一个数组中选3个元素,不按顺序,有多少种排法?设数组的元素是size,利用高中知识,(size)*(size-1)/(3*2)就为所有可能性,因此我们至少要开这么大的空间;第二个——如何避免重复的三元组,那我们就要想到,为啥会产生重复的三元组?因为有重复的元素,那答案就是跳过重复的元素即可。
- 总结
第一步:对数组进行排序——qsort的使用
第二步: 开辟一个二维数组——空间足够
第三步:进行遍历取target并确定边界。
第四步:找值,找到存储——在一个三个元素的一维数组中。
第五步:调整值。
第六步:返回的一维数组初始化。
代码
int my_cmp(int* e1,int* e2)
{
return *e1 - *e2;
}
int** threeSum(int* nums, int numsSize, int* returnSize, int** returnColumnSizes)
{
//首先说明的是:returnColumnSizes是指向一维数组的指针的指针,
//因为要修改指针的指向,所以要传进去二级指针!
//第一步——将数组进行排序——升序
qsort(nums,numsSize,sizeof(int),my_cmp);
//第二步——将开辟一个二维数组
//分析:
//一次一次开的效耗比较大——realloc
//因此可以一下子把空间开够——那么数组中三个成组的所有可能性就为
//——从numsSize中选3个不排序
//因此为——numsSize*(numsSize-1)/(3*2*1)
int size = numsSize*(numsSize-1)/6;
int **arr =(int **)malloc(sizeof(int*)*size);
*returnSize = 0;//*returnSize表示有多少行
int cur_size = 0;
//第三步——查找指定的数字
//分析:
//根据nums[i]+nums[j]+nums[k]==0——>-nums[i] = nums[j]+nums[k]
//-nums[i]为固定的值,那么我们找的就是 nums[j]+nums[k] = -nums[i]
//说明:这里的numsize-2说的是最后剩下两个元素就不用进去了,没必要。
for(int i = 0; i<numsSize-2;)
{
//这是要找的条件
int target = -nums[i];
//双指针进行查找
int left = i+1;
int right = numsSize-1;
//printf("hehe");
while(left<right)
{
int sum = nums[left]+nums[right];
if(sum>target)
{
right--;//调小
}
else if(sum<target)
{
left++;//调大
}
else
{
//找到了
int va_l = nums[left];
int va_r = nums[right];
//开辟一个一维数组进行存储
int * tmp = (int*)malloc(sizeof(int)*3);
tmp[0] = nums[i];
tmp[1] = nums[left];
tmp[2] = nums[right];
//printf("%d",tmp[0]);
arr[cur_size++] = tmp;
*returnSize = cur_size;
//调整部分
//因为可能有重复多个,原因是存在相等的值,所以如果有要跳过
while(left<right&&nums[right]==va_r)
{
right--;
}
//这里的left可以不用动,因为只要一个动了,就会导致最后的sum
//也会变,之后的循环就会导致left也跟着变。
}
}
int va_i = nums[i];
//跳过target的相等的元素。
while((i<numsSize-2)&&(nums[i]==va_i))
{
i++;//至少进一次循环。
}
}
(*returnColumnSizes) = (int*)malloc(sizeof(int)*(*returnSize));
for(int i = 0; i<(*returnSize);i++)
{
(*returnColumnSizes)[i] = 3;
}
return arr;
}
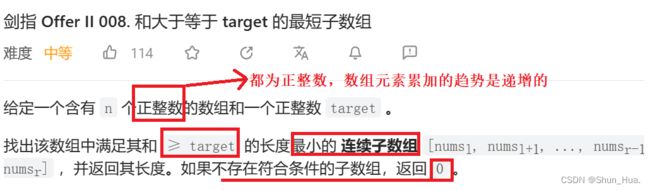
三. 和大于等于 target 的最短子数组
题目分析
1.数据格式——正整数,累加必定递增
2.要求——找到最小长度的连续子数组
3.返回——如果最小长度不存在,返回0,存在,则将最小长度返回。
思路分析
既然是累加递增,那就先累加,让其保持增长的趋势,如果大于target,那么就要判断这时的长度是否为当前最小的长度,如果是更新最小长度,然后继续找,怎么继续?那就让数组的左边元素不断的减,直到小于target即可。然后再进行上面的这一个动作,加直到大于target,然后再判断,再减。这样直到遍历完即可。
- 总结
第一步:确定两个边界,左边界和右边界。
第二步:让右边界一直增,直到大于判断,再更新左边界。
第三步:返回最小的长度即可。
代码
int minSubArrayLen(int target, int* nums, int numsSize)
{
int min_len = 0;
int left = 0;
int sum = 0;
for(int right = 0; right < numsSize; right++)
{
sum+=nums[right];
//这里的left==right时,是当right与left之间只有一个数字时的情况判断。
while(sum>=target&&left<=right)
{
int len = right - left + 1;
//这需要注意的是当min_len == 0时也得进去。
if(min_len > len || min_len == 0)
{
min_len = len;
}
sum-=nums[left++];
}
}
return min_len;
}
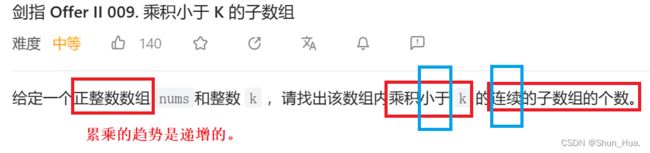
四. 乘积小于 K 的子数组
题目分析
- 总结:
1.数据格式——正整数数组——累乘的趋势是递增的。
2.要求——求出小于k的连续子数组的个数。
3.返回值——连续的的子数组的个数。
思路分析
既然是累乘的趋势也是递增的,那我们当小于k时,求出连续的子数组的个数不就行了,当大于k时,就当乘积除以左边的边界,直到小于就跳出循环,但是怎么求连续的子数组的个数呢?我们可以这样想,假如有数组中有前n个数的乘积都小于k,再增加1个数的之后的乘积还小于k,这时新增的连续的子数组的个数怎么求呢,不就是n+1或者说数组的长度吗?怎么算的呢?
举个简单的例子:
| 当前数组 | 新增数组 | 新增的连续子数组 |
|---|---|---|
| [1 , 2] | [1,2,3] | [3], [2,3], [1, 2,3] |
看懂了吗? 从最后一个数往前数有几个数就新增了几个子数组。
于是我们只需求每次新增了几个子数组即可。
- 总结
第一步:求乘积,定义左边界与右边界——都从0下标开始
第二步:当大于k时,就调整到小于k
第三步: 当小于k时,就计算新增的子数组。
第四步:循环结束,返回子数组的个数。
代码
int numSubarrayProductLessThanK(int* nums, int numsSize, int k)
{
//乘积
int sum_product = 1;
//子数组的个数
int count = 0;
//左边界
int left = 0;
for(int right = 0; right < numsSize; right++)
{
sum_product*=nums[right];
//判断是否大于k,并且需注意前提left<=right
while(left<=right&&sum_product>=k)
{
sum_product/=nums[left++];
}
//这里sum_product必定小于target,因此只需计算新增的个数即可
count+=(right-left+1);
//注意:当left -1 == right-> right-left +1 ==0 时,
//——刚好新增的个数为0。
}
return count;
}
五. 和为 k 的子数组
题目分析
- 总结
1.数据格式——整数——累加的趋势不确定,因此无法用双指针进行解题。
2.要求——找到和为k的连续的子数组。
3.返回——符合要求的子数组的个数。
思路分析
既然无法用双指针,就只能暴力求解了吗?很显然暴力求解是行不通的,如果,有这样一种方法,如果直到前n个数字的和——sum,那么如果前n个数中的第1到j个数相加满足sum-k,那么从第j+1个数到第n个数就是我们要求的k了,那么sum-k出现的次数就是我们要求得的子数组的个数。
图解:

如果我们有这样的一个数组,可以存储sum-k出现的次数,然后通过sun-k找到次数,再加上就可以了,当我们边找边存的时候,就可以忽略一个条件,下标的比较。因此我们需要一个哈希表,键值(下标)是sum-k,找的是sum-k出现的次数。
代码
~这里手搓了一个简单的哈希表,虽然能过,但是效率很低。这里以后会补充其它解法的。
typedef struct HashNode
{
int count;//次数
struct HashNode* next;
}HN;
int Hash_Key(int x)
{
return x+200000;
}
int find_key(HN**arr,int x,int index)
{
int key = Hash_Key(x);
HN * judge = arr[key];
if(judge==NULL)
{
return 0;
}
return (judge)->count;
}
void PushBack(HN **arr,int key,int index)
{
HN* NewNode =(HN*)malloc(sizeof(HN));
NewNode->count = 0;
NewNode->next = NULL;
if(arr[key]==NULL)
{
NewNode->count = 1;
arr[key]=NewNode;
return;
}
else
{
HN* cur = arr[key];
(cur->count)++;
}
free(NewNode);
}
//最后销毁一下,偷个懒,知道就行
void Destory(HN**arr)
{
}
int subarraySum(int* nums, int numsSize, int k)
{
HN **arr = (HN**)malloc(sizeof(HN*)*30000001);
memset(arr,0,sizeof(HN*)*30000001);
//首先计算和并存入表中
int sum = 0;
int target = 0;
int count = 0;
for(int i = 0; i < numsSize; i++)
{
sum+=nums[i];
target = sum-k;
int ret = find_key(arr,target,i);
if(sum==k)
{
count++;
}
count+=ret;
PushBack(arr,Hash_Key(sum),i);//这里要最后再插入,避免影响
}
Destory(arr);
return count;
}
六. 0 和 1 个数相同的子数组
题目分析
- 总结
1.数据格式——0 1
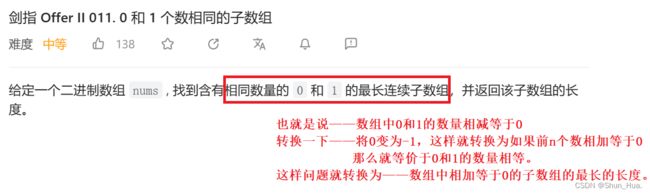
2.要求——找到相同数量的0和1的最长连续的子数组
3.返回要求——返回符合要求的子数组的长度。
思路分析
将题目转换为,数组相加等于0的子数组的最长的长度。也就是将第五题的思路移到下面,不过需要注意的是,键值虽然还是和,但是里面的值可是最小的下标。
代码
~这里也是手搓的一个简单的哈希表,不过跟上面不同的是,这里只需有一个下标即可,如果原来的位置有就看是不是最小的,如果不是最小的,那就更新下标值。
typedef struct HashNode
{
int i;//下标位置
struct HashNode* next;
}HN;
int Hash_Key(int x)
{
return x+100000;
}
int find_key(HN**arr,int x,int index)
{
int key = Hash_Key(x);
HN * judge = arr[key];
if(judge==NULL)
{
return -1;
}
int smaller = -1;
HN* cur = arr[key];
int i = cur->i;
if(i<index)
{
smaller = i;
}
return smaller;
}
void PushBack(HN **arr,int key,int index)
{
HN* NewNode =(HN*)malloc(sizeof(HN));
NewNode->i = index;
NewNode->next = NULL;
if(arr[key]==NULL)
{
arr[key]=NewNode;
return;
}
//因为是index是递增的,所以不需要再进行判断了,直接free即可
// else
// {
// HN* cur = arr[key];
// if(indexi)
// {
// cur->i = index;
// }
// }
free(NewNode);
}
//最后销毁一下
void Destory(HN**arr)
{
}
int findMaxLength(int* nums, int numsSize)
{
HN **arr = (HN**)malloc(sizeof(HN*)*200001);
memset(arr,0,sizeof(HN*)*200001);
int sum = 0;
int target = 0;
int max_len = 0;
for(int i = 0; i < numsSize; i++)
{
sum += nums[i] == 0 ? -1 : 1;
target = sum;
int left = find_key(arr,target,i);
if(left!=-1)
{
int len = i-left;//左开右闭
if(len>max_len)
{
max_len = len;
}
}
if(sum==0)
{
max_len = i+1;
}
//这里要最后再插入,避免影响
PushBack(arr,Hash_Key(sum),i);
}
Destory(arr);
return max_len;
}
七. 左右两边子数组的和相等
题目分析
- 总结
1.数据格式——整数
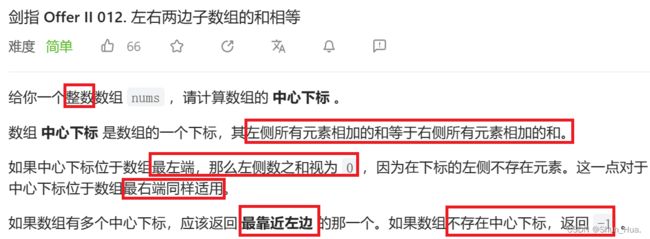
2.要求——求最左边的的中心下标
3.返回值——如果不存在返回-1,否则返回符合要求的中心下标
4.特殊情况:如果在最左边,那么其左边元素之和视为0。右边同理。
思路分析
首先暴力求解不可取,那么如何求解呢?根据中心下标左边之和等于右边之和,很显然右边之和又等于 整体之和减去左边之和与中心下标元素之和。那么我们只需要遍历一遍数组求出前n个数字的和,再运用前n个数字的和遍历数组利用上面的条件即可求解。
- 总结
第一步:求出前n个数字的和。
第二步:定义sum(左边之和加上中心下标元素)变量,循环遍历数组。
第三步:利用条件判断是否相等,相等则跳出循环,否则继续遍历。
第四步:返回中心下标。
代码
int pivotIndex(int* nums, int numsSize)
{
int tar_index = -1;
//求前n个数字之和
int sum = 0;
for(int i = 0; i < numsSize; i++)
{
sum += nums[i];
}
int cur_sum = 0;//就等于左边的和 + 中心下标
for(int i = 0; i < numsSize; i++)
{
cur_sum += nums[i];
//左边的和
int left = cur_sum - nums[i];
//右边的和
int right = sum - cur_sum;
if(right == left)
{
tar_index = i;
break;
}
}
return tar_index;
}
八. 二维子矩阵的和
题目分析
- 总结
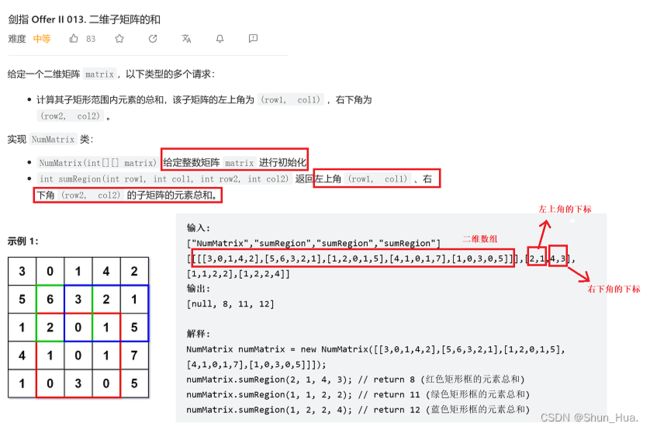
要求:
1.完成对二维数组——存放在结构体中的初始化
2.完成图中的求和工作
3.对结构体的空间进行释放
思路分析
首先开门见山,关键在于求和工作,其它的没那么难,不用想了暴力求解肯定不行,那咋求?
图解:

补充:如何求(0,0)到(i,j)的长度,比如一个数组是这样的。

- 总结:
1.开辟一个求和数组(存放求和结果)——比原来的要求和的数组多上1行1列
2.利用求和公式求解即可。
代码
typedef struct
{
int **arr;
int matrix;
int *matrixColSize;
int **sum;
} NumMatrix;
NumMatrix* numMatrixCreate(int** matrix, int matrixSize, int* matrixColSize)
{
//一行含有多少个元素
int colsize = matrixColSize[0];
NumMatrix* tmp = (NumMatrix*)malloc(sizeof(NumMatrix));
tmp->arr = (int**)malloc(sizeof(int*)*matrixSize);
tmp->matrix = matrixSize;
tmp->matrixColSize = (int*)malloc(sizeof(int)*matrixSize);
tmp->sum = (int**)malloc(sizeof(int*)*(matrixSize+1));
//首先要开辟一行
int * col = (int*)malloc(sizeof(int)*(colsize+1));
memset(col,0,sizeof(int)*(colsize+1));
(tmp->sum)[0] = col;
for(int i = 0; i < matrixSize; i++)
{
(tmp->matrixColSize)[i] = colsize;
}
//进行初始化,并完成求和工作
for(int i = 0; i < matrixSize; i++)
{
int * col_sum = (int*)malloc(sizeof(int)*(colsize+1));
memset(col_sum,0,sizeof(int)*(colsize+1));
int * col = (int*)malloc(sizeof(int)*colsize);
//定义求和变量
int sum = 0;
for(int j = 0; j < colsize; j++)
{
//完成累加操作
sum+=matrix[i][j];
//完成赋值操作
col[j] = matrix[i][j];
//完成求和操作
col_sum[j+1] = sum + (tmp->sum)[i][j+1];
}
//完成赋值
(tmp->arr)[i] = col;
(tmp->sum)[i+1] = col_sum;
}
return tmp;
}
int numMatrixSumRegion(NumMatrix* obj, int row1, int col1, int row2, int col2)
{
int **arr = obj->sum;
//arr[row2][col2]-arr[row1-1][col2]-arr[row2][col1-1]+arr[row1-1][col1-1]-在此基础上加一即可
int sum = arr[row2+1][col2+1]\
-arr[row1][col2+1]-arr[row2+1][col1] + arr[row1][col1];
return sum;
}
void numMatrixFree(NumMatrix* obj)
{
int **arr = obj->arr;
int **sum = obj->sum;
int * col = obj->matrixColSize;
free(sum);
free(arr);
free(col);
}
总结
- 前四道题,可以说是将双指针的用法展现的淋漓尽致。
- 第五道和第六道大同小异,不过都是得用哈希表存储,这样的效率会高一些。
- 第七道和第八道的思路雷同,不过是一维到二维而已。
- 第五道到第八道的解题思路很相似,可以说都跟求和有关,但是对求和的使用场景却不一样。
- 有些题看起来不一样,但是可以奇妙的转换成相同的思路,这就是灵活运用!
最后希望这篇文章对您有所帮助!