2023年第二十届五一数学建模竞赛 B题：快递需求分析问题

网络购物作为一种重要的消费方式，带动着快递服务需求飞速增长，为我国经济发展做出了重要贡献。准确地预测快递运输需求数量对于快递公司布局仓库站点、节约存储成本、规划运输线路等具有重要的意义。附件1、附件2、附件3为国内某快递公司记录的部分城市之间的快递运输数据，包括发货日期、发货城市以及收货城市(城市名已用字母代替，剔除了6月、11月、12月的数据)。请依据附件数据，建立数学模型，完成以下问题：

问题1：附件1为该快递公司记录的2018年4月19日—2019年4月17日的站点城市之间(发货城市-收货城市)的快递运输数据，请从收货量、发货量、快递数量增长/减少趋势、相关性等多角度考虑，建立数学模型，对各站点城市的重要程度进行综合排序，并给出重要程度排名前5的站点城市名称，将结果填入表1。

表1 问题1结果

排序	1	2	3	4	5
城市名称

问题2：请利用附件1数据，建立数学模型，预测2019年4月18日和2019年4月19日各“发货-收货”站点城市之间快递运输数量，以及当日所有“发货-收货”站点城市之间的总快递运输数量，并在表2中填入指定的站点城市之间的快递运输数量，以及当日所有“发货-收货”站点城市之间的总快递运输数量。

表2 问题2结果

日期	“发货-收货”城市之间的快递运输数量		所有“发货-收货”城市之间的总快递运输数量
2019年4月18日	M-U
	Q-V
	K-L
	G-V
2019年4月19日	V-G
	A-Q
	D-A
	L-K

问题3：附件2为该快递公司记录的2020年4月28日—2023年4月27日的快递运输数量。由于受到突发事件影响，部分城市之间快递线路无法正常运输，导致站点城市之间无法正常发货或收货(无数据表示无法正常收发货，0表示无发货需求)。请利用附件2数据，建立数学模型，预测2023年4月28日和2023年4月29日可正常“发货-收货”的站点城市对(发货城市-收货城市)，并判断表3中指定的站点城市对是否能正常发货，如果能正常发货，给出对应的快递运输数量，并将结果填入表3。

表3 问题3结果

日期	“发货-收货”站点城市对	是否能正常发货 (填写“是”或“否”)	快递运输数量
2023年4月28日	I-S
	M-G
	S-Q
	V-A
	Y-L
2023年4月29日	D-R
	J-K
	Q-O
	U-O
	Y-W

问题4：图1给出了所有站点城市间的铁路运输网络，铁路运输成本由以下公式计算：成本=固定成本×1+实际装货量额定装货量3正在上传…重新上传取消 。在本题中，假设实际装货量允许超过额定装货量。所有铁路的固定成本、额定装货量在附件3中给出。在运输快递时，要求每个“发货-收货”站点城市对之间使用的路径数不超过5条，请建立数学模型，给出该快递公司成本最低的运输方案。利用附件2和附件3的数据，计算该公司2023年4月23—27日每日的最低运输成本，填入表4。

备注：为了方便计算，不对快递重量和大小进行区分，假设每件快递的重量为单位1。仅考虑运输成本，不考虑中转等其它成本。

正在上传…重新上传取消

图1 站点城市间铁路运输网络

表4 问题4结果

日期	最低运输成本
2023年4月23日
2023年4月24日
2023年4月25日
2023年4月26日
2023年4月27日

问题5：通常情况下，快递需求由两部分组成，一部分为固定需求，这部分需求来源于日常必要的网购消费(一般不能简单的认定为快递需求历史数据的最小值，通常小于需求的最小值)；另一部分为非固定需求，这部分需求通常有较大波动，受时间等因素的影响较大。假设在同一季度中，同一“发货-收货”站点城市对的固定需求为一确定常数(以下简称为固定需求常数)；同一“发货-收货”站点城市对的非固定需求服从某概率分布(该分布的均值和标准差分别称为非固定需求均值、非固定需求标准差)。请利用附件2中的数据，不考虑已剔除数据、无发货需求数据、无法正常发货数据，解决以下问题。

(1) 建立数学模型，按季度估计固定需求常数，并验证其准确性。将指定季度、指定“发货-收货”站点城市对的固定需求常数，以及当季度所有“发货-收货”城市对的固定需求常数总和，填入表5。

(2) 给出非固定需求概率分布估计方法，并将指定季度、指定“发货-收货”站点城市对的非固定需求均值、标准差，以及当季度所有“发货-收货”城市对的非固定需求均值总和、非固定需求标准差总和，填入表5。

表5 问题5结果

季度	2022年第三季度 (7—9月)		2023年第一季度 (1—3月)
“发货-收货”站点城市对	V-N	V-Q	J-I	O-G
固定需求常数
非固定需求均值
非固定需求标准差
固定需求常数总和
非固定需求均值总和
非固定需求标准差总和

第一问代码

表1 问题1结果

排序	1	2	3	4	5
城市名称	L	G	V	X	J

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.sans-serif'] = 'SimHei' # 设置中文显示
plt.rcParams['axes.unicode_minus'] = False


df = pd.read_excel('附件1(Attachment 1)2023-51MCM-Problem B.xlsx')
df = ***{'日期(年/月/日) (Date Y/M/D)':'日期', '发货城市 (Delivering city)':'发货城市', '收货城市 (Receiving city)':
                       '收货城市', '快递运输数量(件) (Express delivery quantity (PCS))':'快递运输数量'})
df.head()


********

********
plt.grid(True)
plt.plot(x,y)
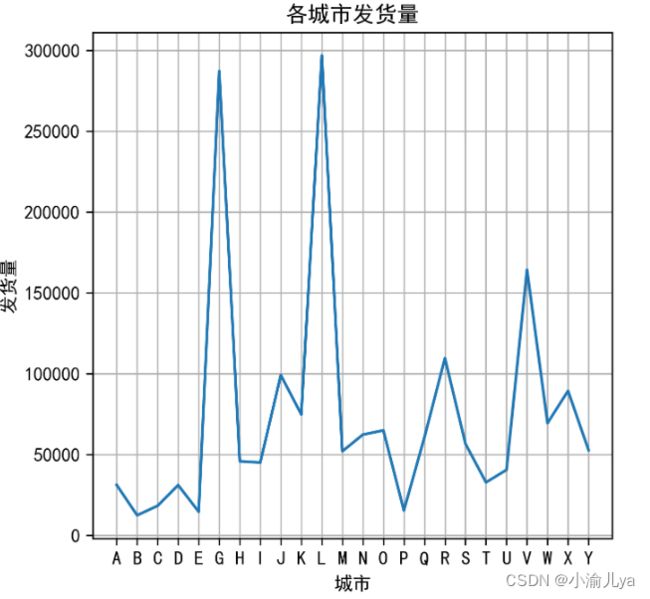
plt.ylabel('发货量')
plt.xlabel('城市')
plt.title('各城市发货量')
plt.savefig('各城市发货量.png',bbox_inches = 'tight')
plt.show()

*************


*********
plt.plot(x,y)
plt.ylabel('收货量')
plt.xlabel('城市')
plt.title('各城市收货量')
plt.savefig('各城市收货量.png',bbox_inches = 'tight')
plt.show()

**************
# 提取2019年4月数据
************

# 提取2018年4月数据
*********


**********
plt.figure(figsize=(5,5), dpi =300)
plt.grid(True)
plt.scatter(x_1,y_1,label='2018.4月各城市发货量')
plt.scatter(x_2,y_2,label='2019.4月各城市发货量')
plt.ylabel('发货量')
plt.xlabel('城市')
plt.title('各城市发货量')
plt.legend()
***********
plt.savefig('2018 2019年4月各城市发货量对比.png',bbox_inches = 'tight')
plt.show()

 

***********
plt.figure(figsize=(5,5), dpi =300)
plt.grid(True)
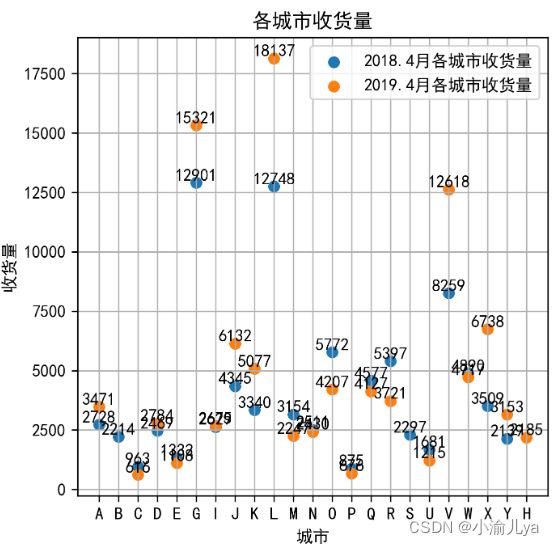
plt.scatter(x_1,y_1,label='2018.4月各城市收货量')
plt.scatter(x_2,y_2,label='2019.4月各城市收货量')
plt.ylabel('收货量')
plt.xlabel('城市')
plt.title('各城市收货量')
plt.legend()
***********
plt.savefig('2018 2019年4月各城市收货量对比.png',bbox_inches = 'tight')
plt.show()

# 整理数据
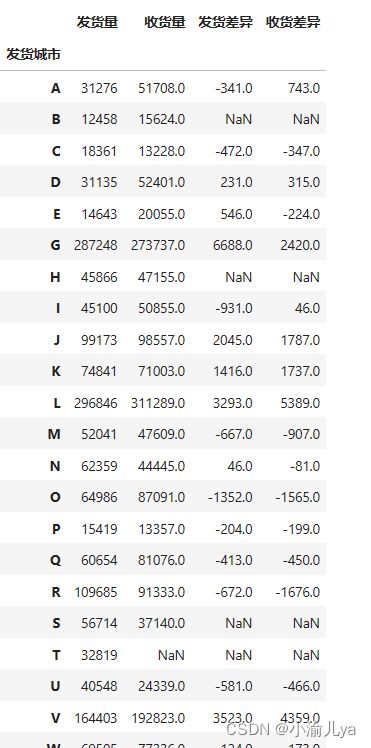
data= pd.DataFrame()
data['发货量'] = *
data['收货量'] = *
data['发货差异'] = *
data['收货差异'] = *

# 原始数据正向化
def func_1(x):
    return(x.max()-x) # 极小型
def func_2(x,x_best):
*
    y = []
    for i in x:
        if i < a:
            y.append(1-(a-i)/M)
        elif i > b:
            y.append(1-(i-b)/M)
        else:
            y.append(1) 
    return(y) # 区间型

# 标准化
def func(data):
    tep_x1 = (dat*
    return(Z)

data_bzh = func(data)

# 熵权法求每个指标权值
P = data_bzh/np.tile*1)) # 概率矩阵P
E = -1/np*.shape[0]) * (P*np.log(P)).sum()
D = 1-E
W = D/D.sum() # 熵权

tep_max = data_bzh.max()
*, (data_bzh.shape[0],1))).sum(axis = 1))**0.5
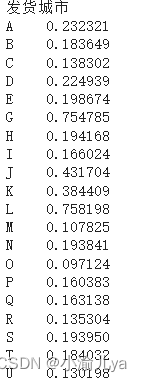
S = D_N/(D_P+D_N) # 未归一化得分

 

x = S.index
y = S.values
plt.figure(figsize=(10, 5) ,dpi=300)
plt.bar(x, y,  color= 'c')
plt.title('各城市重要程度得分排名', fontsize=13)
plt.xlabel('城市', fontsize=10)
plt.ylabel('得分', fontsize=10)
plt.xticks(rotation = 60) # 旋转坐标轴
plt.grid(True)
*
plt.savefig('各城市重要程度得分排名.png',bbox_inches = 'tight')
plt.show()

 

最后得出结论排名前五城市为G L V X J