算法与数据结构(五)
一、c++二叉树结构
typedef struct BiNode
{
int data; //结点内值域
struct BiNode* lchild, * rchild; //左孩子 右孩子
} BiNode, * BiTree;
或者:
class Node
{
public:
char data;// data表示该节点代表的内容;
Node* L;//左子树
Node* R;//右子树
};
Node* T;//创个指针,指向二叉树的根节点;
二、用递归和非递归两种方式实现二叉树的先序、中序、后序遍历
递归方法:
先序遍历:
先遍历头,再遍历左子树的结点、再遍历右子树的结点,遍历结果如下:
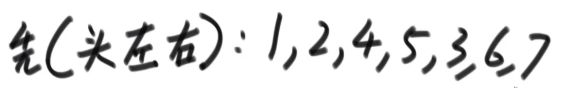
递归方法代码如下:
void preOrder(Node*& T)
{
if (T == NULL)
{
return;//如果该结点为空就返回;
}
//递归遍历
else
{
cout << T->data << " "; //先输出根节点的那个数字
preOrder(T->L); //然后访问左孩子,开始递归
preOrder(T->R); //左孩子访问完成,开始右孩子递归
}
}
以上代码输出即为先遍历
递归序的遍历结果为:

我们只需要在递归遍历过程中数字第一次出现时打印即可。
非递归:
思路:
先将根节点放到栈中
1、然后从栈中弹出一个结点cur
2、打印cur;
3、先右再左(如果有),否则什么也不做
4、循环1-3,直至栈中没有数据为止。
class Solution {
public:
void preorderTraversal(TreeNode* root) {
if(root != NULL){
//申请一个临时栈
stack<TreeNode*> st;
//将根节点首先压入栈中
st.push(root);
//如果栈不为空,则开始循环
while(!st.empty())
{ //弹出栈中的一个结点
root = st.pop();
//打印弹出的结点
cout << root->val << " ";
//如果叶结点不为空,则开始先将出栈节点的右结点和左结点先后压入栈中
if(root->right != NULL)
{
st.push(root->right);
}
if(root->left != NULL)
{
st.push(root->left);
}
}
}
}
中序遍历:
先遍历左,再遍历头的结点、再遍历右子树的结点,遍历结果如下:

递归方法代码如下:
void inOrder(Node*& T)
{
if (T == NULL)
return;
else
{
inOrder(T->L);
cout << T->data << " ";
inOrder(T->R);
}
}
非递归方法:
思路:
1、将压入结点下的每颗子树整棵树左边界进栈(第一次先从根节点开始),对于下图,进栈的为(1,2,4)
2、弹出结点,弹出的过程中对弹出结点打印
3、压入弹出节点的右结点
4、循环以上两个步骤

class Solution {
public:
void inOrderTraversal(TreeNode* root) {
if(root != NULL){
//申请一个临时栈
stack<TreeNode*> st;
//如果栈不为空,则开始循环
while(!st.empty() || root != NULL)
{
//如果当前结点不为空,则一直将其左结点压栈
if(root != NULL){
st.push(root);
root = root->left;
}
//否则从栈中弹出一个结点,并打印,将其右结点返回
else{
root = st.pop();
cout << root->val << " ";
root = root->right;
}
}
}
}
后序遍历:
先遍历左,再遍历右、再遍历头结点,遍历结果如下:

递归方法代码如下:
void posOrder(Node*& T)
{
if (T == NULL)
return;
else
{
posOrder(T->L);
posOrder(T->R);
cout << T->data << " ";
}
}
非递归方法:
思路:
先将根节点放到栈中
1、然后从栈中弹出一个结点cur
2、将弹出的结点放到一个回收栈中;
3、先左再右(如果有),否则什么也不做
4、循环1-3,直至栈中没有数据为止。
5、挨个从回收栈中弹出数据并打印
class Solution {
public:
void posOrderTraversal(TreeNode* root) {
if(root != NULL){
//申请一个临时栈
stack<TreeNode*> st1;
stack<TreeNode*> st2;
//将根节点首先压入栈中
st1.push(root);
//如果栈不为空,则开始循环
while(!st1.empty())
{ //弹出栈中的一个结点
root = st1.pop();
//将弹出的结点压入回收栈中
st2.push(root);
//如果叶结点不为空,则开始先将出栈节点的左结点和右结点先后压入栈中
if(root->left != NULL)
{
st1.push(root->left);
}
if(root->right != NULL)
{
st1.push(root->right);
}
}
//将回收栈中的数据打印
while(!st2.empty())
{
cout<<st2.pop()->val<< " ";
}
}
}
三、二叉树的宽度优先遍历(常见题目:求一棵二叉树的宽度)
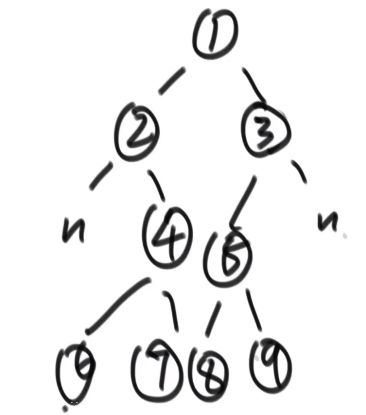
有如上的树。宽度优先遍历输出为:1,2,3,4,5,6,7,8,9
思路:
本题我们使用队列的方式来解决:
1、首先将根节点放到队列中
2、弹出队列中的第一个结点,然后打印该结点,并将该节点的左右子节点先后放到队列中(没有左或者右则直接跳过放另外一个结点)。
3、重复步骤二知道队列为空
#include四、求二叉树的最大宽度
思路:
1)、首先,我们需要知道每一个节点的层数:每一个节点的层数是其父节点层数+1所以,我们在push一个节点的孩子节点进入队列时,可以保存其孩子节点的层级:当前层级+1。
2)、其次,我们需要获取每一层的宽度,并所有层级宽度取最大值返回。因为宽度遍历方式相同层级的节点肯定是依次输出遍历,我们就很方便对某层宽度进行计数。
int MaxWidth(TreeNode* root)
{
int widMax = 0; //记录结果:最大宽度
if (nullptr == root)
{
return 0;
}
queue<TreeNode*> nodeQueue; //遍历二叉树的辅助队列
unordered_map< TreeNode*, int> levelMap; //记录每个节点所在层数的哈希表
//根节点入队列
nodeQueue.push(root);
levelMap[root] = 1; //根节点定义为在第1层
int curLevel = 1; //当前所在层数
int curWidth = 0; //当前层记录的宽度
while (!nodeQueue.empty())
{
TreeNode* temp = nodeQueue.front();
//弹出队首节点
nodeQueue.pop();
//获取队首节点的层数,如果和上一个队首节点的层数curLevel相同,则curWidth+1;否则,说明已经开始进入下一层,则重置curWidth并更新curLevel
if (levelMap[temp] == curLevel)
{
++curWidth;
}
//已经进入下一层
else
{
//在进入下一层结点之前先要保存最大宽度
widMax = curWidth > widMax ? curWidth : widMax;
//将宽度置一
curWidth = 1;
//重置层数
curLevel = levelMap[temp];
}
if (temp->left != NULL)
{
nodeQueue.push(temp->left);
//保存当前节点左孩子的层数:当前层数+1
levelMap[temp->left] = curLevel + 1;
}
if (temp->right != NULL)
{
nodeQueue.push(temp->right);
//保存当前节点右孩子的层数:当前层数+1
levelMap[temp->right] = curLevel + 1;
}
}
return widMax;
}
我们也可以不使用哈希表来实现这种操作。
思路:
1)进队列
2)cur_end记录最后一个结点
next_end记录每次进队列的结点
curlevel记录每层结点个数
3)每当出来的结点不等cur_end时,curlevel++;
每当出来的结点等于cur_end时,curlevel++,并将next_end赋给cur_end,next_end置为NULL,
max更新与curlevel比较,curlevel置为0
#include五、如何判断一颗二叉树是搜索二叉树
搜索二叉树:左侧结点都比头节点小,右侧结点都比头节点大。经典搜索二叉树没有重复值。

上图即为经典搜索二叉树。从上图可以看出,在中序遍历中,所有结点都是升序的,即为搜索二叉树。如果某一位置是降序的,则该树就不是搜索二叉树。
法一:直接通过递归的方式挨个子树遍历比较。
/*
* 概念:每个结点都比左儿子大,比右儿子小,严格的搜索二叉树没有重复的值
step: 1)中序遍历得到的数组的升序的
*/
int preData = INT_MIN;
bool isBST(Node* head) {
if (head == NULL)
return true;
bool isLeftBST = isBST(head->left);
if (!isLeftBST)//如果左树不是,就直接返回false
return false;
if (preData >= head->data)//如果根的data比左的小,就返回false
return false;
else {
preData = head->data;
}
return isBST(head->right);
}
法二:将每次中序遍历的结点全放到list容器中,然后再判断list容器中结点的值是否为升序。
//判断是否为搜索二叉树2
#include
#include法三:非递归过程中进行比较
bool isBST(node* head){
if (head == NULL){
return true;
}
stack<node*>newstack;
int pre = INT_MIN;
while (!newstack.empty() || head != NULL){
if (head != NULL){
newstack.push(head);
head = head->left;
}
else{
head = newstack.top();
//cout << head->value << ",";
if (pre < head->value){
pre = head->value;
}else{
return false;
}
newstack.pop();
head = head->right;
}
}
return true;
}

