【C语言】数据结构实验报告--单链表
实验内容
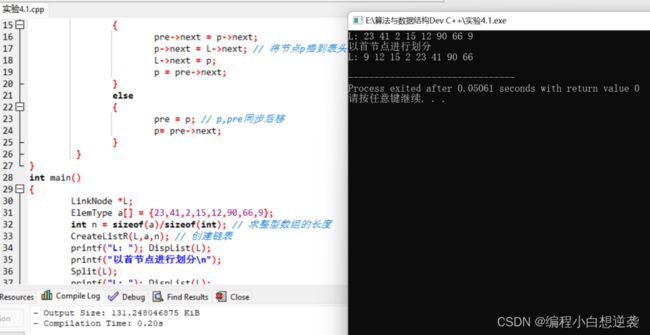
一.将单链表按基准划分,以单链表的首节点值x为基准将该单链表分割为两部分,使所有小于x的结点排在大于或等于x的结点之前。
#include这里的linklist.cpp是一个单独保存单链表所有基本操作的C文件
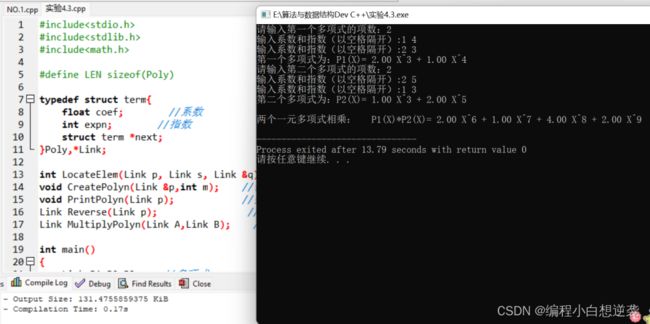
#include三.实现两个多项式相乘,用单链表存储一元单项式,并实现两个多项式相乘的运算
#include运行结果: