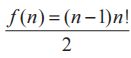数学，究竟美在哪里？
美的线条和其他一切美的形体都必须有对称的形式。
——毕达哥拉斯
艺术与科学，都是对称与不对称的巧妙组合。
——李政道
如果有人问我：“孩子在小学阶段应该培养什么数学思维？”，我会毫不犹豫地回答：有序思维和对称思维。
大自然对于“对称”似乎特别钟爱（图 6.1）。大家多多体会大自然的造物规律，在意识深处播下一粒理性思维的种子，这要比多刷几本习题集有意义得多。
当人们谈论对称的时候，大多数情况下仅仅指感性意识中的三维空间形状的对称。
对称，确实在某种程度上支配了我们的审美观。比如，你觉得图 6.2中的图形哪个看上去更美？
那究竟什么是对称呢？我们可以用一句话简要概括：如果我们对一个事物做了某种操作之后，它看上去和先前是一样的，那它就是对称的。
上面这个定义中的“某种操作”很耐人寻味。比如，我们常常讲的三种对称类型：轴对称、旋转对称和中心对称，就可以通过赋予这个“操作”某种特定含义而得到。
轴对称：将物体沿着某一根轴进行翻转后与原物体重合。旋转对称：将物体绕着某个中心点旋转一定的角度（小于 360°）后与原物体重合。
中心对称：将物体绕着某个中心点旋转 180° 后与原物体重合，这也是旋转对称的特例。
受对称美的影响，人类在设计各种标识、服饰和建筑时，以及在摄影中，都融入了对称的理念（图 6.3）。
中国的汉字也包含着许多对称性，比如山、日、昍、王、非、干、中、串、叵等字是轴对称的汉字，而“互”则是中心对称的汉字。
除了形状的对称，我国古代的诗词和对联非常讲究“对仗”，这是一种文字语意和意境上的对称。比如，下面的这些古诗词名句，无一不体现了对称美。
大漠孤烟直，
长河落日圆。
——王维，《使至塞上》
无边落木萧萧下，
不尽长江滚滚来。
——杜甫，《登高》
露从今夜白，
月是故乡明。
——杜甫，《月夜忆舍弟》
乱花渐欲迷人眼，
浅草才能没马蹄。
——白居易，《钱塘湖春行》
人有悲欢离合，
月有阴晴圆缺。
——苏轼，《水调歌头·明月几时有》
无可奈何花落去，
似曾相识燕归来。
——晏殊，《浣溪沙》
除了对仗，古诗词中还有两种别样的对称：回文诗和宝塔诗。
春闺
[ 清 ] 李旸
垂帘画阁画帘垂，谁系怀思怀系谁？
影弄花枝花弄影，丝牵柳线柳牵丝。
脸波横泪横波脸，眉黛浓愁浓黛眉。
永夜寒灯寒夜永，期归梦还梦归期。
上面这首诗的每一句都是回文，也是一种文字的对称。而下面这首宝塔诗，则体现了形状的对称。
茶
[ 唐 ] 元稹
茶。
香叶，嫩芽。
慕诗客，爱僧家。
碾雕白玉，罗织红纱。
铫煎黄蕊色，碗转麹 A 尘花。
夜后邀陪明月，晨前命对朝霞。
洗尽古今人不倦，将知醉后岂堪夸。
但是，大自然中的对称远不止此。对称中存在着某种“重复”“均衡”“有序”的东西。科学美中的对称美源于自然界物质的形态美，及其运动图景所具有的广泛对称美，而数学与物理学中的对称美既有物理现象的对称美，也有公式的对称美。如果没有对称的思想，是很难欣赏这种理性美的。下面我们就来欣赏几个数学中的对称美。
下面的数组成了一个金字塔，被称为杨辉三角形（西方称之为“帕斯卡三角形”）。从第二行开始，每个数都是它上一行左边与右边的两个数之和（如果没有左边或右边的数，则视为 0），比如第六行左起的第三个数为 10，等于第五行左起第二个数 4 和第三个数 6 之和。可以看到，杨辉三角形呈现出左右对称的特点，它体现了数学中的二项式 (x + y)n展开式中系数的对称美。
对称性可以帮助我们避免可能出现的错误。比如，很多人一开始记不住
的展开式，如果我们有那么一点对称思维，就会发现，把 a 和 b 交换一下，那得到的依旧是
，也就是说，这个式子的展开式一定关于 a, b 对称。如果在展开后的表达式中将 a, b 交换后结果不相同，那一定是展开错了。
图 6.4 中的三阶幻方，为什么中间一定要填 5 ？除了用整体思维证明之外，我们也可以利用对称的思想分析：因为 5 是 1~9 这 9 个数字中最中间的一个，所以它理应位居幻方的中央。基于对称思维的这种直觉正是许多科学家用于探索未知的思维方式之一。
利用问题本身具有的对称性，可以降低许多问题的复杂度。我们先看一个可以直观地利用对称性降低问题复杂度的例子。
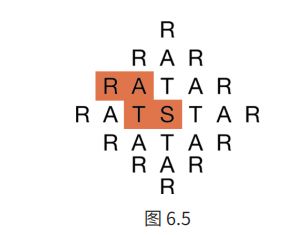
图 6.5 的字母排列图中，从中间的 S 开始，每次只能向上、下、左、右的相邻字母移动，不能沿对角线移动（图中给出了一种移动方法）。请问：一共有多少种方法可以拼出单词 STAR ？
我们一眼就注意到，这个图形上、下、左、右完全对称，因此只需要计算从 S 向某个方向出发可以有多少种方法得到 STAR 即可。比如，从 S 向上出发到达 T，之后从 T 出发可以到达 3 个 A；左边的 A 和右边的 A 是对称的，各有两种方法最后到达 R；上面的 A 与左右两个 A 不对称，有 3 种方法到达 R。因此，经过 S 上面的 T 一共有 7 种方法可以得出 STAR。根据对称性，一共就有 7×4=28 种方法。
这个问题也可以反过来思考，即从 R 开始。根据对称性，这个图形中的 R 可以分为两类：上、下、左、右 4 个顶点处的 R 为一类，另外四条边中间的 8 个 R 为另一类。从第一类的 R 到 S 只有一条路径，而从第二类的 R 到 S 有 3 条路径，因此一共有 4+8×3=28 种方法。
我们再考虑一个对称性不那么明显的计数问题：用 1, 1, 2, 2, 3 这五张卡片可以摆出多少个不同的五位数？
如果我们按照一开始的表述把“某种操作”定义为将 1 和 2 交换，那么得到的依然是 1, 1, 2, 2, 3 这五张卡片。这表明问题本身具有对称性。因此，如果我们采用最原始的枚举法，那显然，以 1 开头的五位数个数和以2 开头的五位数的个数相同。而如果把 1 和 3 变换一下，即将 1 换成 3，将 3 换成 1，那得到的是 3, 3, 2, 2, 1，这与原来的五张卡片不再相同，也就是说 1 和 3 在问题中不具备对称性。
最后来看一个稍微复杂一点儿的问题，这个问题完美地展示了对称思维的威力。
有 1、2、3 一直到 10 这 10 个数，将它们进行排列后，如果前一个数小于后一个数，那就让总和增加 1，请问：如果对所有的排列情况进行这样的计数，那么总和是多少？
我们当然可以先一个个地进行尝试，比如从小规模开始，然后尝试归纳。如果把 n 个数的排列情况总和记作 f(n)，那通过枚举不难发现：
仅仅根据这三个样本很难做出正确的归纳，很多人会觉得 f(5)=216，但事实上 f(5)=240!。可见，要正确枚举出 f(5) 的值需要非凡的耐力。而且，即便花了半天时间正确枚举出 f(5)=240，要想归纳出一般性的通项式也不容易。
但是，如果能利用问题本身具有的对称性，就能化繁为简。我们注意到，在所有的排列中，前一个数大于后一个数与前一个数小于后一个数的情况应该是对称的。所有的排列有 10! 种，每一个排列出现了 9 对相邻数，因此所有的排列一共包含 9×10! 对相邻数。根据对称性就容易得出，满足要求的总和是
一般性地，
相比于枚举，对称思维的威力显露无遗。大道至简，越是基本的数学定理，越是美妙。在数学上，就有这么一个美妙的与对称密切相关的基本原理：对偶原理。
对偶原理最早出现在射影几何的研究领域。在射影平面中，把一个定理的“点”和“直线”互换，然后其相对应的性质也替换后，得到的命题依然成立（图 6.6）
除了几何学，对偶原理在很多领域都有体现。在逻辑学、集合论中，被广泛使用的德摩根定律就以对偶的形式出现。在线性代数里，每个线性规划问题（称为原始问题）也有一个与它对应的对偶线性规划问题（称为对偶问题）。
这个世界的很多现象是对称统一的，比如物理学中的力与反作用力、动量守恒等。对称性往往可以指导我们做出新的发现。一个典型的例子是“电可以生磁，磁可以生电”，在对称思想的指引下，法拉第经过十几年的不懈努力终于实现了“磁生电”的梦想。
可以这么说，在大自然中，对称体现了一种平衡（图 6.7）。
有一个小游戏很能体现什么是平衡，有兴趣的读者不妨一试。
甲、乙两人玩如图 6.8 所示的红黑棋。在下棋时，每人每次只能走任意一枚棋子，每枚棋子可以走一格或几格，红棋从左向右走，黑棋从右向左走，但不能跳过对方的棋子走，也不能叠放在对方有棋子的格子中，一直到谁无法走棋时，谁就失败。如果按照甲先乙后的顺序走棋，你若想取胜，愿意当甲还是当乙？有什么必胜策略？
推荐阅读
作者：昍爸、昍妈
数学之美是什么？数学之美在哪里？学会欣赏数学的美，才能真正理解数学
展现数学均衡有序的思维之美、简洁精确的逻辑之美、度量万物的直观之美、探索奥秘的创造之美
