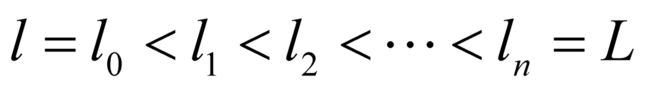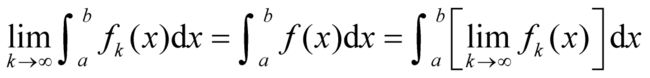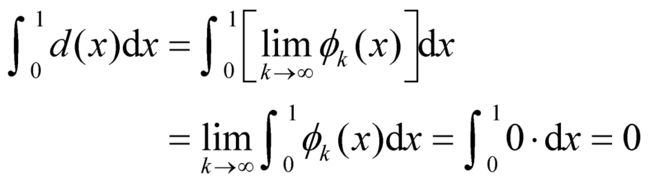历经两个世纪，微积分最终在他的手中得以完善！

随着20世纪的到来，数学家们有理由为自己喝彩。微积分已经存在了两个多世纪。它的基础已经不容置疑，许多悬而未决的问题已经宣告解决。自从牛顿和莱布尼茨初创微积分以来，分析学走过了漫长的路程。

适逢其时，亨利·勒贝格卷入到这门学科中来。他在1902年对积分论进行了革命，并且进一步把这场革命推进到实分析，那时他还是巴黎大学的一名才华横溢的博士生。他以一篇博士论文实现了这一目标，那篇论文被描述成“以往所有数学家写就的最佳论文之一”

勒贝格利用可测集和可测函数的思想作出他的最大贡献：勒贝格积分。

有界函数f的黎曼积分从把定义域剖分为细小的子区间的一个划分开始，在这些子区间上构建矩形，它们的高由函数值确定，最后令最大子区间的宽度收缩为零。相反，替代的勒贝格积分乃是基于一种简单而又富有想象力的思想：采用函数值域的划分代替定义域的划分。

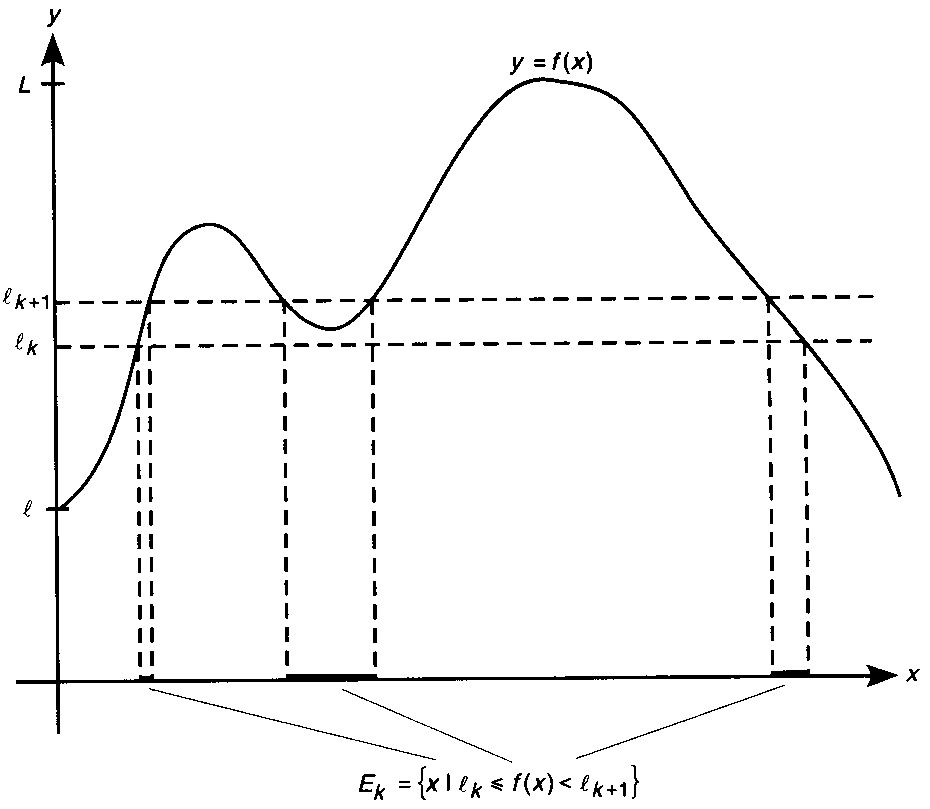
我们用图解来说明，考虑图14-3中的有界可测函数。勒贝格令为f在区间[a, b]上的下确界和上确界，即函数的最大下界和最小上界，所以区间[l, L]包含函数的值域。于是，对于任意，勒贝格设想区间[l, L]的一个由点

构成的划分，其中相邻分点之间的最大间隔小于ε。

图　14-3

用沿y轴的这样一个划分，我们建立“勒贝格和”。像黎曼和一样，我们将用面积已知的一些区域逼近曲线下方的区域，不过我们可以不再要求这些区域一定为矩形。相反，我们考虑沿y轴的子区间，并且注意由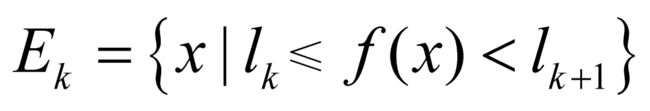定义的[a, b]的子集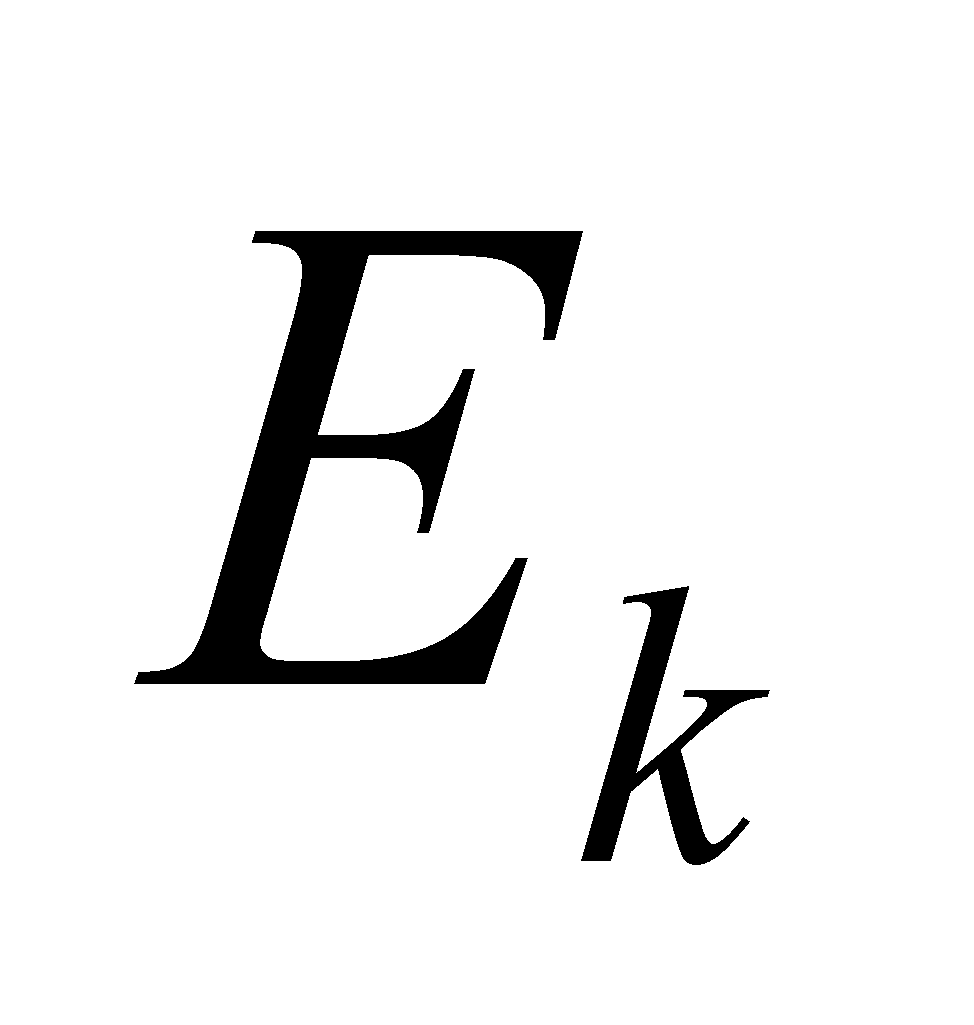。这个子集就是图14-3中在x轴上标示出的部分。这里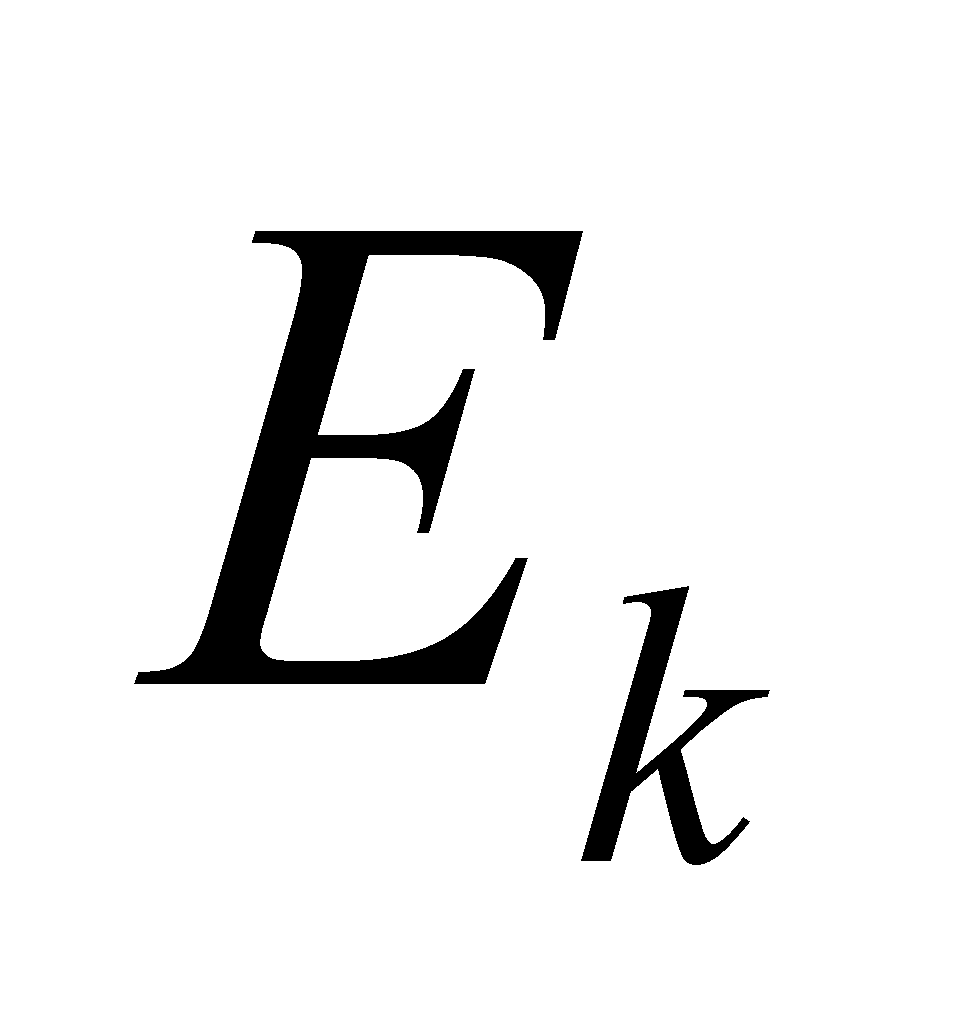，是三个子区间的并集，但是它的结构可能非常复杂，这同求积分的函数有关。

在黎曼方法的相似步骤中，我们是构造一个矩形，它的高是函数值的近似值，宽是相应子区间的长度，而其面积为这两个值的乘积。对于勒贝格积分，我们用作为函数在集合上的近似值，但是如果不是区间的情形，如何去确定它的长度呢？

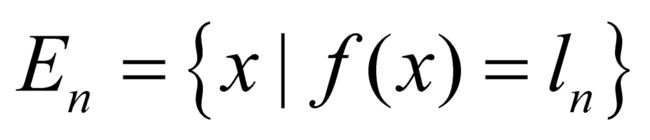毫不奇怪，答案是用集合的测度扮演这种长度的角色。我们用高乘“长度”得到的作为黎曼和中窄小矩形之一的相应面积。在函数值域的所有子区间上对这些面积求和，我们得到一个勒贝格和，在这个级数中我们令最后一项为。最后，勒贝格令，致使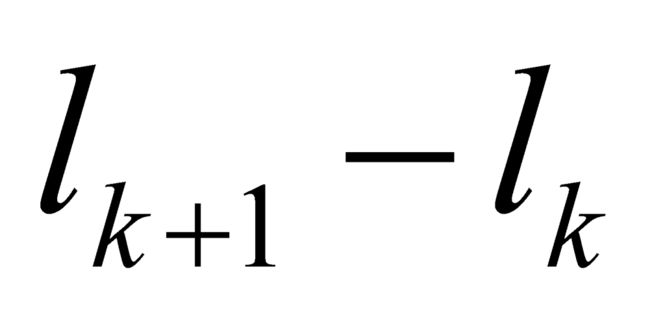的最大值也趋近零。如果通过极限过程产生一个唯一的值，我们就说f在[a, b]上是勒贝格可积的，并且定义

在继续进行讨论之前，我们必须说明两个问题。第一，很明显，集合把区间[a, b]划分成若干子集，不过不一定是子区间。第二，我们假定f是可测的，根据式（4），这个假定蕴含每个以及是可测集，所以我们完全可以讨论关于的问题。至此，一切都井然有序。

勒贝格在为一般读者编写的一本书中，用一个比喻来对比黎曼的方法与他自己的方法。他想象一位零售商，在一天终结时想要汇总营业收入。对于这位店主来说，一种选择是“按照随机顺序计算到手的现金和账单”。勒贝格把这样一位零售商称为“缺乏系统观点的”人，他依次累加收集起来的款项：1美元，10美分，25美分，另1美元，10美分，如此等等。这种方法犹如当他们从左至右越过区间[a, b]时提取遇到的函数值。对于黎曼积分，这个过程是由定义域中的值“驱动”的，而值域中的值被搁置一旁。

勒贝格接着指出，如果不这样做，店主在结账时不考虑收到每笔款项的顺序，而代之以按款项的面值分组，难道不是更为可取吗？例如，可能共计收到10美分12笔，25美分30笔，1美元50笔，等等。这样，计算一天的收入将变得很简单：用每种币值的数量（对应于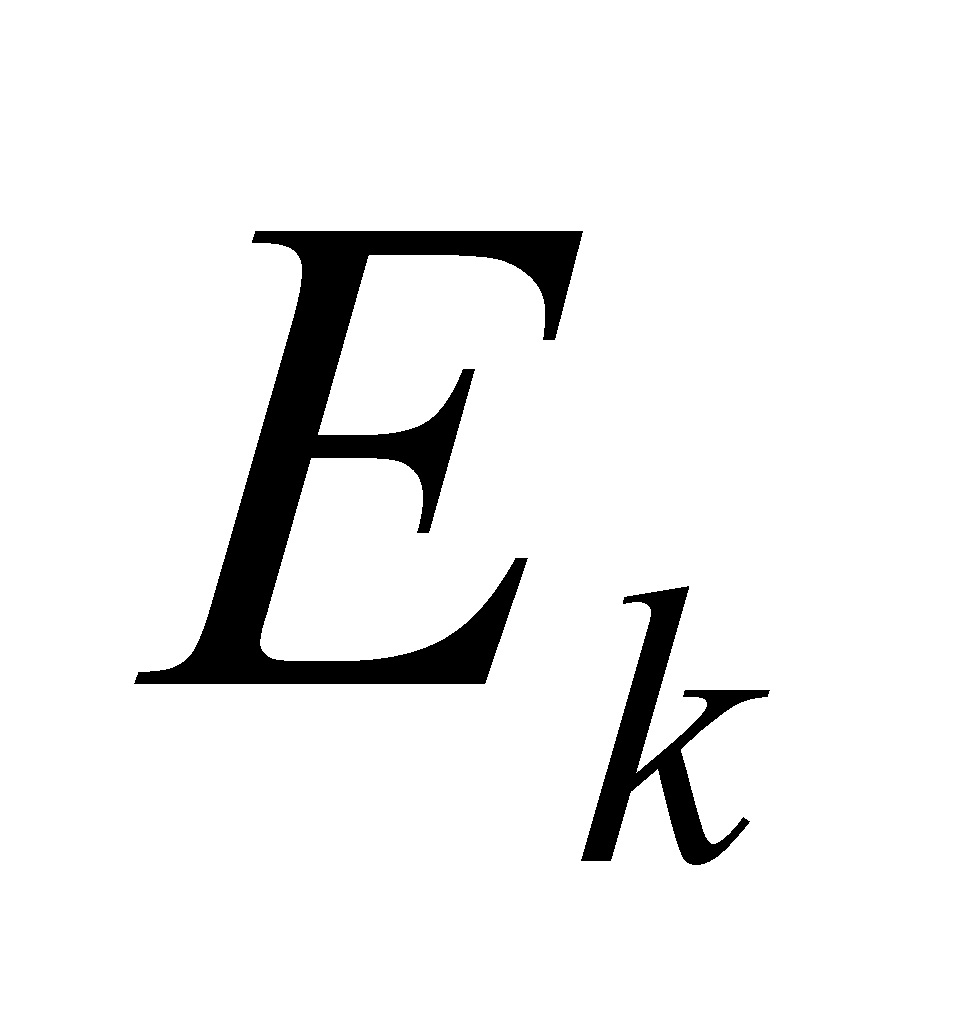的测度）乘以币值（对应于函数值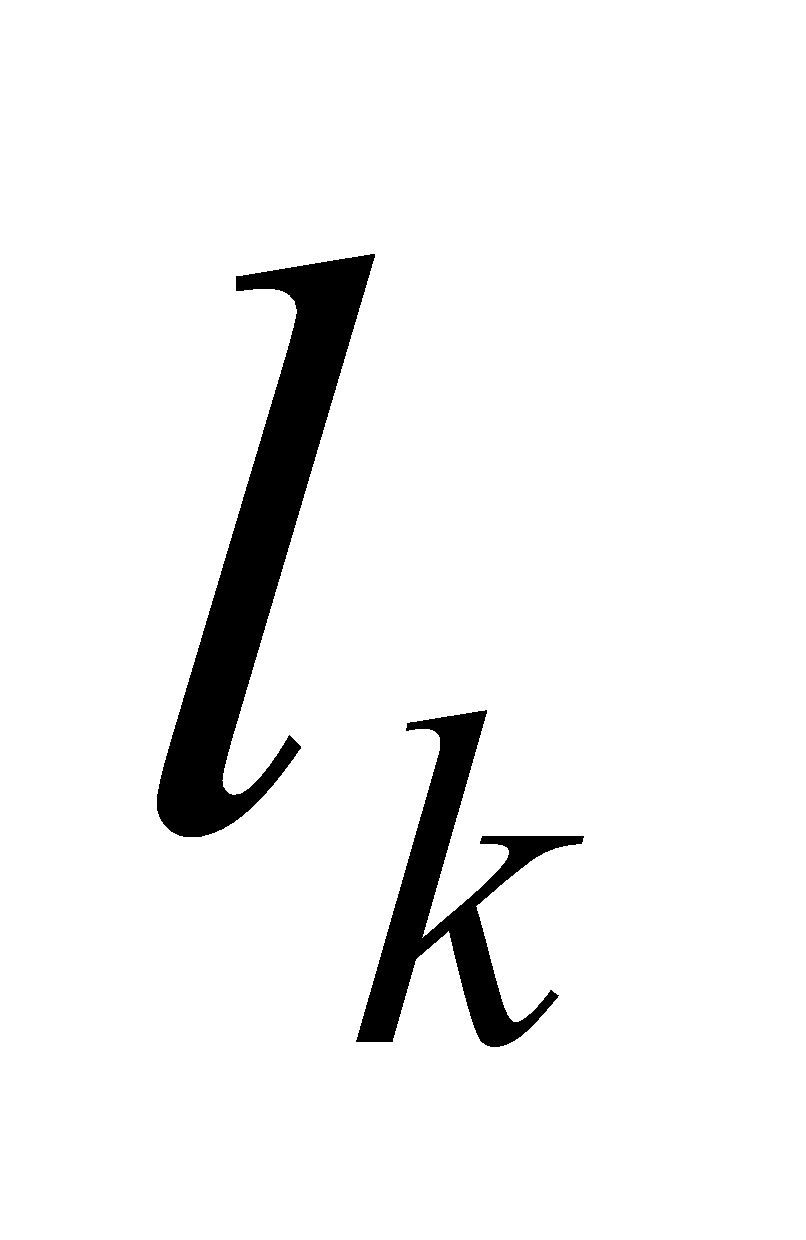），然后对结果求和。这种情况下，正如勒贝格积分的情形，其过程是由值域中的函数值驱动的，而划分定义域的被搁置一旁。

勒贝格承认，对于商业经营中涉及的有限的量，这两种方法产生同样的结果。“但是对于我们必须求数目无限的极微小的量之和而言，”他写道，“这两种方法之间存在着巨大差别。”为了强调这种差别，他指出：

我们的积分的构造定义，同黎曼积分的定义十分相似。不过，黎曼是把变量x改变的区间剖分成微小的子区间，而我们则是剖分函数f?(x)改变的区间。

为了说明自己并非漫无目标地追求定义，勒贝格证明了关于他的新积分的若干定理。我们将考察其中几个定理，但是不予证明。

定理 1　地如果f(x)是区间[a, b]上的有界黎曼可积函数，那么f是勒贝格可积的，并且在两种情况下具有相同的积分值。

这个结果是令人欣慰的，因为它说明勒贝格积分保存了黎曼积分的精华。

定理 2　如果f(x)是区间[a, b]上的有界可测函数，那么它的勒贝格积分存在。

我们从这个定理看出勒贝格思想的巨大力量，因为可测函数族包含的函数远远多于黎曼可积函数（即所有那些几乎处处连续的函数）族。简而言之，勒贝格可积的函数多于黎曼可积的函数。定理1和定理2表明，勒贝格名副其实地扩充了过去的理论。

例如，我们已经知道狄利克雷函数d(x)在区间[0, 1]上是有界的和可测的。因此，尽管事实上积分在黎曼的理论下是没有意义的，然而作为勒贝格积分却是存在的。

更为可取之处在于，这个积分值是很容易计算的。我们从值域的任意划分着手。根据狄利克雷函数的性质，

对于这个随意的划分，勒贝格和为

正是由于对于任意划分这个勒贝格和为零，所以，所有这样的极限也为零。也就是说，。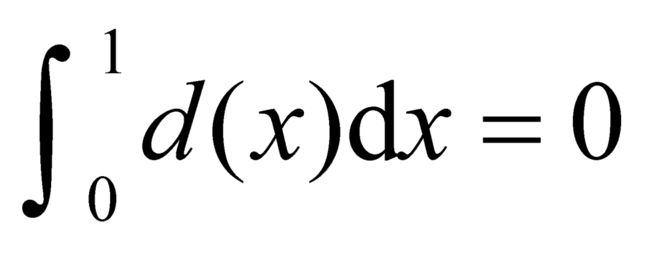

狄利克雷函数是处处不连续的这一事实，使它成为黎曼不可积的，但是这样普遍的不连续性对于勒贝格积分是无关紧要的。这种结果无可争辩地说明数学上取得的巨大进展。

定理 3　地如果f和g是区间[a, b]上的有界可测函数，并且几乎处处有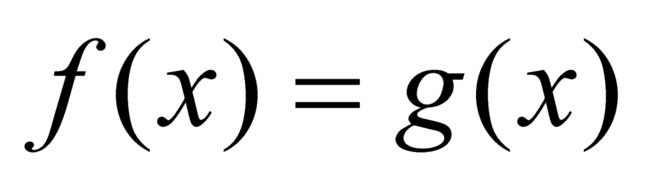，那么。

这个定理说明，改变一个可测函数在一个测度为零的集合上的值，对于它的勒贝格积分的值没有影响。对于黎曼积分，如果改变函数在有限个点上的值，不会改变积分值，但是一旦胡乱修改无穷多点上的函数值，结果就无法预料了。相形之下，勒贝格积分具备足够的抗变能力，我们可以在一个测度为零的无穷集合上改变函数值而不影响它的可积性和积分值。

为了考查这个定理的作用，我们重温区间[0, 1]上的狄利克雷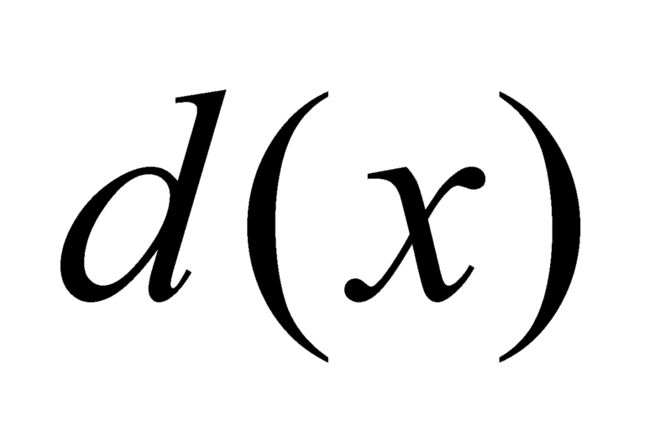函数和直尺函数，并且通过引进在[0, 1]上所有点都等于0的函数，组成一个三位一体的函数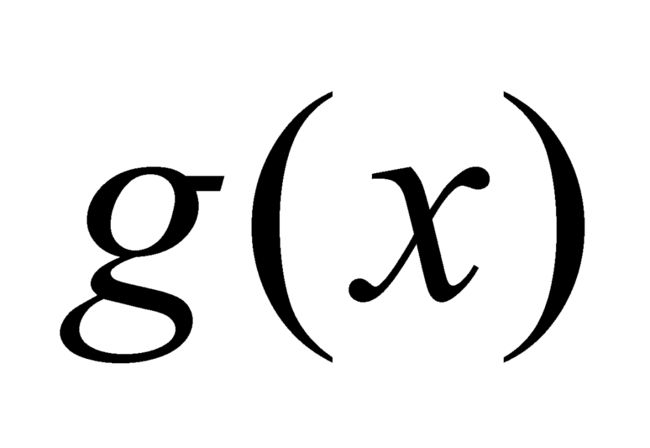。这三个函数d, R, g自然不是全等的，因为它们在单位区间的有理数点上具有不同的值。但是从测度理论的观点看，这样的差别是微不足道的，因为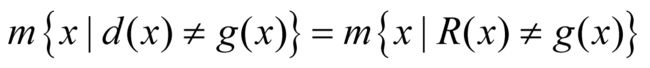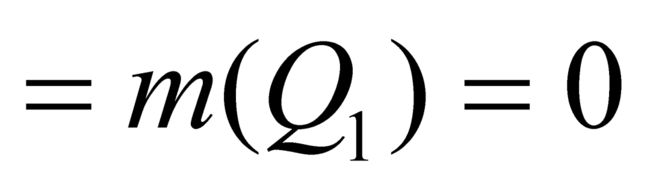。换句话说，狄利克雷函数和直尺函数几乎处处等于零。由定理3推出，这正是我们过去见过的结果。

在勒贝格的论文中还有另外一个重要定理，那就是我们现在所说的有界收敛定理。他在非常弱的条件下，证明了这个允许进行极限与积分的交换的定理。这是超越黎曼理论的一项重大进展。

定理4（勒贝格有界收敛定理）　如果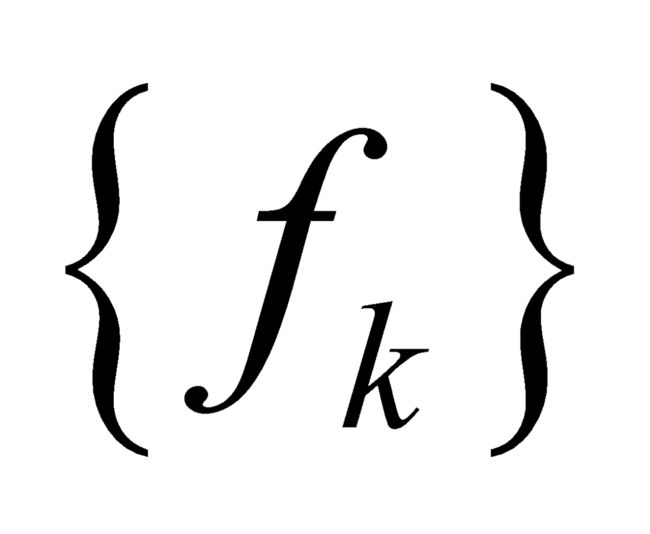是区间[a, b]上的可测函数序列，其中的函数以数M >0一致为界（即对于所有k≥1和[a, b]内的所有x有），并且如果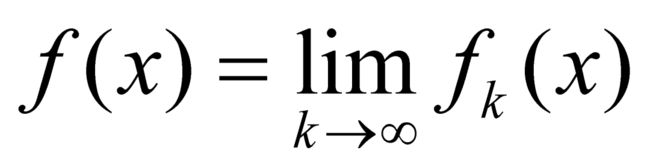是点态极限，那么

利用这个定理我们可以提出对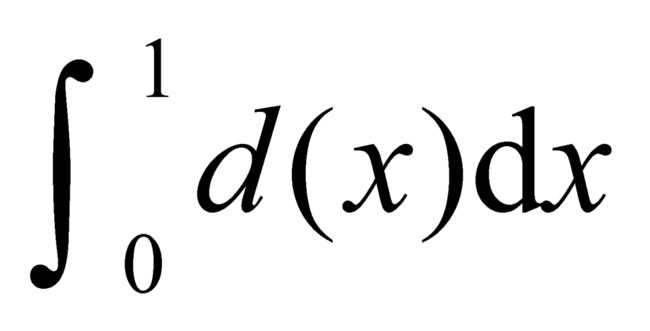的第三次处理。早先我们引进了区间[0, 1]上的一个函数序列，如在式（1）中所见，对于这个序列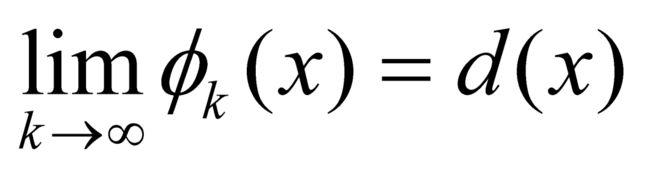，。显然，对于所有x和全部k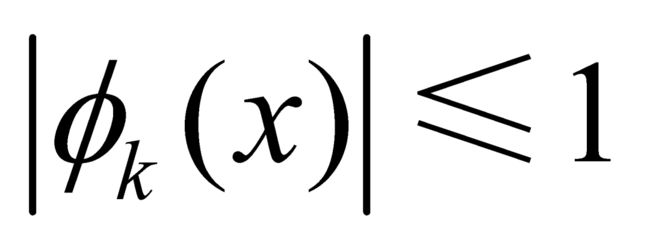，，所以这是一个一致有界的函数族，同时由于每个在除k个点之外为零，可知每个函数是可测的并且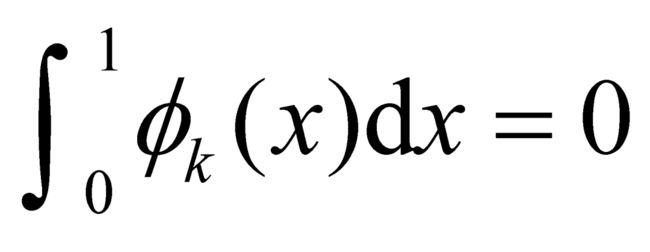。根据勒贝格有界收敛定理，我们再一次推出

勒贝格有界收敛定理的证明（1904）

时代铸就一个人的最后成就。我们回忆一下，沃尔泰拉曾经发现一个病态函数，它具有有界而不可积的导数。在沃尔泰拉时代， “不可积的”自然是指“不是黎曼可积的”。

然而，采用勒贝格定义的替代积分，这个函数的病态特征随之消失。因为倘若F是具有有界导数F'的可微函数，那么勒贝格积分必定存在，这正如我们在第13章所见，F'是属于贝尔0类或贝尔1类的函数。这是使其成为勒贝格可积的充分条件。

有界收敛定理更值得称道之处还在于，它使勒贝格得以证明下面的定理。

定理 5　如果函数F在区间[a, b]上是可微的并且具有有界的导数F'，那么。

这是完全恢复原来的完美形态的微积分基本定理。对于勒贝格积分，为使基本定理成立，对导数无需附加限制条件，例如不必要求导数是连续的。因此，在一定的意义下，勒贝格把微积分中的这个处在中心地位的结果恢复成它在牛顿和莱布尼茨时代那种“自然的”形式。

在行将结束之际，我得承认，许许多多的技术细节在对勒贝格工作的这个简短介绍中无法顾及。对他的思想的全面论述需要花费大量的时间和篇幅，那样自然会使那些来自他的博士论文的思想越发令人惊叹！毫不奇怪，这篇学位论文出类拔萃，独树一帜。

在1904年那本重要的专题著作的序言中，勒贝格承认他的那些定理把我们从“优美的”函数之邦带到一个更复杂的函数王国，而为了解决那些简单陈述的具有历史意义的问题，还需要在这片王国居住下来。他写道：“这是为了解决已经提出的那些问题而不是出于对复杂事物的偏爱，我在书中引进一个积分定义，这个定义比黎曼积分的定义更具有普遍性，并且把黎曼积分作为一个特例。” 

为的是解决历史留下的问题而不是为了使生活变得错综复杂化：这是亨利·勒贝格在他研究数学的旅程中所奉行的金科玉律。

  推荐阅读

作者：[美] William Dunham

译者：李伯民 汪军 张怀勇

第七届文津图书奖推荐书目

这不是一本数学家的传记，而是一座展示微积分宏伟画卷的陈列室

汇聚了牛顿、莱布尼茨、伯努利兄弟、欧拉、柯西、黎曼等耳熟能详的数学大师经典卓著