JAX-FLUIDS：可压缩两相流的完全可微高阶计算流体动力学求解器

原文来自微信公众号“编程语言Lab”：论文精读 | JAX-FLUIDS：可压缩两相流的完全可微高阶计算流体动力学求解器
搜索关注“编程语言Lab”公众号（HW-PLLab）获取更多技术内容！
欢迎加入 编程语言社区 SIG-可微编程 参与交流讨论（加入方式：添加小助手微信 pl_lab_001，备注“加入SIG-可微编程”）。

翻译 | 瞿家港 (哈工大流体力学博士研究生)，沈明 (编程语言实验室研究员)
校对 | 海丽娟
编辑 | Hana

华为编程语言实验室从编程语言的角度面向 AI + 科学计算 进行探索研究，致力于提供更适合 AI 与科学计算融合应用开发的编程技术方案。来自慕尼黑工业大学 Adams 教授的这篇论文是最新在 CFD+ML 方向看到的比较有意思的研究工作，特此分享出来以飨读者。

论文信息

Jax-fluids: A fully-differentiable high-order computational fluid dynamics solver for compressible two-phase flows. Deniz A. Bezgin, Aaron B. Buhendwa, and Nikolaus A. Adams. 3 2022.

论文地址：https://arxiv.org/abs/2203.13760

Github：https://github.com/tumaer/JAXFLUIDS

译者注

传统的计算流体力学 (后简称 CFD)，其求解过程完全采用数值微分进行计算，参数空间完全不可微。基于机器学习的计算流体力学应用 (后简称 ML-CFD)，常常构建 ML 模型来代替 CFD 的部分功能/模块，从而得到更优的计算结果，这种情况下的 ML 模型则是可微的。

多数 ML-CFD 的应用是采用离线训练的，即，先使用传统 CFD 求解器得到训练数据，再将之导入到 ML 框架中进行训练，最后将训练好的模型耦合到传统的 CFD 求解器中。这样的流程十分繁琐，且属于完全数据驱动，与偏微分方程 (后简称 PDE) 的动力学性质无关。

如果能构建这样一个计算框架，使得 CFD 求解过程和 ML 的训练/推理过程完全融合，即能在训练过程中得到来自 CFD 求解实时的反馈，可以更有效地学习到符合该 PDE 动力学特征的模型。而且，这将使得 CFD 和 ML 模型的开发更加方便和快捷。

JAX ¹ 为我们实现这样的构想提供了方便的平台，能方便地编写 CFD 求解器，也能在 GPU 平台并行，还能提供自动微分功能，从而实现 ML 模型的训练。

相关推荐

SIG-可微编程

能微分会加速的 NumPy —— JAX

浅谈 eDSL 在科学计算和数据分析领域的发展趋势

从自动微分到可微编程语言设计 (一）（二）（三）

# 摘要 #

背景

物理系统有偏微分方程 (PDEs) 控制，其中 Navier-Stokes 方程 ² 为描述流体流动的 PDEs，代表着具有复杂时空相互作用的非线性物理系统。PDEs 通常使用 数值方法 (数值离散-迭代求解) 进行求解，近些年机器学习 (ML) 方法为求解 PDEs 提供了一个新途径，ML 在计算流体力学 (CFD) 领域中的应用也越来越多。

动机

当前，没有一个通用的 ML-CFD 软件包可以提供以下功能：

• 提供最新的求解 CFD 的数值方法
• 提供 ML 和 CFD 之间无缝衔接
• 自动微分 (AD) 功能 (AD 提供的梯度信息能够优化 CFD 模型，因此 AD 对 ML-CFD 的研究至关重要)

提出

JAX-FLUIDS，可压缩两相流的完全可微高阶计算流体动力学 Python 求解器，可以：

• 模拟三维湍流、可压缩流动、两相流等复杂流体问题；
• 完全采用 JAX 编写，因此可以将现有的 ML 模型耦合到 CFD 求解器中；
• 支持端到端的优化，ML 模型可以使用 CFD 求解器求解过程中的梯度信息，因此 ML 模型不仅可以使用 PDE 包含的信息，还可以使用所应用的数值方法的信息。

译者注：端到端是一种解决问题的思路，与之对应的是多步骤解决问题，也就是将一个问题拆分为多个步骤分步解决，而端到端是由输入端的数据直接得到输出端的结果。

# 引言 #

经典的 CFD 方法和 ML 方法的融合需要强大的新方法达成以下目标：

• 允许数据驱动模型与 CFD 方法的无缝集成
• 整个算法 (CFD&ML) 实现端到端的自动微分

本文讨论了混合 ML 加速的 CFD 求解器所面临的挑战，并强调了如 JAX-FLUIDS 这样的新软件架构如何促进 ML-CFD 的研究。

上世纪开始，CPU 快速发展为 CFD 的发展奠定了基础，CFD 逐渐发展成为一个独立的科研研究领域。近些年来机器学习为物理科学的发展注入了新的活力，强大的自动微分框架如 TensorFlow、PyTorch 和 JAX 推动了 ML 方法在自然科学和工程科学中的发展。例如采用 ML 方法从数据发现 PDE、物理信息神经网络 (PINNs) 求解反问题等。

流体力学是一个数据丰富、计算密集的科学，这是由于 Navier-Stokes 方程的高度复杂的时空非线性本质决定的，例如湍流表现出强间歇性和非高斯性的混沌行为特征。机器学习提供了一系列新的数据驱动方法来解决流体力学中一些长期存在的问题。

用于科学计算的 ML 方法能以不同的依据进行分类：

• 按模型和训练中包含的物理先验知识的水平进行分类
  完全数据驱动模型的优点在于：实现简单、推理效率高；缺点在于：收敛性、泛化性和稳定性等不能保证，难以实施物理约束等。而经典数值方法则能保证物理约束，如今结合 ML 和经典数值方法的研究越来越多。
• 在线训练/离线训练
  目前大多 ML 模型都是离线优化的，既在 ML 模型训练完成之后，再安插到传统 CFD 软件中，用于评估下游的计算任务。

尽管离线训练相对容易，但这种方法仍存在一些缺点：

• 这些模型在训练和测试时面对的数据分布不匹配；
• 它们通常不会直接学习 PDE 的动力学先验知识；
• 流体力学求解器通常非常复杂，使用 Fortran 或 C++ 等编程语言编写，并针对 CPU 计算进行了大量优化，这与 ML 研究的一般过程相反，ML 模型通常使用 Python 进行训练，并针对 GPU 的使用进行优化。将这些 ML 模型插入到现有的 CFD 软件框架中会比较麻烦。

为了解决这些问题，研究者们开始研究直接使用 Python 编写可微分的 CFD 求解器框架，从而可以进行端到端的训练 ML 模型。ML 模型在端到端的训练过程中，可以在训练过程中感受到动态的 PDE 求解过程，并实时地看到自己的输出。目前已有的可微分科学计算框架有：

• PhiFlow ³，TUM，兼容 JAX、PyTorch、TensorFlow、Numpy，为优化和机器学习应用程序构建的开源仿真工具包。
• JAX-CFD ⁴，Google，CFD 求解器 (尚不完善，如仅支持周期性边界)，支持：
  • 空间离散支持有限体积、有限差分和谱方法
  • 时间离散：一阶格式
  • 压力求解器：共轭梯度、实 FFTs 进行快速对角化
  • 仅支持周期性边界
  • 对流：二阶 Van-Leer 格式
  • Smagorinsky 涡粘性模型
• JAX-MD ⁵，Google，端到端的分子动力学求解器。

机器学习在计算流体力学以及更广泛的计算物理领域的稳步崛起和成功需要新一代算法，这些算法允许：

• 高级编程语言的快速原型设计
• 在 CPU、GPU 和 TPU 上运行
• 将机器学习模型无缝地集成到求解器框架中
• 对数据驱动模型进行端到端优化的完全可微算法

# 物理模型 #

译者注：本节介绍了描述流体运动的控制方程 (动量方程、连续性方程、能量方程)，即描述无粘流体运动的 Euler 方程和粘性流体运动的 Navier-Stokes 方程。在 CFD 的编程范式中，尤其在有限体积法的计算程序中，习惯将微分方程写成具备统一形式的通量表示形式，如下文所介绍。

本文将关注 无粘流体的可压缩 Euler 方程，和 粘性流体的可压缩 Navier-Stokes 方程。

定义以下基本变量：处于位置 $\mathbf{X}=[x,y,z{]}^T=[x_1,x_2,x_4{]}^T$ 及时间 $t$ 的流体状态采用矢量 $\mathbf{W}=[\rho ,u,v,w,p{]}^T$ 表示。这里，

• $\rho$ 为密度
• $\mathbf{u}=[u,v,w{]}^T=[u_1,u_2,u_3{]}^T$ 为速度矢量
• $p$ 为压力

由于本文关注 可压缩流体，因此，采用 守恒变量 描述问题更加合理，即，

$$\mathbf{U}=[\rho ,\rho u,\rho v,\rho w,E{]}^T$$

其中，

• $\rho \mathbf{u}=[\rho u,\rho v,\rho w{]}^T$ 是三个空间维度上的动量
• $E=\rho e+\frac{1}{2}\rho \mathbf{u}\cdot \mathbf{u}$ 是单位体积的总能量
• $e$ 是单位质量下的内能

将可压缩 Euler 方程写成 $\mathbf{U}$ 的微分方程，

$$\frac{\partial \mathbf{U}}{\partial t}+\frac{\partial \mathbf{F}(U)}{\partial x}+\frac{\partial \mathbf{G}(U)}{\partial y}+\frac{\partial \mathbf{H}(U)}{\partial z}=0$$

其中通量 $\bm F,\bm G,\bm H $ 定义为，

F = ( ρ u ρ u 2 + p ρ u v ρ u w u ( E + p ) ) , G = ( ρ v ρ v u ρ v 2 + p ρ v w v ( E + p ) ) , H = ( ρ w ρ w u ρ w v ρ w 2 + p w ( E + p ) ) \bm F = \begin{pmatrix} \rho u \\ \rho u^2+p \\ \rho uv \\ \rho uw \\ u(E+p) \end{pmatrix}, \bm G = \begin{pmatrix} \rho v \\ \rho vu \\ \rho v^2+p \\ \rho vw \\ v(E+p) \end{pmatrix}, \bm H = \begin{pmatrix} \rho w \\ \rho wu \\ \rho wv \\ \rho w^2+p \\ w(E+p) \end{pmatrix} F= ​ρuρu2+pρuvρuwu(E+p)​ ​,G= ​ρvρvuρv2+pρvwv(E+p)​ ​,H= ​ρwρwuρwvρw2+pw(E+p)​ ​

可压缩 Navier-Stokes 方程也写成通量的形式：

$$\frac{\partial \mathbf{U}}{\partial t}+\frac{\partial \mathbf{F}(U)}{\partial x}+\frac{\partial \mathbf{G}(U)}{\partial y}+\frac{\partial \mathbf{H}(U)}{\partial z}=\frac{\partial {\mathbf{F}}^{\mathbf{d}}(U)}{\partial x}+\frac{\partial {\mathbf{G}}^d(U)}{\partial y}+\frac{\partial {\mathbf{H}}^d(U)}{\partial z}+\mathbf{S}(U)$$

其中耗散通量 ${\mathbf{F}}^d,{\mathbf{G}}^d,{\mathbf{H}}^d$ 定义如下：

F = ( 0 τ 11 τ 12 τ 13 ∑ i u i τ 1 i − q 1 ) , G = ( 0 τ 21 τ 22 τ 23 ∑ i u i τ 2 i − q 2 ) , H = ( 0 τ 31 τ 32 τ 33 ∑ i u i τ 3 i − q 3 ) \bm F = \begin{pmatrix} 0 \\ \tau^{11} \\ \tau^{12} \\ \tau^{13} \\ \sum_i u_i\tau^{1i}-q_1 \end{pmatrix}, \bm G = \begin{pmatrix} 0 \\ \tau^{21} \\ \tau^{22} \\ \tau^{23} \\ \sum_i u_i\tau^{2i}-q_2 \end{pmatrix}, \bm H = \begin{pmatrix} 0 \\ \tau^{31} \\ \tau^{32} \\ \tau^{33} \\ \sum_i u_i\tau^{3i}-q_3 \end{pmatrix} F= ​0τ11τ12τ13∑i​ui​τ1i−q1​​ ​,G= ​0τ21τ22τ23∑i​ui​τ2i−q2​​ ​,H= ​0τ31τ32τ33∑i​ui​τ3i−q3​​ ​

应力张量 ${\tau }_{ij}$ 定义如下：

$${\tau }_{ij}=\mu \left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)-\frac{2}{3}\mu {\delta }_{ij}\frac{\partial u_k}{\partial x_k}$$

在本文的计算中，所有的物理量都采用相应的参考值进行无量纲化。

# 数值模型 #

译者注：JAX-FLUIDS 的 CFD 求解器是基于卡式坐标系的有限体积法 (FVM) 构建的，其数值原理上等价于有限差分法 (FDM)。原文中本节介绍了一般 FVM 的求解过程，译者以 FDM 为例，描述采用数值微分迭代求解微分方程的过程。

有限差分方法求解 PDE 的简单示例 扩散方程，

$$\begin{gathered} \frac{\partial T}{\partial t}=\alpha \frac{{\partial }^{2}T}{\partial x^2} \\ T(t=0,x)=\{\begin{array}{ll}T=50,& x=0\\ T=0,& x=L\\ T=20,& other\end{array} \\ T(t,x=0)=50,T(t,x=L)=0 \end{gathered}$$

上述方程组描述了温度扩散方程的控制方程、初始条件和边界条件。

有限差分方法求解的过程如下。

1. 空间计算域的离散 (建立求解网格)

方程的空间计算域为 $x\in [0,L]$，这里将该区域划分为若干个 ($N+1$) 均匀网格 (线段)，每个网格的长度为 $\Delta x=L/N$。

2. 时间离散

我们仅计算一段时间内的方程的演化轨迹，即 $t\in [0,t_{end}]$。同样地，假设间隔均匀，$t_{end}=M\Delta t$。

3. 方程的离散

采用数值微分重写扩散方程，

$$\begin{gathered} \frac{T_{j+1,i}-T_{j,i}}{\Delta t}=\alpha \frac{T_{j,i+1}-2T_{j,i}+T_{j,i-1}}{(\Delta x{)}^2} \\ {T}_{j+1,i}=\alpha \frac{T_{j,i+1}-2T_{j,i}+T_{j,i-1}}{(\Delta x{)}^2}\times \Delta t+T_{j,i} \end{gathered}$$

4. 迭代求解

可以通过上式，在已知初始条件 ($T(t=0,x)=T_{0,i}$) 以及边界条件 ($T(t,x=0),T(t,x=L)$) 的前提下，求解往后任意时刻下的温度。

译者注：
有限体积法（FVM）与有限差分法（FDM）类似，可以这样理解，FVM 计算结构单元的平均值，FDM 计算网格节点的值。
FVM 优势之一在于求解非结构化网格时的连续性强。本文却将计算域的离散局限在卡式坐标系中，这样做的考虑，译者推测，最重要的原因应该是为了妥协代码/算法复杂度。此外，本文创新点之一在于支持两相流的计算，因此选择了 FVM。

有限体积法

第 2 节 物理模型中介绍的是守恒律方程的微分形式，而本文采用 有限体积法 求解 Euler 方程和 Navier-Stokes 方程的 积分形式。

在卡式坐标系中，假设一系列立方体单元为最小求解单元 (cell)，即 $cell(i,j,k)$ 在空间维度 $x,y,z$ 上的长度为，

$$\Delta x,\Delta y,\Delta z$$

体积为，$$V=\Delta x\Delta y\Delta z$$

进一步地，可以假设，

$$\Delta x=\Delta y=\Delta z$$

在有限体积法中，计算单元内守恒变量的平均值定义为，

$${\bar{\mathbf{U}}}_{i,j,k}=\frac{1}{V}{\int }_{x_{i-\frac{1}{2},j,k}}^{x_{i+\frac{1}{2},j,k}}{\int }_{x_{i,j-\frac{1}{2},k}}^{x_{i,j+\frac{1}{2},k}}{\int }_{x_{i,j,k-\frac{1}{2}}}^{x_{i,j,k+\frac{1}{2}}}\mathbf{U}dxdydz$$

将体积积分带入到第 2 节的方程中，就可以得到计算单元 $cell(i,j,k)$ 均值的时空演化关系。

其他的计算细节见后续的介绍。

时间积分

采用 显式总变差递减 (TVD) 龙格库塔 (RK) 方法 进行时间离散，计算时间步的大小用 CFL 数进行控制。

通量的计算

对流通量采的计算支持常见的迎风格式，包括 通量差分分裂 (FDS，即高阶 Godunov 方法) 和 通量矢量分裂 (FVS)。耗散通量的计算支持二阶/四阶中心差分方法。

源项和力

源项 $\mathbf{S}(\mathbf{U})$ 表示体积力或热源，在计算一些经典湍流的案例中需要在 Navier-Stokes 方程中加入该项，如槽道湍流或受外力驱动的均匀各向同性湍流。

两相流的水平集方法

JAX-FLUIDS 的一大突出之处是 支持两相流的计算，该框架支持分离多相流模型 (水平集方法) 的计算接口。水平集方法的核心思想就是将界面看成高一维空间中某一函数，从而避免对两相交界面的曲线曲面参数化。

计算域和边界条件

JAX-FLUIDS 的计算域为 立方体样式，在每个边界处提供对称、周期性、无滑移 (支持指定避面速度为常数或函数)、Dirichlet、Neumann 边界条件。在二维的算例中，JAX-FLUIDS 还支持沿单个边界位置施加多种不同类型的边界条件。

Computational domain with boundary locations ## \# 软件实现细节 \#

以往，CFD 求解器大多是使用低级编程语言编写的，如 Fortran 和 C/C++ 等。这些语言能提供高计算性能和 CPU 并行能力。但是，这些编程语言不能快速方便地集成 ML 模型 (通常，这些 ML 模型使用 Python 编写)，也不具备自动微分的能力。

基于当前的需求，我们期望存在一个高性能的 CFD 框架，既能够无缝集成 ML 模型，同时实现端到端的优化功能。Google 开发的 Python 库 JAX 能够提供这些关键特性，所以我们选择基于 JAX 开发了 JAX-FLUIDS。

本章介绍 JAX-FLUIDS 中的实现细节和算法结构。

JAX 中的数组编程

JAX 是一个用于高性能计算的 Python 库，底层依赖 XLA 编译器将 Python 源码编译成能够在 CPU，GPU 和 TPU 上执行的高效代码。JAX 支持方便易用的自动微分。另外，JAX 参考 Python 中非常流行的 Numpy 库，提供了 JAX NumPy。可以说，JAX 等价于 Numpy + 自动微分 + 异构多硬件支持。

JAX Numpy 中，核心的数据对象是 高维数组 jax.numpy.DeviceArray。因此，JAX-FLUIDS 也使用数组存储所有的计算数据。

具体来说，守恒 (conservative) 变量 $\mathbf{U}$ 和原始 (primitive) 变量 $\mathbf{W}$，会被存储到一个 shape 为 $(5,N_x+2N_h,N_y+2N_h,N_z+2N_h)$ 的数组中。

其中，$(N_x,N_y,N_z)$ 代表三个空间方向上的有效网格数量，$N_h$ 代表边界过渡网格 (halo cells) 数。在 JAX-FLUIDS 实现中，可以很容易将三维的数组退化到二维或者一维的情况。

在数组编程范式中，每个操作都是作用在整个数组上的。因此，JAX-FLUIDS 使用 indexing/slicing 的方法来替代传统 Fortran 和 C/C++ 语言中的 for 循环。传统 CFD 求解中的很多写法都需要根据 JAX 数组的编程范式来调整。

我们给出一个关于二阶中心单元面重建过程的代码实现，如下。其中，类 CentralSecondOrderReconstruction 继承自 SpatialReconstruction。父类中包含虚方法 reconstruct_xi，子类负责实现它。该方法接受全量数组 buffer 和 重建方向 axis 作为输入参数。

from functools import partial
import jax, jax.numpy as jnp
from jaxfluids.stencils.spatial_reconstruction import SpatialReconstruction

class CentralSecondOrderReconstruction(SpatialReconstruction):

   def __init__(self, nh: int, inactive_axis: jnp.array) -> None:
      super(CentralSecondOrderReconstruction, self).__init__(
         nh=nh, inactive_axis=inactive_axis
      )
      self.slices = [
         [jnp.s_[..., self.nh-1:-self.nh , self.nhy, self.nhz], # X-DIRECTION
            jnp.s_[..., self.nh :-self.nh+1, self.nhy, self.nhz], ],
         [jnp.s_[..., self.nhx, self.nh-1:-self.nh , self.nhz], # Y-DIRECTION
            jnp.s_[..., self.nhx, self.nh :-self.nh+1, self.nhz], ],
         [jnp.s_[..., self.nhx, self.nhy, self.nh-1:-self.nh], # Z-DIRECTION
            jnp.s_[..., self.nhx, self.nhy, self.nh :-self.nh+1], ],
      ]

   @partial(jax.jit, static_argnums=(0, 2))
   def reconstruct_xi(self, buffer: jnp.array, axis: int) -> jnp.array:
      s_ = self.slices[axis]
      cell_face_state_xi = 0.5 * (buffer[s_[0]] + buffer[s_[1]] )
      return cell_face_state_xi

Buffer 数组可以根据重建方向或者问题维度的不同，进行不同的 indexed/sliced 操作。三维时，buffer 数组的 shape 为 $(5,N_x+2N_h,N_y+2N_h,N_z+2N_h)$；如果退化到二维，shape 变为 $(5,N_x+2N_h,N_y+2N_h,1)$；如果退化到一维，shape 进一步变为 $(5,N_x+2N_h,1,1)$。不同维度下，slice 操作的范围也需要相应地调整。CentralSecondOrderReconstruction 中的数据成员 self.slices 保存了各个空间方向对应数据的索引。

考虑在 $x$ 方向上进行二阶中心面重建的实践，

$${\mathbf{U}}_{i+\frac{1}{2},j,k}=\frac{1}{2}\left({\mathbf{U}}_{i,j,k}+{\mathbf{U}}_{i+1,j,k}\right)$$

我们需要两个 slice 对象：

• jnp.s_[…, self.nh-1:-self.nh, self.nhy, self,nhz] 对应 ${\mathbf{U}}_{i,j,k}$
• jnp.s_[…, self.nh:-self.nh+1, self.nhy, self,nhz] 对应 ${\mathbf{U}}_{i+1,j,k}$

其中，

• 成员变量 self.nh 表示 halo cells 的数量；
• self.nh-1:-self.nh 和 self.nh:-self.nh+1 表示重建过程要求对应的切片部分；
• self.nhy 和 self.nhz 表示另外两个方向上无需重建的切片 (如果特定方向是进行重建计算的，可以将其设置为 self.nh:-self.nh，否则设置为 None:None)；
• self.nhx，self.nhy，self.nhz 都在父类中定义。

OOP in JAX

JAX 本身是个函数式编程的框架。但是，我们在 JAX-FLUIDS 的求解器中，使用了面向对象的编程范式 (OOP)。在 JAX-FLUIDS 的开发中选择 OOP 有以下好处：

• 一个完备的 CFD 求解器通常需要提供很多的可替换的数值算法。OOP 可以将同功能的不同算法实现为不同的子类，父类中实现算法的通用部分。
• OOP 运行用户扩展新的子类，实现针对自己问题的自定义求解器。
• 再次强调，基于 JAX-FLUIDS 中优良的模块化设计，用户可以方便的集成自定义的模块和算法实现。

JIT & Pure Functions

JAX 提供了针对函数的即时编译 (JIT) 功能，可以大幅提升执行性能。但是，在使用 JIT 时，需要考虑两点限制：

• 即时编译的函数只能是纯函数 (Pure Functions)
  当一个函数在确定的输入下有确定不变的输出，并且没有副作用 (side effects)，就可以被看做是纯函数了。
• 函数内的控制流不能依赖输入参数的值
  通过 JIT 编译，函数会被编译成抽象格式，然后被缓存起来。该抽象版本的函数可以用于不同的输入值。当输入参数的类型和 shape 不发生改变的时候，函数不会被重新编译，所以函数无法感知依赖输入参数值的控制流变化。如果想要让函数控制流依赖于输入参数的值，必须将该参数声明为 static argument。如此，函数每次都会在输入参数值发生变化时重新编译。

JAX 的 JIT 编译特性对 JAX-FLUIDS 代码实现产生了一些影响：

1. 成员方法中的 self 参数必须声明为 static argument。
   这代表着类成员变量一般是不允许发生改变的 (这有点类似于 c++ 语言中的 constexpr)。

2. 由于 JIT 编译函数中的控制流只能依赖于 static argument，我们分别罗列 JAX-FLUIDS 中三种不同控制流的情况，并讨论：

   • for/while 循环的条件退出。对于最外层的主循环，不把它包含在 JIT 编译的函数中，如此无需额外的考虑。我们仅对循环中的三个计算密集型的函数 compute_timestep()，do_integration_step() 和 compute_forcings() 进行 JIT 编译。
   • 对于数据数组进行条件切片。在 JAX-FLUIDS 的代码中，经常会遇由于方向不同而对数组取不同切片大小的情况。空间方向通过输入参数 axis 表示，执行的代码控制流依赖于 axis 的值，所以 axis 必须声明为 static argument。使用 axis 作为输入参数的函数会根据 axis 的值编译多次，每个编译的版本都会被缓存。
   • 代码块的条件执行。我们前面介绍了类成员变量通常是 static 的，所以对于不同代码块的条件执行，我们通常会依赖类成员变量。这非常类似 C++ 中的 if constexpr，能在编译阶段就确定执行的代码块。

3. Element-wise 操作通常需要使用掩码 (mask)。对于 JIT 编译的函数，要求输入的数组 shape 保持不变。

下面给出了一个掩码典型应用示例 (注意，我们通常会配合 jnp.where 一起使用)：

from functools import partial
import jax, jax.numpy as jnp

class LevelsetHandler():
   def __init__(self, ...) -> None:
      pass

   @partial(jax.jit, static_argnums=(0, 3))
   def compute_levelset_advection_rhs_xi(
      self, levelset: jnp.array,
      interface_velocity: jnp.array,
      axis: int
   ) -> jnp.array:

      # LEFT AND RIGHT SIDED DERIVATIVE
      derivative_L = self.spatial_derivative.derivative_xi(
         levelset, self.cell_sizes[axis], axis, 0
      )
      derivative_R = self.spatial_derivative.derivative_xi(
         levelset, self.cell_sizes[axis], axis, 1
      )

      # UPWINDING DEPENDING ON LOCAL INTERFACE VELOCITY
      velocity = interface_velocity[axis]
      mask_L = jnp.where(velocity>= 0.0, 1.0, 0.0)
      mask_R = 1.0 - mask_L

      # RIGHT-HAND-SIDE EVALUATION
      rhs_contribution = - velocity * (mask_L * derivative_L + mask_R * derivative_R)

      return rhs_contribution

程序主循环和核心类

我们致力于将 JAX-FLUIDS 打造成一个在 ML-CFD 研究领域中便于使用的 Python 库。

如下，我们给出了跑一个流体模拟的所需的代码示例：

import json
from jaxfluids import InputReader, Initializer, SimulationManager

numerical_setup_dict = json.load(open("numerical_setup.json"))
case_setup_dict = json.load(open("case_setup.json"))

input_reader = InputReader(case_setup_dict, numerical_setup_dict)
initializer = Initializer(input_reader)
simulation_manager = SimulationManager(input_reader)

initial_buffer = initializer.initialization()
simulation_manager.simulate(initial_buffer)

用户必须提供 数值设置文件 和 用例设置文件 (json 格式，可以参考原文附录 A.22 和 A.33 中给出的 Sod 冲击管测试的设置文件)。其中，

• 数值设置文件中，可以指定模拟所需的多种不同的数值计算方法。
• 用例设置文件中需要给出模拟的各种物理值，包括空间范围和网格划分、初始和边界条件和流体属性。

基于输入文件，首先，创建一个 class InputReader 示例对象 input_reader。其中，input_reader 会对输入数据进行必要的转换和检查，确保两个文件内容是一致的。

接着，基于 input_reader 构建 class Initializer 和 class SimulationManager 对象。其中，class Initalizer 对象可以基于用例设置文件或者重启文件 (restart file) 生成初始的数据数组。调用 initializer 的 initialization 方法可以获取到初始数据数组。class SimulationManager 是 JAX-FLUIDS 的主核心类，内部实现封装了多种算法，根据数值计算文件的设置对流体进行模拟。

初始数据数组需要传入 simulation_manager 的 simulate 方法，该函数是整个模拟的入口函数。

simulate 方法包含三个主要的循环：

• 基于物理时间步的循环，参考 算法 1
• 基于 Runge-Kutta 阶段的循环，参考 算法 2
• 基于空间维度的循环，参考 算法 3

算法 1 simulate() 函数中实现的基于物理时间步的循环，被标记的函数仅在模拟流体受到主动力情况时才会被调用。

while time < end_time do
   compute_timestep()
   forcings_handler.compute_forcings()
   do_integration_step()
   output_writer.write_output()
end

算法 2 do_integration_step() 函数中实现的基于 Runge-Kutta 阶段的循环，被标记函数仅在模拟两相流时才会被调用。

while RK_stages do
   space_solver.compute_rhs()
   levelset_handler.transform_volume_averages_to_conservatives()
      time_integrator.prepare_buffers_for_integration()
      time_integrator.integrate_conservatives()
      time_integrator.integrate_levelset()
      levelset_handler.reinitialize_levelset()
      boundary_condition.fill_boundaries_levelset()
      levelset_handler.compute_geometrical_quantities()
      levelset_handler.mix_conservatives()
      levelset_handler.transform_conservatives_to_volume_averages()
      get_primitives_from_conservatives()
      levelset_handler.extend_primitives_into_ghost_cells()
      boundary_condition.fill_material_boundaries()
end

算法 3 compute_rhs() 函数中实现的基于空间维度的循环，被标记函数仅在模拟两相流时才会被调用。

while active_axis do
   flux_computer.compute_inviscid_flux_xi()
      flux_computer.compute_viscous_flux_xi()
      flux_computer.compute_heat_flux_xi()
      levelset_handler.weight_cell_face_flux_xi()
      levelset_handler.compute_interface_flux_xi()
      levelset_handler.compute_levelset_advection_rhs()
end

JAX-FLUIDS 中的梯度计算

JAX-FLUIDS 提供了 simulate 方法用于标准的正向 CFD 模拟。JAX-FLUIDS 可以和普通 CFD 求解器一样用于数据生成，开发数值算法，研究流体动力学。由于 simulate 方法没有返回值，因此，该方法不能用于端到端的优化。

为了能够在 JAX-FLUIDS 中使用自动微分，我们提供了 feed_forward 方法。该方法的输入是一个 batch 的初始数据，然后模拟固定的时间步数。用户提供积分步数和固定的时间步长，feed_forward 方法会输出一个结果轨迹。

具体而言，假设，

• 输入数据的 shape 为 $(N_b,5,N_x,N_y,N_z)$，其中 $N_b$ 是 batch size
• 输出轨迹的 shape 为 $(N_b,N_T+1,5,N_x,N_y,N_z)$，其中 $N_T$ 是积分步数

在 feed_forward 内部，通过 jax.vmap 方法实现 batch 维度的计算。feed_forward 可以被 JIT 编译，而且可以通过 jax.grad 和 jax.value_and_grad 方法进行求导。所以 feed_forward 方法可以被用于 ML 模型的端到端的优化。

JAX-FLUIDS 中 ML 模型的集成

为了集成 ML 模型，JAX-FLUIDS 需要搭配 Haiku 和 Optax 一起使用。

Haiku 是为 JAX 开发的神经网络库。在 Haiku 中，神经网络都通过 haiku.Module 类型表示。为了同 JAX 结合使用，网络的前向方法必须嵌入到一个被转换为 haiku.Transformed 类型的 wrapper 函数中。该前向 wrapper 函数提供两个函数，分别为 init 和 apply。其中，init 方法用于初始化神经网络的参数，apply 方法执行网络的前向。当执行 apply 方法时，必须显式传入网络参数。更多信息请参考 Haiku 官网文档。

Optax 提供各种优化器算法，比如 Adam 优化器。

在 JAX-FLUIDS 中，我们提供嵌入现有 ML 模型和优化 ML 模型的接口。神经网络可以被传递给 simulate 和 feed_forward 方法。

需要注意的是，仅有 feed_forward 方法是可微的，可以用于优化模型。在 ML-CFD 研究中，一个典型的方式就是使用数据驱动的 ML 模型替换掉一个传统的数值计算步骤。

JAX-FLUIDS 求解器为一些模块设计了接口以利用神经网络，比如单元面重建 (cell face reconstruction)，黎曼求解器 (Riemann solver) 或者力模块 (forcing module)。用户通过全局配置两个字典来使用神经网络 (其中，一个字典决定神经网络作用于 JAX-FLUIDS 的哪个子程序，另一个字典对应神经网络参数)。

# 验证 JAX-FLUIDS 作为经典 CFD 求解器 #

译者注：
大家知道，HPC 优先得保证精度，精度是 HPC 软件具备可用性的基本前提。本节论证 JAX-FLUIDS 求解经典 CFD 问题，求解方法与传统 CFD 求解器求解方法基本无异，但代码框架基于 JAX 框架全部重写 (传统 CFD 求解器一般采用 C/C++/Fortran 编写)，底层函数（算子库）和运行的硬件平台也都发生变化。
论文花了较多篇幅验证 JAX FLUIDS 计算结果和传统 CFD 软件保持一致，旨在说明新软件具备可用性基础。

本节验证了 JAX-FLUIDS 求解经典流体力学算例的表现，分别对 单相流 和 液固/液液两相流 进行了验证。

在本节的数值验证中，我们预设了两种数值设置：

• HLLC，采用高阶 Godunov 公式
  • 原始变量采用 WENO-JS 重构
  • 近似 HLLC 黎曼求解器
• ROE，采用通量分裂公式
  • 原始变量采用 WENO-JS 重构
  • ROE 近似黎曼求解器

具体地，耗散通量 (耗散项) 采用四阶中心差分，采用理想气体状态方程。对于单相流，CFL 数设置为 0.9，时间离散格式为 TVD-RK3；对于两相流，水平集对流方程的离散采用 HOUC5，拓展方程的空间离散采用一阶迎风格式，时间采用 Euler 差分格式，CFL 数设置为 0.7，重初始化方程采用 WENO3-HJ 结合 TVD-RK2 格式求解。

单相流

对 JAX-FLUIDS 单相流的验证包含以下几个算例：

收敛性验证

下图中，由上至下的黑线分别表示收敛速率为 $O(\Delta x^1),O(\Delta x^3),O(\Delta x^5)$，可以得出，JAX-FLUIDS 的收敛性达到预期。

Sod & Lax 激波管问题

一维激波管 (Lax shock tube) 问题 是验证可压缩 CFD 求解器的标准范例，本文以此验证数值方法在求解黎曼问题中的数值稳定性。


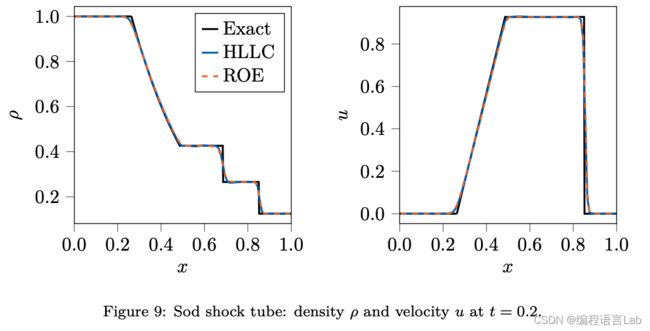
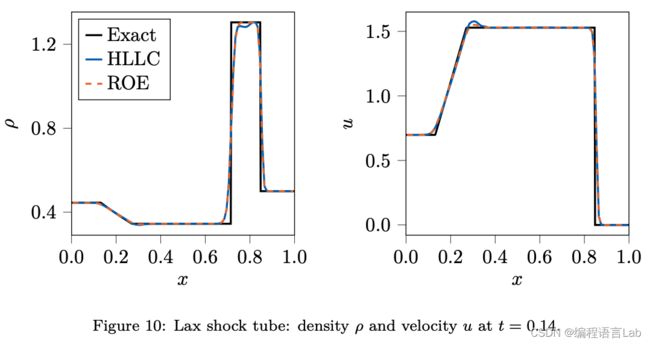
上图中，黑线表示激波管问题的精确黎曼解，两种预设数值方法 HLLC 和 ROE 都和精确解符合得很好，数值色散和耗散都处于较低的水平 (其中，HLLC 在 Lax 激波管中数值色散略高于 ROE)。

顶盖驱动流

顶盖驱动流 是流动结构简单、最经典的剪切流，常作为 CFD 数值方法的验证算例。

在 HLLC 的设置下，计算结果和公认文献中的参考结果非常符合。

可压缩的衰减各向同性湍流

前几个例子都是简单的一维/二维算例。本小节中，我们验证了 高雷诺数下的各向同性湍流。

为了平衡计算量的需求，引入了大涡模拟 (LES) 模型 ALDM，并采用 HLLC 方法作为对照，网格数分别设置为 $32^3$ 和 $128^3$。

可以看到，相比于参考 DNS 结果，$128^3$ 网格数下的 HLLC (DNS) 依然不能解析湍流的所有尺度；但相比于粗糙网格 $32^3$ 下的 DNS，LES 结果更接近于参考结果。

两相流

对于两相流，我们验证了以下算例。

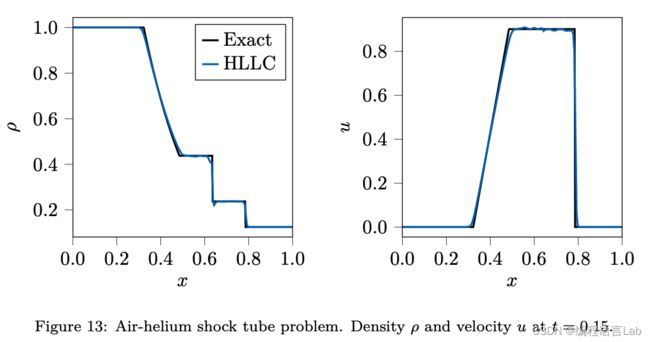
两相 Sod 激波管问题

两相激波管问题是一维激波管问题的变种，将初始条件设置为左侧为空气 (${\gamma }_{air}=1.4$)、右侧为氦气 (${\gamma }_{helium}=1.667$)，求解此时的无粘 Euler 方程。

JAX-FLUIDS 的求解结果与精确解吻合，交界面的位置以及激波速度和强度的求解都非常准确。

钝体绕流的弓形激波

弓形激波发生在超音速钝体绕流问题中，这里模拟了超音速 ($Ma=3,20$) 圆柱绕流问题，以此验证 JAX-FLUIDS 在五年无粘流体 (Euler 方程) 的流固交界面问题。

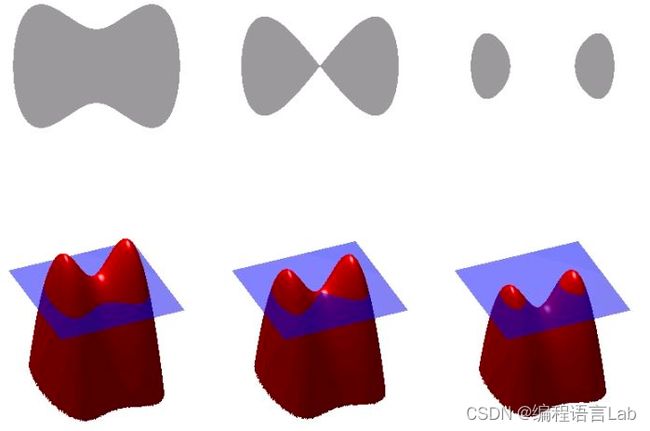
液滴的振荡变形

考虑由于表面张力和惯性的相互作用而震荡的液滴，其震荡的物理过程如下：

1. 初始状态：(横向) 椭圆形
2. 由于表面张力 —> 圆形，此过程将势能转变成动能
3. 动能 —> (纵向) 椭圆形

物理流程为：1 -> 2 -> 3 -> 2 -> 1 -> … ，如下图所示。

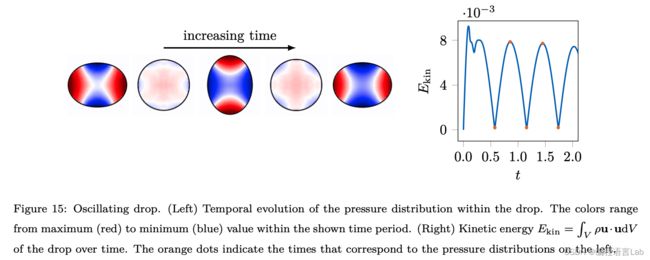
数值模拟所得的震荡周期 $T=1.16336$ 与参考理论解 $T_{ref}=1,16943$ 非常接近。

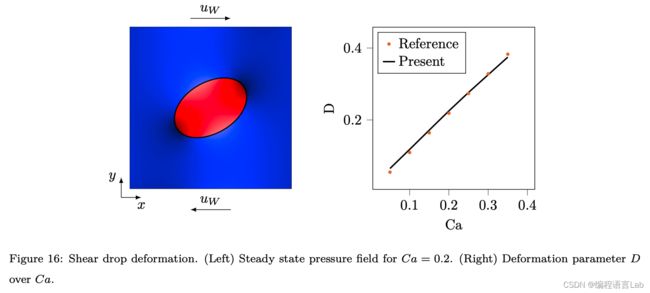
液滴的剪切变形

剪切液滴变形 可验证粘性流体 (Navier-Stokes 方程) 的液液两相交界面问题，该问题的物理过程如下：

1. 初始条件：圆形液滴，均匀剪切 (上下壁面固定速度运动)
2. 剪切 & 粘性力 —> 液滴变形 (椭圆形)
3. 最终粘性力和表面张力平衡 —> 稳态

稳态时的状态，由粘度比 ${\mu }_b/{\mu }_d$ 和无量纲数 $Ca=\frac{{\mu }_{b}Rs}{\sigma }$ 决定。其中，$R$ 表示初始液滴的半径，$\sigma$ 表示表面张力系数，$s$ 表示剪切速率，${\mu }_b$ 和 ${\mu }_d$ 分别表示介质流体和液滴的粘度。

对于小形变时，符合以下表达式，

$$D=\frac{B_1-B_2}{B_1+B_2}=Ca\frac{19{\mu }_b/{\mu }_d+16}{16{\mu }_b/{\mu }_d+16}$$

其中，$B_1$ 和 $B_2$ 分别表示稳定状态下椭圆的长半轴和短半轴。

数值模拟结果如下图所示，其结果和参考理论解吻合较好。

激波-气泡相互作用

这是一个复杂的两相测试用例，用于评估可压缩两相流数值方法的鲁棒性和有效性。该数值案例研究浸没在空气中的氦气泡被 $Ma=1.22$ 的激波击破溃灭的过程。

下图中的结果与传统 CFD 求解器结果以及实验结果吻合。

# 在单节点中的表现 #

在上一节，我们验证了 JAX-FLUIDS 作为传统 CFD 求解器的准确性。本节将验证其作为 CFD 求解器的计算效率。

• Nvidia RTX A6000 48GB
• JAX 版本：0.2.26
• 测试用例：$Ma=0.1$ 的三维可压缩泰勒-格林涡 (TGV)

测试结果如下表所示。

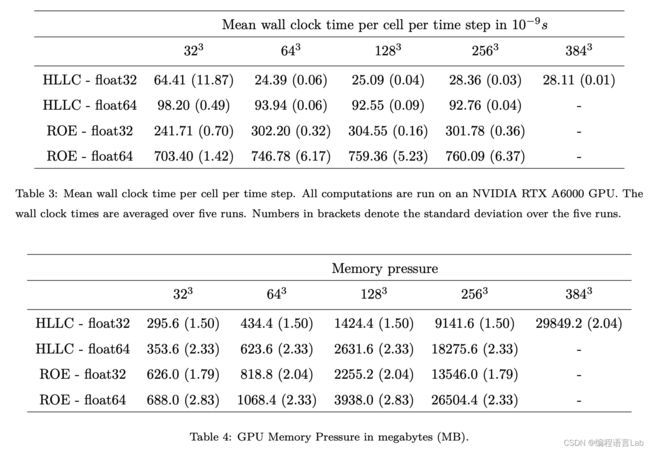
译者注：本节仅展示了 JAX-FLUIDS 的计算用时和内存占用量，没有展示传统 CFD 求解器的结果作为对比，不能得出基于高级程序语言 Python/JAX 是否有提升 or 牺牲计算效率。若是能对比 C/C++/Fortran 的 CPU 代码，以及直接基于 Cuda 的 GPU 代码，这两者的计算效率和内存占用，能给出更有意义的指导价值。(但是，这个工程量可能太大，论文不可能完全展示)。

# JAX-FLUIDS 中的机器学习 #

以上，我们展示了 JAX-FLUIDS 作为传统 CFD 求解器的方方面面，其使用与编写基本传统 CFD 求解器无异。本节将展示基于 JAX 编写的 CFD 求解器所带来的优势 (即，在能提供自动微分功能下，耦合机器学习方面的优势)。

深度学习基础

译者注：作者本节介绍了一般的监督学习范式，以 MSE 为例介绍了 MLP 及深度神经网络。

通过 PDE 的轨迹进行优化

对于监督学习，需要标签化的输入输出成对数据。而在流体力学中，复杂流动的精确解非常稀少，因此，通常会 采用高解析的数值解代替精确解。

可微分物理研究领域中的端到端的优化工作，通常采用 接收来自可微分物理求解器反向传播的梯度 来构建监督学习的 ML 模型。

这里将 ML 模型内嵌在可微分 PDE 求解器中，将 PDE 求解器正向计算得到的轨迹 (如一系列时间序列解) 和参考真轨迹进行比较，误差的导数将在时间序列上传播。

我们将轨迹的状态写作，

$$\tau =\{{\mathbf{U}}^1,\cdots ,{\mathbf{U}}^{N_T}\}$$

可微分求解器 JAX-FLUIDS 也可以被认为是一个参数化的生成器 ${\mathcal{G}}_{\theta }$，能够从初始条件 ${\mathbf{U}}_0$ 生成一个轨迹，

$${\tau }_{\theta }^{PDE}=\{{\mathbf{U}}^1,\cdots ,{\mathbf{U}}^{N_T}\}={\mathcal{G}}_{\theta }({\mathbf{U}}_0)$$

目标函数则是 ${\tau }_{\theta }^{PDE}$ 和真实轨迹 $\hat{\tau }=\{{\hat{\mathbf{U}}}^1,\cdots ,{\hat{\mathbf{U}}}^{N_T}\}$ 之间的区别。以 MSE 为例，

$${\mathcal{L}}^T=\frac{1}{N_T}\sum _{i=1}^{N_T}MSE({\mathbf{U}}^i,\widehat{{\mathbf{U}}^i})$$

误差函数关于神经网络可调参数的导数为 $\partial \mathcal{L}/\partial \theta$，该导数在模拟的轨迹中和整个可微分 PDE 求解器中反向传播，且在基于梯度的优化路线中也适用该导数来优化 ML 模型。

JAX-FLUIDS 中，ML-CFD 的多个步骤可以联合在一起。因此，ML 模型能看到求解 PDE 的全部过程，并且了解其如何影响到模拟轨迹的。这样一来，可以使得训练的模型自然地是基于特定方程和物理信息的 (这是因为，模型在训练阶段就能看到自己的输出，从而缓解了训练和测试数据集之间的分布不匹配问题)。此外，ML 模型还会考虑求解器其他部分的近似误差。

JAX-FLUIDS 允许我们通过 JAX 获取整个 CFD 模拟轨迹中任意标量观察力状态轨迹的梯度。我们强调 JAX-FLUIDS 通过复杂的子函数 (如空间重构、黎曼求解器或两相流的相互作用) 对每个时间步进行微分。

自动微分梯度的验证

本节采用一个简单的例子，验证 JAX 的自动微分梯度 和 基于有限差分得到的梯度之间的差别。

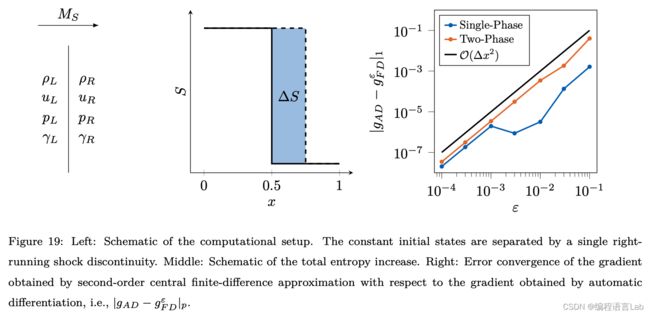
以简化的激波管问题为例，一个马赫数为 $M_s$ 的单激波传播到静止流体中，计算积分熵的增量对马赫数的导数。即，

$$g=\frac{\partial \Delta S^n}{\partial M_s}$$

从这样的一个简化的问题中，可以得出结论 对于固定的时间下，积分熵的增量只与马赫数相关。 即，

$$\Delta S^n=\Delta S(t=t^n)=\Delta S(M_S)$$

同时，采用二阶中心差分计算导数，

$$g_{FD}^{ϵ}=\frac{\Delta S(M_S+ϵ)-\Delta S^n(M_S-ϵ)}{2ϵ}$$

如下右图，我们可以得出结论，有限差分近似以二阶收敛到相应的自动微分梯度。即，通过 JAX-FLUIDS 进行自动微分是可行的，能给出正确的梯度。

一个黎曼求解器的端到端优化

本节将展示 JAX- FLUIDS 如何通过最小化预测轨迹和真实轨迹之间的损失来学习数值通量函数 (一个近似黎曼求解器)。

具体思路是，优化 Rusanov 通量函数 (也称为 Lax-Friedrichs 通量函数 ⁶)。

界面 $x_{i+1/2}$ 处的 Rusanov 通量函数构造如下，

$${\mathbf{F}}_{i+1/2}^{Rusanov}=\frac{1}{2}({\mathbf{F}}_L+{\mathbf{F}}_R)-\frac{1}{2}\alpha ({\mathbf{U}}_R-{\mathbf{U}}_L)$$

其中，${\mathbf{U}}_{L/R}$ 和 ${\mathbf{F}}_{L/R}$ 是守恒变量和通量的左侧和右侧界面重构，$\alpha$ 是标量数值粘度。

经典 Rusanov 方法的数值粘度是定义在每一个界面上的，即，

$${\alpha }_{Rusanov}=\max \{|u_L-c_L|,|u_L+c_L|,|u_R-c_R|,|u_R+c_R|\}$$

其中，$u$ 是界面的法向速度，$c$ 是当地声速。

虽然经典 Rusanov 方法能得到稳定的结果，但由于过大的数值耗散作用，使得结果模糊了 (抹平了锐化的部分)。

我们提出采用 Rusanov-NN 通量 来优化这个问题，即采用 (神经网络的输出) 新的数值耗散系数，

$${\alpha }_{Rusanov}^{NN}=NN(|\Delta u|,u_M,c_M,|\Delta s|)$$

来代替传统的数值耗散系数。其中，

$$\begin{gathered} \Delta u=|u_R-u_L| \\ {u}_M=\frac{1}{2}(u_L+u_R) \\ {c}_M=\frac{1}{2}(c_L+c_R) \\ \Delta S=|s_R-s_L| \end{gathered}$$

神经网络 NN 的结构为 三层 MLP，每层有 32 个神经元，激活函数为 ReLU()，最后一层接一个指数激活函数使得输出值大于 0，${\alpha }_{Rusanov}^{NN}>0$。

误差函数为基于 Rusanov-NN 模型求解器的预测值 (NN) 和粗糙网格 (CG, Coarse-grained) 下状态向量 ${\mathbf{W}}_i$ 的均方根误差，

$$L=\frac{1}{N_T}\sum _{i=1}^{N_T}MSE({\mathbf{W}}_i^{NN},{\mathbf{W}}_i^{CG})$$

训练数据集由前 1000 个时间步粗糙网格下的状态组成。

在训练过程中，模型以 $N_T=15$ 个时间步为一个基本训练单位；而在验证时，模型将预测完整的 2501 个时间步。

下图展示了训练结果，可以看到相比于 Rusanov 的结果，Rusanov-NN 结果更为精细，耗散效应更低。

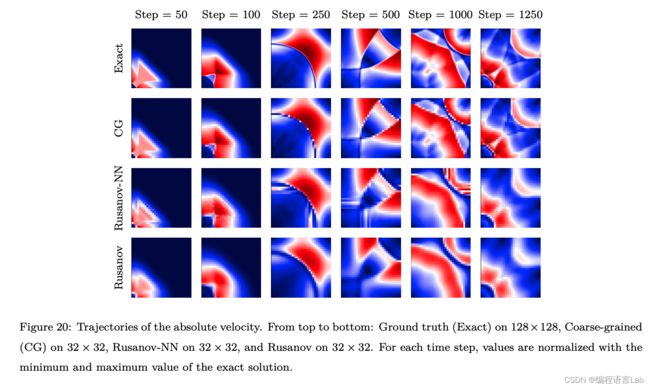
即使超过了训练集的部分 (1000 个时间步之后)，Rusanov-NN 依然比 Rusanov 的误差更低。

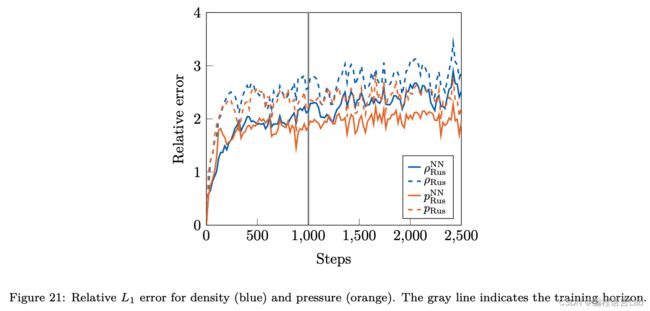
下图以本节的数值算例为例，展示了离线训练中存在的训练数据和验证数据不匹配现象，而在线训练则避免了该情况的发生。图中 $U_{t_n}^{CFD}$ 表示在时刻 $t_n$ 时由 CFD 计算得到流场的状态 (轨迹)，本例中，假设 $\alpha$ 是当地的 (local)，即能由当前时刻下的状态参数计算的到。

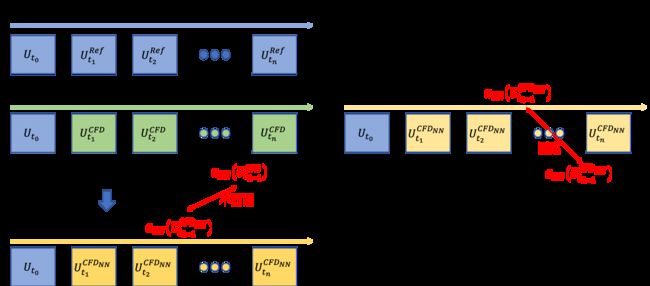
# 总结 #

本文提出了一个完全可微的可压缩三维 CFD 求解器的 Python 包 —— JAX-FLUIDS，可用于求解湍流、任意固体边界的可压缩流动和两相流。

JAX-FLUIDS 尚不能用于求解一些复杂的物理现象，如燃烧、流体结构的相互作用、空化等问题。

JAX-FLUIDS 的最大局限性还是在于可用 GPU 内存。JAX-FLUIDS 可以用于单个 GPU 下 4 亿个自由度的计算，但是在流体力学问题中往往需要更多的自由度。解决计算量过大 (GPU 显存问题) 可以通过 自适应的多分辨率方法 和 多 GPU 并行的方法。前者需要在计算中不断修改计算网格 (张量图的大小和规模)，这在静态计算图的 JAX 中似乎不适用；针对后者，JAX 在最新版本中提供了许多不同的 GPU 并行策略。

# 作者介绍 #

Nikolaus A. Adams，慕尼黑工业大学教授，担任空气动力学与流体力学研究所所长、首席教授及机械工程系主任，美国物理学会会士，德国自然科学基金会 (DFG) 重大战略项目 (SFB) 首席科学家，此外，还担任清华大学名誉客座教授，西北工业大学授予“顾问教授”等。

Adams 教授的研究兴趣广泛，在数值算法和流体物理领域都有很深的造诣，主要研究内容包括流动的物理机理、多尺度流动的建模与模拟、复杂流体及基础研究的实际应用。目前担任计算物理顶刊《Journal of Computational Physics》的执行编辑。

Adams 教授于 2000 年获得欧洲应用科学计算方法共同体 O.C. Zienkiewicz 奖，并于 2013 年获得高性能计算领域最高学术奖项 Gordon Bell 奖。

Adams 教授还是欧洲研究理事会 (ERC) 高级资助基金获得者，著有 3 本专著，并在《Journal of Computational Physics》、《Journal of Fluid Mechanics》、《Physics of Fluids》、《Physics Review E》等国际知名期刊上发表论文 200 多篇 (SCOPUS 统计)。

参考

---

1. James Bradbury, Roy Frostig, Peter Hawkins, Matthew James Johnson, Chris Leary, Dougal Maclaurin, George Necula, Adam Paszke, Jake VanderPlas, Skye Wanderman-Milne, and Qiao Zhang. JAX: composable transformations of Python+NumPy programs, 2018. ↩︎

2. Wikipedia: Navier–Stokes equations. https://en.wikipedia.org/wiki/Navier–Stokes_equations ↩︎

3. PhiFlow: A differentiable PDE solving framework for machine learning. https://github.com/tum-pbs/PhiFlow ↩︎

4. JAX-CFD: Computational Fluid Dynamics in JAX. https://github.com/google/jax-cfd ↩︎

5. JAX-MD: Differentiable, Hardware Accelerated, Molecular Dynamics. https://github.com/google/jax-md ↩︎

6. Wikipedia: Lax–Friedrichs method. https://en.wikipedia.org/wiki/Lax–Friedrichs_method ↩︎