python、lingo、matlab实现弗洛伊德（Floyd）算法--最短路径问题

引言

Floyd算法是一个经典的动态规划算法。是解决任意两点间的最短路径(称为多源最短路径问题)的一种算法，可以正确处理有向图或负权的最短路径问题。

Floyd 算法是一个基于「贪心」、「动态规划」求一个图中所有点到取余各点最短路径的算法。

目录

引言

问题描述

最短路径问题

算法思想 

操作步骤

实现过程

代码实现

python实现如下

 matlab实现如下

lingo实现如下

---

问题描述

最短路径问题

最短路径问题一直是图论研究的热点问题。例如在实际生活中的路径规划、地图导航等领域有重要的应用。关于求解图的最短路径方法也层出不穷，本篇文章将详细讲解图的最短路径算法。最短路径问题的背景问题一般是类似：已知各城市之间距离，请给出从城市A到城市B的最短行车方案 or 各城市距离一致，给出需要最少中转方案。简而言之：固定起始点的情况下，求最短路。

 

算法思想 

首先根据图将各个点与其余各点的距离写成矩阵的形式，依次将各个点作为中转点进行迭代，重新计算各个点与其余各点的最小距离，直至迭代点总数次，此时各点到其余各点的距离就是点到其余各点的最小路径。

操作步骤

为了计算方便，令网络的权矩阵为，为到的距离。

其中

（1）输入权矩阵。

（2）计算        其中

（3）中的元素就是到的最短路长。

实现过程

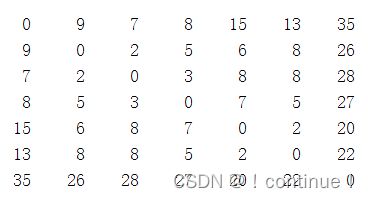
（1）根据图将各个点与其余各点的距离写成矩阵的形式。

这里的“1000”是指本身到是没有路径的应该标为无穷但是为了方便我们进行计算，这里使用1000代替无穷。

 （2）将点作为中转点进行迭代，重新计算各个点与其余各点的最小距离。

 （3）将点作为中转点进行迭代，重新计算各个点与其余各点的最小距离。

 （4）将点作为中转点进行迭代，重新计算各个点与其余各点的最小距离。

 （5）将点作为中转点进行迭代，重新计算各个点与其余各点的最小距离。 

  （6）将点作为中转点进行迭代，重新计算各个点与其余各点的最小距离。 

  （7）将点作为中转点进行迭代，重新计算各个点与其余各点的最小距离。  

 

 （7）将点作为中转点进行迭代，重新计算各个点与其余各点的最小距离。  

 我们可以比较容易从图中观察出各点到其余点的最短路径。

代码实现

python实现如下

class Graph:
    def __init__(self,num):
        self.data_li = [[1000 for i in range(num)] for i in range(num)]

    def add_edge(self, data):  # 记录各点到可到达的其余点的路径长度
        for i in data:
            self.data_li[i[0]][i[1]] = i[2]

    def floyd(self,num):
        for i in range(1,num):
            for j in range(num):
                for k in range(num):
                    if self.data_li[j][k] > self.data_li[j][i] + self.data_li[i][k]:
                        self.data_li[j][k] = self.data_li[j][i] + self.data_li[i][k]
        return self.data_li
if __name__ == '__main__':
    data = [(0,1,10),(1,0,10),(0,2,7),(0,3,8),(1,2,2),(1,4,6),(2,3,3),(2,4,9),(2,5,9),(3,5,5),(4,6,20),(5,4,2),(5,6,30),(2,0,7),(3,0,8),(2,1,2),(4,1,6),(3,2,3),(4,2,9),(5,2,9),(5,3,5),(6,4,20),(4,5,2),(6,5,30),(0,0,0),(1,1,0),(2,2,0),(3,3,0),(4,4,0),(5,5,0),(6,6,0)]
    d = Graph(7)
    d.add_edge(data)
    for i in d.floyd(7):
        print(i)

 matlab实现如下

data_li = xlsread("C:\Users\24453\Desktop\数学建模题\Dijkstra.xlsx",1,'$A$1:$G$7');
num = 7;
data = floyd(num,data_li);
function data = floyd(num,data_li)
    for i = 2:num
        for j = 1:num
            for k = 1:num
               if data_li(j,k) > data_li(j,i) + data_li(i,k)
                   data_li(j,k) = data_li(j,i) + data_li(i,k);
               end
            end    
        end
    end
    data = data_li;
end

lingo实现如下