python、lingo、matlab实现迪杰斯特拉(Dijkstra)算法--最短路径问题

引言

迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。 它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。 基本思想通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。

迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。 
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。

目录

引言

问题描述

最短路径问题

算法思想

操作步骤

实现过程

代码实现

python实现如下

matlab实现如下

lingo实现如下

---

问题描述

最短路径问题

最短路径问题一直是图论研究的热点问题。例如在实际生活中的路径规划、地图导航等领域有重要的应用。关于求解图的最短路径方法也层出不穷，本篇文章将详细讲解图的最短路径算法。最短路径问题的背景问题一般是类似：已知各城市之间距离，请给出从城市A到城市B的最短行车方案 or 各城市距离一致，给出需要最少中转方案。简而言之：固定起始点的情况下，求最短路。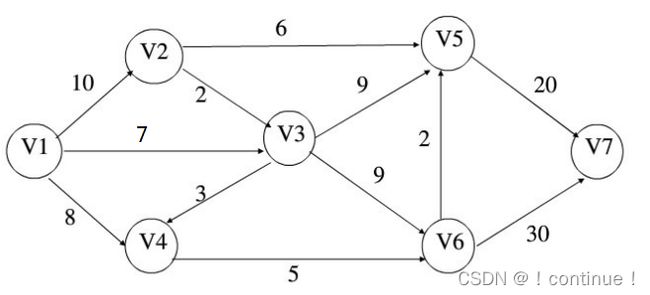

算法思想

采用标号法。可用两种标号：T标号与 P 标号，T标号为试探性标号（tentative label），P 为永久性标号（permanent label），给 点一个P表示从到点的最短路权， 点的标号不再改变。给 点一个 T 标号时，示从到点的估计最短路权的上界，是一种临时标号，凡没有得到 P 标号的点都有 T 标号。算法每一步都把某一点的 T标号改为 P 标号，当终点得到 P 标号时，全部计算结束。对于有n个顶点的图，最多经 n-1步就可以得到从始点到终点的最短路。

操作步骤

(1)给以P 标号，P()=0,其余各点均给 T标号， T()=+ ∞。

(2)若点为刚得到P 标号的点，考虑这样的点 ：(，)属于 E, 且为T标号。对 的T标号进行如下的更改：
T() = min[T（），P（） +]

(3) 比较所有具有 T标号的点，把最小者改为 P标号，即

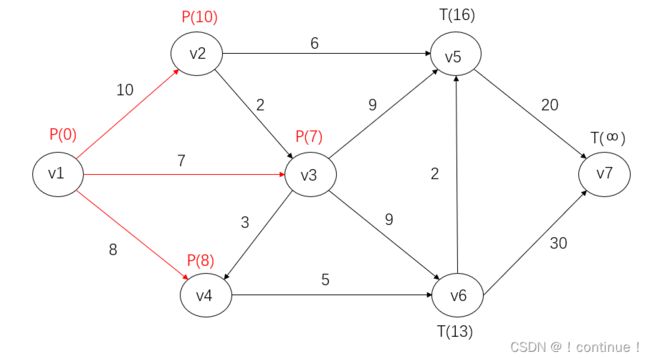
实现过程

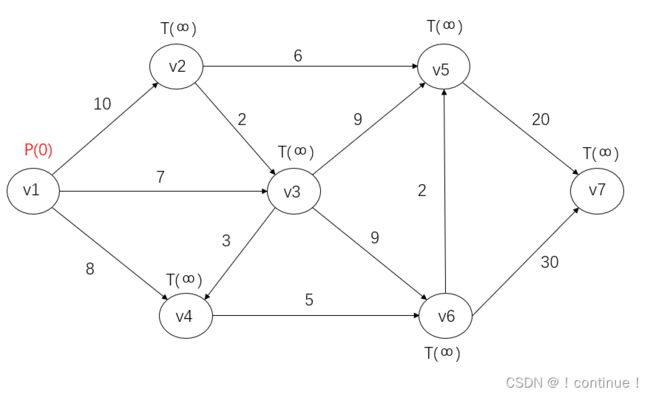
（1）首先给以P标号，＋∞，给其余所有点T标号：

 T()=+ ∞ 

（2）由于边属于E，且为T标号，所以修改这三个点的标号：

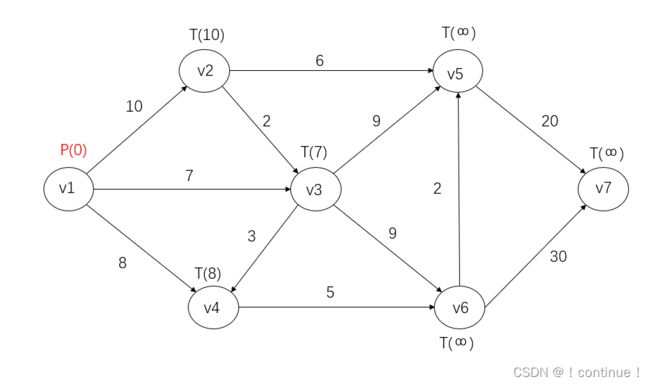
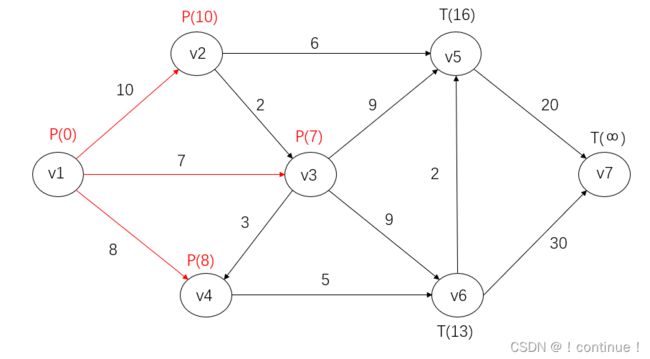
 （3）比较所有T标号，最小，所以令。并记录路径。

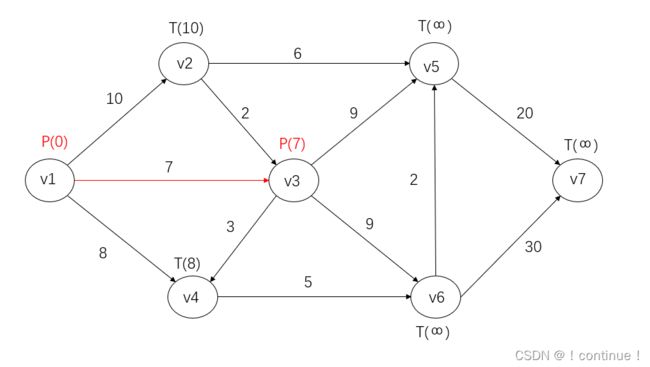
 （4）为刚得到P标号的点，考察的端点。

​​​​​​

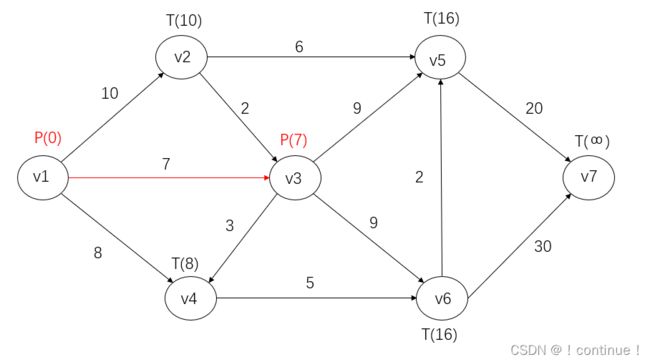
 （5）全部T标号，最小，所以令。并记录路径。

（6） 为刚得到P标号的点，考察的端点。

 （7）全部T标号，最小，所以令。并记录路径。

 

  （8）为刚得到P标号的点，考察的端点。

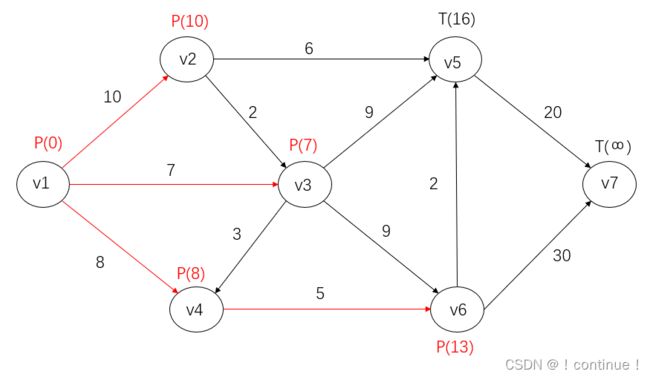
（9）全部T标号，最小，所以令。并记录路径。

  （10） 为刚得到P标号的点，考察的端点。

  （11）全部T标号，最小，所以令。并记录路径。

 （12） 为刚得到P标号的点，考察的端点。

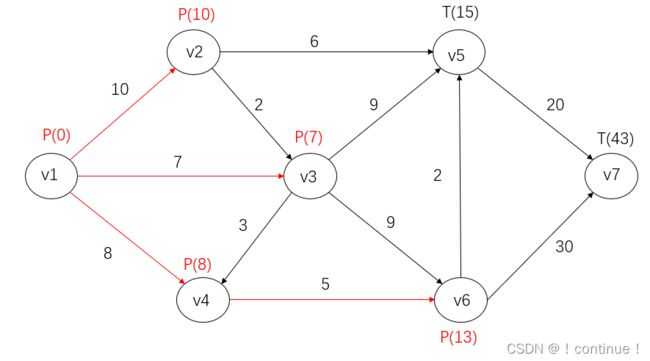
 （13）全部T标号，最小，所以令。并记录路径。

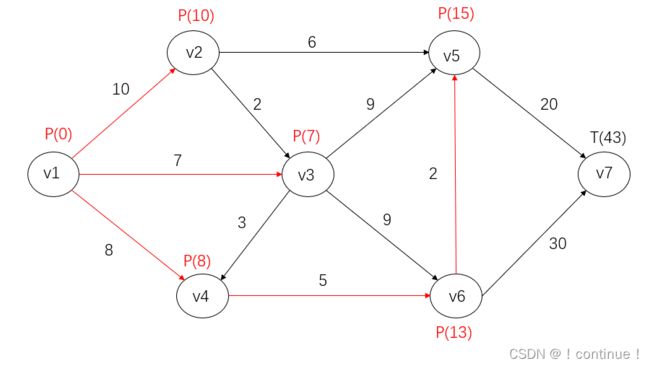
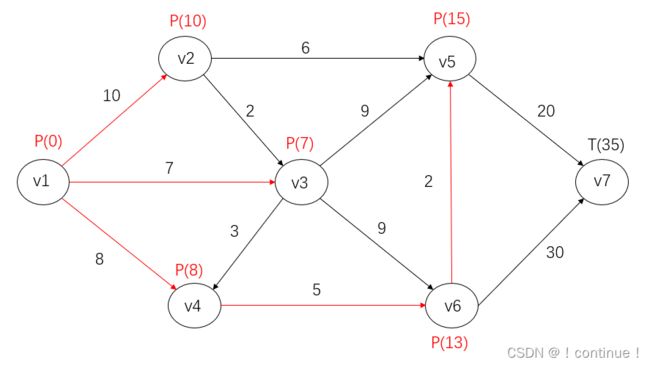
 自此全部点都已标完P标号，由此可知到的最短路径为：，路长为，同时得到到其余各个点的最短路。

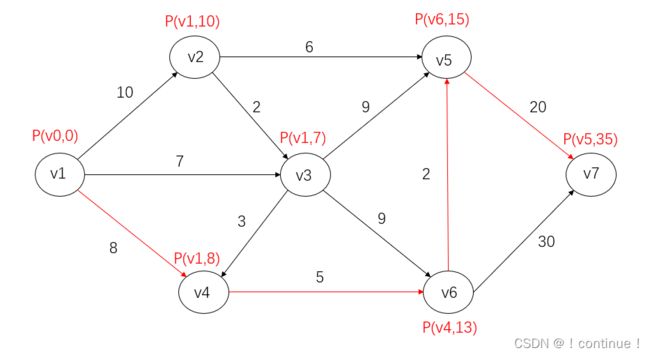
 如果你不能从图像中直接看出最短路，可以标记P如这种形式：

这样就可以比较容易从终点开始逆推找到最短路径。

代码实现

python实现如下

class Graph:
    def __init__(self,num):
        self.data_li = [['inf' for i in range(num)] for j in range(num)]    #创建一个记录每个点到其余个点的路径长度的表，开始时全为inf
        self.path = ['inf' for i in range(num)]
        self.mark = []              #用于记录已经标记过的点
        self.distance = ['inf' for i in range(num)]          #记录目前起始点到其余个的最短距离

    def add_edge(self,data):  #记录各点到可到达的其余点的路径长度
        for i in data:
            self.data_li[i[0]][i[1]] = i[2]

    def dijkstra(self,start):
        self.mark.append(start)
        self.distance[start] = 0
        que = []
        que.append(start)
        while que:
            curnode = que.pop(0)
            for i in range(len(self.data_li[curnode])):
                if i not in self.mark:
                    if  self.distance[i] == 'inf':
                        if self.data_li[curnode][i] == 'inf':
                            continue
                        else:
                            self.distance[i] = self.distance[curnode] + self.data_li[curnode][i]
                            self.path[i] = curnode
                            continue
                    if self.data_li[curnode][i] == 'inf':
                        continue
                    else:
                        if self.distance[curnode] + self.data_li[curnode][i] < self.distance[i]:
                            self.distance[i] = self.distance[curnode] + self.data_li[curnode][i]
                            self.path[i] = curnode
            cur_min_val = [self.distance[i] for i in range(len(self.distance)) if i not in self.mark and self.distance[i] != 'inf']
            if cur_min_val:
                cur_min_val = min(cur_min_val)
                for i in range(len(self.distance)):
                    if i not in self.mark:
                        if self.distance[i] == cur_min_val:
                            self.mark.append(i)
                            que.append(i)
        li = []
        li.append(len(self.path))
        a = len(self.path)-1
        while a:
            if self.path[a] == 'inf':
                break
            else:
                li.insert(0,self.path[a])
                a = self.path[a]
        return li
if __name__ == '__main__':
    data = [(0,1,8),(0,2,10),(0,3,15),(1,4,9),(1,5,11),(2,5,8),(2,6,6),(3,6,14),(4,7,8),(5,7,9),(6,7,10)]
    d = Graph(8)
    d.add_edge(data)
    print(d.dijkstra(0))

matlab实现如下

mark = [];                          %用于记录已经标记过的点
distance = ones(1,7);               %记录目前起始点到其余个的最短距离
distance = distance * 100;
position = ones(1:7);                      %记录新标记的点的来自哪个点
position = position * 100;
data_li = xlsread("C:\Users\24453\Desktop\数学建模题\Dijkstra.xlsx",1,'$A$1:$G$7');
start = 1;
path = dijkstra(start,data_li,mark,distance,position);
function path = dijkstra(start,data_li,mark,distance,position)
    mark = [start];
    position = [start];
    distance(start) = 0;
    que = [start];
    while que
       curnode = que(1);
       que = que(1,2:end);
       for i = 1:length(data_li(curnode,:))
           if ismember(i,mark) == 0
              if distance(i) == 100
                 if data_li(curnode,i) == 100 
                    continue
                 else
                     distance(i) = distance(curnode) + data_li(curnode,i);
                     position(i) = curnode
                     continue
                 end
              end
              if data_li(curnode,i) == 100
                  continue
              else
                  if distance(curnode) + data_li(curnode,i) < distance(i)
                     distance(i) = distance(curnode) + data_li(curnode,i);
                     position(i) = curnode
                  end
              end  
           end
        end
        cur_min_val = [];
        for i = 1:length(distance)
            if ismember(i,mark) == 0 & distance(i) ~= 100
                cur_min_val = [cur_min_val,distance(i)];
            end
        end
        if cur_min_val
           cur_min_val = min(cur_min_val); 
           for i = 1:length(distance)
                if ismember(i,mark) == 0
                    if distance(i) == cur_min_val
                       mark = [mark,i];
                       que = [que,i];
                    end
                end
           end
            
        end   
    end
    path = [];
    path = [path,length(position)];
    a = length(position);
    while a
       if position(a) == 1
           break
       else
           path = [position(a),path];
           a = position(a);
       end
    end
    path = [1,path];
end

lingo实现如下