【Python习题集5】函数的设计
函数的设计
- 一、实验内容
- 二、实验总结
一、实验内容
1.编写两个函数分别按单利和复利计算利息,根据本金、年利率、存款年限得到本息和和利息。调用这两个函数计算1000元在银行存3年,在年利率是6%的情况下,单利和复利分别获得的本息和和利息。单利计算指只有本金计算利息。复利计算是指不仅本金计算利息,利息也计算利息,也就是通常所说的“利滚利”。如这题按单利计算本息和1000+1000×6%×3=1180元,其中利息为180元;按复利计算本息和1000×(1+6%)3=1191.016元,其中利息为191.016元。
(1)源代码
def simple_interest(money,rate,years):
interest=money*rate/100.0*years
sum_money=money+interest
return sum_money,interest
def compound_interest(money,rate,years):
sum_money=money*(1+rate/100.0)**years
interest=sum_money-money
return sum_money,interest
money=1000
rate=6
years=3
aa=simple_interest(money,rate,years)
bb=compound_interest(money,rate,years)
print("本金:",money,"\n年利率:",str(rate)+"%","\n存款年限:",years)
print("单利:","\n本息和:","%.3f"%aa[0],"利息","%.3f"%aa[1])
print("复利:","\n本息和:","%.3f"%bb[0],"利息","%.3f"%bb[1])
2.编写函数,判断一个数是否为素数。调用该函数判断从键盘中输入的数是否为素数。素数也称质数,是指只能被1和它本身整除的数。
(1)源代码
def prime(x):
flag=True
for i in range(2,x//2+1):
if x%i==0:
flag=False
break
return flag
#主程序
x=int(input("请输入一个整数:"))
if prime(x):
print(x,"是素数")
else:
print(x,"不是素数")
3.编写函数,求出一个数除了1和自身以外的因子。从键盘输入一个数,调用该函数输出除了1和它自身以外的所有因子。
(1)源代码
def zi(n):
a=[]
for i in range(2,n//2+1):
if n%i==0:
a+=[i]
return a
x=int(input("请输入一个整数:"))
print("除1和自身以外的因子:",zi(x))
4.编写函数,判断一个数是否为水仙花数。调用该函数打印出1000以内的所有水仙花数。水仙花数是指一个n位数(n≥3),它的每个位上的数字的n次幂之和等于它本身。例如:13+53+33=153,则153是水仙花数。水仙花数只是自幂数的一种,严格来说三位数的3次幂数才成为水仙花数。
(1)源代码
def flower(x):
a=x//100
b=(x %100)//10
c=(x %100)%10
if a**3+b**3+c**3==x:
return True
else:
return False
#主程序
print("1000以内的水仙花数为:")
for i in range(100,1000):
if flower(i):
print(i)
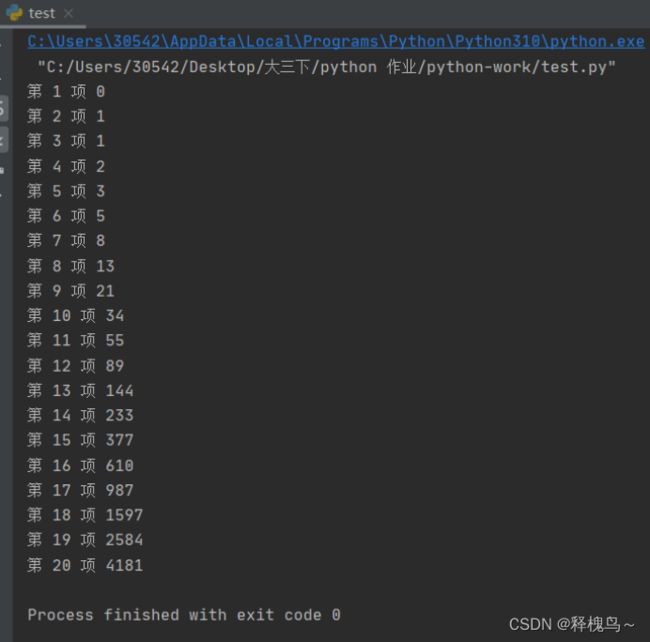
5.编写函数求斐波拉契数列的前20项。斐波拉契数列的第1项和第2项分别是0和1,从第3项开始,每一项都是前两项之和。如:0,1,1,2,3,5,8,13,21…。试用递归函数实现。
(1)源代码
def fibo(n):
if n==1:
s=0
elif n==2:
s=1
else:
s=fibo(n-1)+fibo(n-2)
return s
for i in range(1,21):
print("第",i,"项",fibo(i))
二、实验总结
- 函数是组织好的、实现单一功能或相关联功能的代码段。我们可以将函数视为一段有名字的代码,这类代码可以在需要的地方以“函数名()”的形式调用。
- 函数式编程具有以下优点:
将程序模块化,既减少了冗余代码,又让程序结构更为清晰;提高开发人员的编程效率;方便后期的维护与扩展 - 我们通常将定义函数时设置的参数称为形式参数(简称为形参),将调用函数时传入的参数称为实际参数(简称为实参)。函数的参数传递是指将实际参数传递给形式参数的过程。函数参数的传递可以分为位置参数传递、关键字参数传递、默认参数传递、参数的打包与解包以及混合传递。
- 无论实参采用位置参数的方式传递,还是关键字参数的方式传递,每个形参都是有名称的,使用符号“/”来限定部分形参只接收采用位置传递方式的实参。
- 函数在定义时可以指定形参的默认值,如此在被调用时可以选择是否给带有默认值的形参传值,若没有给带有默认值的形参传值,则直接使用该形参的默认值。
递归函数
(1)函数在定义时可以直接或间接地调用其他函数。若函数内部调用了自身,则这个函数被称为递归函数。
(2)递归函数在定义时需要满足两个基本条件:一个是递归公式,另一个是边界条件。其中: 递归公式是求解原问题或相似的子问题的结构; 边界条件是最小化的子问题,也是递归终止的条件。
(3)递归函数的执行可以分为以下两个阶段: 1.递推:递归本次的执行都基于上一次的运算结果。 2.回溯:遇到终止条件时,则沿着递推往回一级一级地把值返回来。