全面理解网络流中的最大流问题

网络流（最大流问题）

前序

在将网络里实现算法之前，我们得聊聊网络流究竟是个什么东西，毕竟只有知道它的样貌，才能继续看懂下面的定义，对吧？

---

首先，网络流不仅仅指的是什么FF算法、dinic算法。算法只是用来解决问题的（稍后我们会更加能体会这一点），而网络流，指的就是这一系列存在图论中的，关于“流（Flow）”的问题。

参考：Network flow problem - Wikipedia

网络流中有以下几种问题：

• 最大流问题
• 最小费用流问题
• 多商品流问题(multi-commodity flow problem)
• 非零流问题(Nowhere-zero flow)

本文着重于最大流问题，阐述其问题和算法的过程和个人理解，方便其他人学习。

文章目的

个人某天刷leetcode的时候遇到了网络流算法。于是为了扩展知识面我便到处找关于网络流算法的文章和视频去看，但是无论是OIer的视频还是其他CSDN的文章都不免省略了很多……呃，也不是说是细节，而是更多的关于算法本身理解的部分，尤其是在所有人都对反向边的建立解释为“反悔”一词，大家的理解如此一致使得初学者很难去好好的理解算法本身。

这就好像老师强行要求学生按照某一既定方式去理解世界一样，不是说老师的方法是错误的，而是——有些人其实思维方式很可能和老师不同，这样它就很难按照老师的思路去学习。

所以本文的目的就是——不说是发明吧，尽量用一些方法对最大流问题以及其算法本身有着更多的解释（理解），方便后来人能够全面的学习。

那么，我们就开始吧。

最大流问题

对于问题最好的理解就是问题本身。

查一下百度就能知道，一个名字叫T.E.哈里森的人在1955年提出了铁路网络中两点间最大运输量的问题。不仅如此，这货为此还发了一个60余页的论文，从此成为了折磨后人的罪魁祸首。

我找到了他的论文，看看他究竟为什么想出这个破问题的。

原文：https://ntlrepository.blob.core.windows.net/lib/13000/13200/13238/AD093458.pdf

---

ps：个人实在是没有太多的精力去研究论文本身，而且论文似乎设计了一些铁路相关的背景知识，所以我并不打算讲解。此处引用文章只是为了追溯问题本身，了解一些背景知识。

---

论文一开始哈里森就指出了这篇论文的目的(Purpose of this paper)。大致的意思就是，论文的目的并不是为了让使用计算机的新手也能代替一些能够预测铁路运输量的专家，相反，专家就应该去做专家的事情。

哈里森说，当前（1954年）的铁路专家都是依靠经验去做事，很少和数字打交道（应该指的是很多专家没有数学建模的能力）。所以他们得出的结论往往含有很多的人为因素。“在专家们做出有效的估测之前，长时间的艰苦研究和计算是必不可少的”，哈里森说。

但另一方面，在面对无数问题甚至规划战役的时候，他们往往急需计划的结果，无法等待专家们去计算其中的细节。

因此，提供一种帮助专家快速、准确的预估方法将会有很大帮助。

这就是最大流问题的来源，甚至可以说这是所有算法的来源。在实际问题中抽象出数学，然后使用数学的方法解决数学的问题。

算法的根本目的就在于此，甚至数学的目的也是这样。

我们听到了太多关于知识本身的质疑，即便是我，也曾思考过数学的用途，甚至是他的意义。

结论其实非常简单——用数学（算法）抽象，然后用数学（算法）解决，最后用数学（算法）套用。

数学（算法）成为了问题和解决方案之间的桥梁，我们深入算法，就是深入问题本身。

---

最大流求解

基本定义

• 有向网络

  首先，我们要做的就是将实际问题抽象。以上面铁轨网络为例子，如何抽象火车网络成为一种数学模型？

  噢，即便你没有学过图论，凭借直觉你也能想到。车站可以作为点，铁轨作为线，然后用线把点连起来，这样不就是表示出火车网络了吗？

  是的，你想没错。不过你还可以想的更深——火车的行驶当然有方向，尤其是在我们想要求解特定两点之间的情况下，所以作为铁轨的线应该改成向量。

  OK了，这样我们就完成了初步建模，离最终数学的答案更近了一部。

  恭喜你，建立了一个有向图

• 容量

  唔……好像还差一些东西。网络有了，流呢？不要着急，我们在建立流的概念之前还有一些东西需要确定下来。

  每列火车都有承载量，理所应当的，刚刚建立的有向图中每个向量也应当有一个容量值，限制了这条边所能运输的最大货量。

• 流

  你可能会想流是怎样的定义的？其实关于流的定义大家感受一下就好，甚至直接按照字面意义理解也不为过。电流的流、河流的流、最大流的流，都差不多。

  不过我还是贴出流在wikipedia中的定义：
  

  一个流是一个满足以下要求的映射 f : E -> R

  • 容量限制：每条边的流≤该边的容量。
  • 流守恒：流入一个节点的流总和=流出该节点的流的总和

  流量代表着从源点流入汇点的流的数量

嗯……让我想想还差什么东西……对了！

怎么能少了真正的图呢，这才是最重要的，一张图就可以代表所有的定义，很简单，也直观，对吧？

人工解决

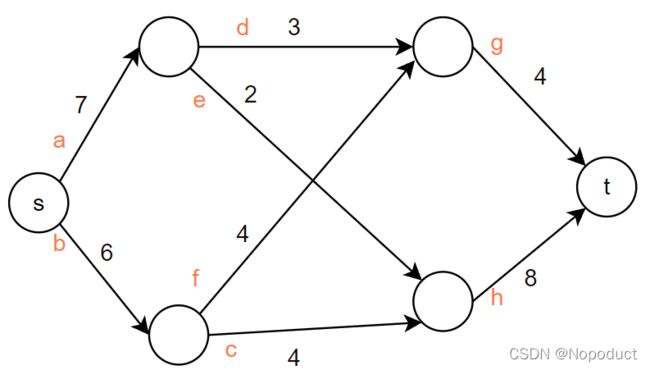
趁着图还在上面，我们人工算一下这个网络中的最大流。

我们把源点、汇点和边的代号给编辑一下。

从S汇出的流能走几条路？

• a-d
• b-c-d
• b-e-f

三条，这三条路中的流量是多少？

• a-d：8，因为a是8限制了流
• b-c-d：3，但是除了因为c限制了3的流量之外，还有另一件事需要注意。因为a-d这条路占用了d中的8个容量，所以在进行b-c-d计算的时候要记住，3的由来是min(10,3,4).
• b-e-f：3，因为min(7,3,5)

于是，总的流量加起来是8+3+3 = 14

看起来还是挺好弄得吗，似乎只要遍历每条路，然后便利的时候每条边取最小值然后减去最小值就行了。

OK，换了例子。例子取自电子科技大学的视频

我先求得该图得最大流

• a-d-g：3
• a-e-h：2
• b-f-g：1 = min(6,4,1)
• b-c-h：4 = min(5,4,6)

最大流为10。

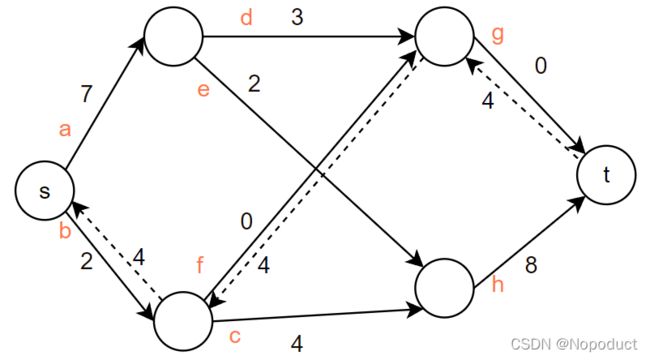
接下来我们将引出计算机得缺陷了——他不懂顺序得重要性。我们首先遍历从a边出去的流，得到的答案没什么问题，但是计算机不知道，我们完全无法得知他会先计算那条边，假设我们先从b边开始

• b-f-g：4
• b-c-h：2 = min(2,4,8)
• a-d-g：0 = min(7,3,0)
• a-e-h：2 = min(7,2,6)

最终，我们得出图的最大流为8。

这就是计算机的问题所在，我们需要招到一种方法（算法），让计算机能够不在乎先后完美的计算出正确的答案。

问题分析

我们不妨分析分析为什么顺序会影响结果。

当我们率先计算b-f-g这条边的时候，我们贪心的把整条路都填满，导致g的容量全部被来自b的量占据了。这代表着a无法再利用这条边，只能向下从e流出。

甚至我们可以想象，在复杂的网络中，一个节点的流出的边很可能全部被其他流占用，导致流向该节点的“货物”全部失效了。如果这部分货物占据了总流量的很大部分，那么结果就很有可能出现错误。

为了避免这个现象Ford-Fulkerson算法建立了反向边，即“反悔”机制。

它，是这样做的。

算法沿着路径反向建立额外的路，这条额外的路的容量就等于整条路的流量。

此时，我们完成了第一步，即b-f-g：4

然后我们继续

• b-c-h：2
• a-d-f’-c-h：2
• a-e-h：2

最大流4+2+2+2=10。结果正确。

在这里你能看到“反悔”机制是如何作用的，他将多余的流量回退。本来正确的路线是b-f-g：1，结果我们因为顺序的不同导致b-f-g率先占据更多的容量，而反向边的建立使得我们有机会将多余的3份流量回退回去，产生正确的结果。

到这里其实你已经能懂个大概了，甚至也许你不要更精进一步，对于FF算法最核心部分的反向边建立的必要性已经得知了之后你便可以直接去看算法源码，然后再着基础上去看EK算法以及Dinic算法，接下想必对于你来说只是时间问题了。

---

额外内容

真的反悔了吗？

而我接下来要反驳一下“反悔”这个理解（注意，我并非反对这个机制，而是“反悔”这个词的用法。）

请看下面的例子：

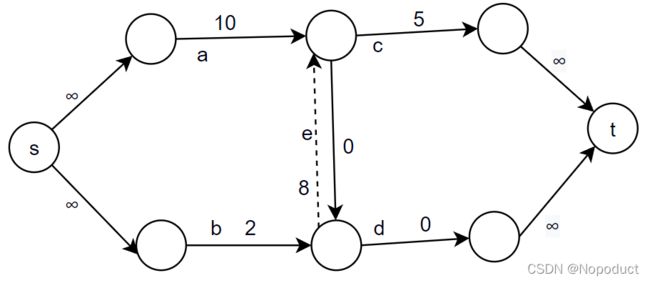
按照FF算法求最大流是12。

FF算法是一种贪心算法，它总是尽可能沾满一条边的容量。比如从a-c这条路走，它会送出去5的流量，而非3或4。这个概念其实相当重要。

正确计算顺序是这样的：

• a-c：5
• a-e-d：5
• b-d：2

但顺序打乱一下，同时建立反向边：

• a-e-d：8
• a-c：2
• b-e’-c：2

结果正确，但是这个时候我们再以“反悔”的视角来看，按照刚才的顺序，a-e-d这条路应该是5，应该反悔3个流才能得到正确的答案，但是这里我们仅仅反悔了两个流，也就是说，现在成了这个样子：

• a-e-d：8-2=6
• a-c：2+2=4
• b-d：0+2=2

a的分配明显不符合贪心的思想。

但关键就在于这一点，即便不符合贪心，即便没有完全的“反悔”，算法依旧健壮，依旧完美的运作，其中所蕴含的数学究竟是什么？是什么保证了它如此完美的运作？

接下来，才是我想讨论的重点。

---

不是“反悔”，是“借用”

接下来我们将进行一系列的分类讨论，可能会有点绕，有点晕，所以我尽量讲的清晰一点。

为了使例子更具有普遍性，我们讲每条边的容量值用任意值代替。

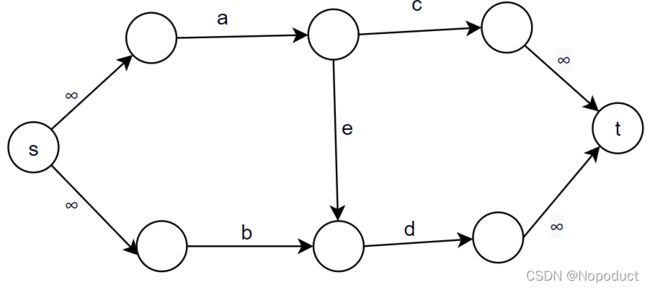
好吧，我的字母好像两条边标反了，不过不用在意，都是一样的。

1. a先走c：这个时候我们先让a优先占用c边，有两种情况。

   • a
   • a>c：当a大于c时，那么a剩余的流量会走e同时建立反向边。但是这个时候反向边也是无用的，试想，当b流通过反向边来到c时，发现c的容量早已经被a占满了。所以反向边的建立起不到任何作用，b还是老老实实走d才行。

   可以看到，a先走c是符合我们计算顺序的，这个时候无论建不建立反向边都是不影响结果的。

2. a先走e：两种情况

   • a
   • b+e
   • 如果b不走反向边，正常运作
   • 如果b走反向边，那么b就会和反向边的容量判断大小，之后剩余容量肯定能走d，通过反向边的流量则借用原来a需要走的c边。
3. b+e>d：这个时候b的剩余容量就必须要走反向边，借用a原来走的c边。
4. a>e：如果a有剩余流量，它会讲剩余流量走c边，同时建立反向边让b边有机会借用c自己的c边，防止b被阻塞。

好吧，我承认上述的分类有些乱糟糟的，确实这方面也不太好说，所以我下面以一种方便的形式展示一下 “借用” 的意思。

---

当a流来到中间上面的节点的时候，它会发现有两条路，分别是e和c。而a最讨厌选择了，因为选择意味着你需要照顾其他路的情况。

a完全不知道它流向的路是否被其他流共享，比如说当a流流向e-d的时候，它完全不知道c的存在，也不知道自己的流量会不会阻塞c。

a是个自私的人，它选择时候不在乎别人的想法，但a是个聪明的人。

当a选择自己的x份流量流向某一路的时候，那么a知道自己其他路的流量就会减少x份。

a表示：“我自己不想管其他人，反正我这里随便分配自己的流量，别人要是因为我的流量被堵住了，那他们来借用我减少流量的路好了。”

以上面的例子来说，就是这个例子

当a先走e的时候，他知道自己c路将缺少流量，于是它决定建立反向的桥梁让其他路能够沿着这条路取借用自己的c边。

于是b再遍历的时候发现自己的d边被a占用了，虽然它很不爽，但是它只能沿着a架起的桥梁取走c的边。

事实上，当a走d的时候它也在借用d的容量，借用的数量取决于这条路上容量的最小值。

a说：“抱歉我用了你们的路，但是相反你们也能借用我的路，但是你们借用的不能超过我借用的！”

也就是a再建立反向边的同时设定反向边的容量等于该路的流量。

在上面的图中，虽然b的流量不足以填满a借用的，但是假如我再下面中间节点的底下再连上一条流，这条流也会借用反向边走b，一直到把a的借债填满为止。

这就是我自己对于最大流反向边建立算法的理解。

a在决定流的流入方向的同时，还不想阻塞其他流，所以它建立反向边允许其他流借用自己的边。这样，互相借用达成一种平衡，就是算法正确性的保证。

---

FF算法

FF算法就好像我们上面的人工过程，找到一个节点，从这个节点开始贪心填满与他相连的每一条边，用dfs同时建立反向边给予其他节点借用的机会，然后一点点算下去就行了。

wikipedia上面有python的代码，而且如果你自己想找代码的话我相信你也能找到合适的。

我这里贴上Wiki的代码

import collections

class Graph:
    """This class represents a directed graph using adjacency matrix representation."""

    def __init__(self, graph):
        self.graph = graph  # residual graph
        self.row = len(graph)

    def bfs(self, s, t, parent):
        """Returns true if there is a path from source 's' to sink 't' in
        residual graph. Also fills parent[] to store the path."""

        # Mark all the vertices as not visited
        visited = [False] * self.row

        # Create a queue for BFS
        queue = collections.deque()

        # Mark the source node as visited and enqueue it
        queue.append(s)
        visited[s] = True

        # Standard BFS loop
        while queue:
            u = queue.popleft()

            # Get all adjacent vertices of the dequeued vertex u
            # If an adjacent has not been visited, then mark it
            # visited and enqueue it
            for ind, val in enumerate(self.graph[u]):
                if (visited[ind] == False) and (val > 0):
                    queue.append(ind)
                    visited[ind] = True
                    parent[ind] = u

        # If we reached sink in BFS starting from source, then return
        # true, else false
        return visited[t]

    # Returns the maximum flow from s to t in the given graph
    def edmonds_karp(self, source, sink):

        # This array is filled by BFS and to store path
        parent = [-1] * self.row

        max_flow = 0  # There is no flow initially

        # Augment the flow while there is path from source to sink
        while self.bfs(source, sink, parent):

            # Find minimum residual capacity of the edges along the
            # path filled by BFS. Or we can say find the maximum flow
            # through the path found.
            path_flow = float("Inf")
            s = sink
            while s != source:
                path_flow = min(path_flow, self.graph[parent[s]][s])
                s = parent[s]

            # Add path flow to overall flow
            max_flow += path_flow

            # update residual capacities of the edges and reverse edges
            # along the path
            v = sink
            while v != source:
                u = parent[v]
                self.graph[u][v] -= path_flow
                self.graph[v][u] += path_flow
                v = parent[v]

        return max_flow

Dinic算法

之后的算法都是改进，如何才能更有效的算出结果。

Dinic算法在dfs基础上使用bfs将节点分层，分层后的节点保证算法不会兜圈子走远路。

Dinic算法会使用BFS不断更新节点的层数，便利的时候保证流向层次高的节点，而不是通过同层次的节点。

我很推荐大家去看Dinic算法的wikipedia，他下面有还算清晰的过程展示，至少比大多数文章要好。

如果你登不上wiki……

请看第一次bfs和dfs，主要到有些边算法目前还没有走，因为那些点处在同层次上，算法要求dfs必须走下一层次的节点。

有些边已经完全占满了，所以可以删掉他们了。

上一层中1->2的路6/8虽然有剩余，但是已经完全无法利用了，在bfs时候将他作为第3层次节点，而且该层次节点不能流入到t节点，它是无效的。

将上面的图占满的边删掉，bfs的时候只能走到1的那个节点了。

这个过程中你依旧能看到反向边的建立，但是似乎没怎么利用就是了。

---

至于Dinic算法的优化，如果你看一个算法首先先搞清处它优化在什么地方，那就本末倒置了。

顺便，如果你看不懂head数组和edge数组，去看图的链式前向星表示方法。

然后，每个节点都可能连着多个边，有些边连着下一层次的节点，他会在dfs中遍历到然后找到增广路，于是这条路之后就不需要再次遍历了，我们不断更新head数组中第一条边的位置就能实现弧优化了。

至于多路增广，我总感觉跟dfs差不多？这我还没完全看出来。

不过，太过注重优化有有些走偏了，算法——还是用来解决问题的呀。

---