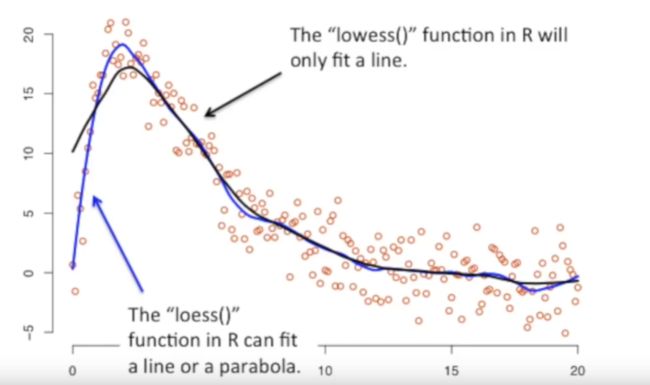
R -- loess函数
文章目录
- brief:
- Example
- 代码实例
- 用在时序数据上
brief:
通常我们使用最小二乘回归(OLS)去找到一条直线来最佳地拟合数据点,就像下面那样。
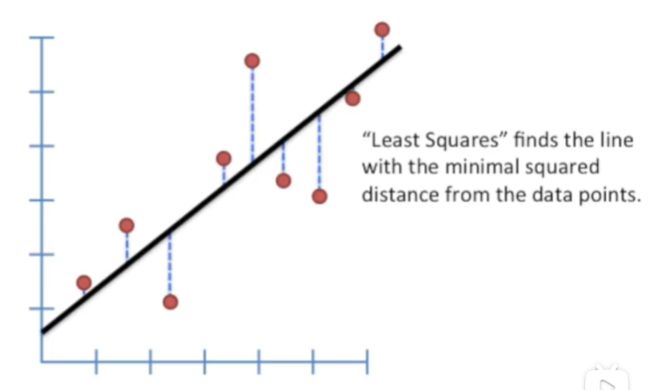
但是我们会遇到下面这种数据分布,我们应该怎样处理呢?广义线性回归 或者 Loess回归进行拟合?
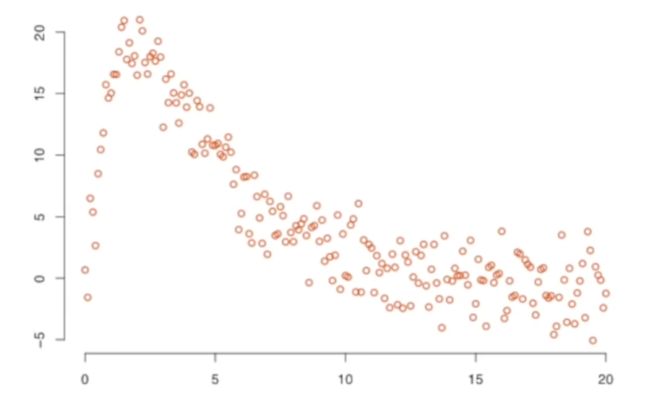
有人这样子想了,先把数据分段,然后每段数据内拟合,然后再连接拟合线,当你把数据分段约小,拟合线越平滑。
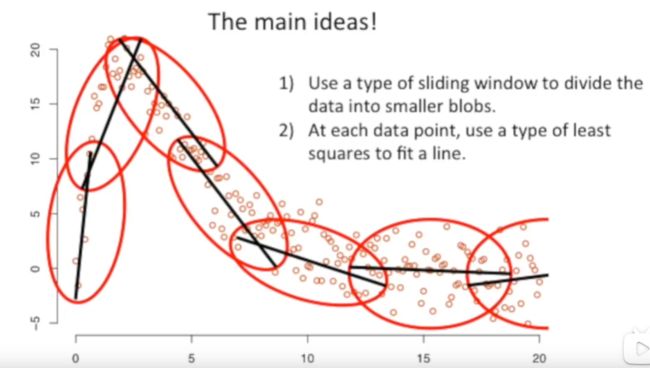
使用上面那种思想解决问题的办法就可以认为是loess回归。
接下来我们去看看一个简单的例子,了解下loess回归每一步做了什么?
Example
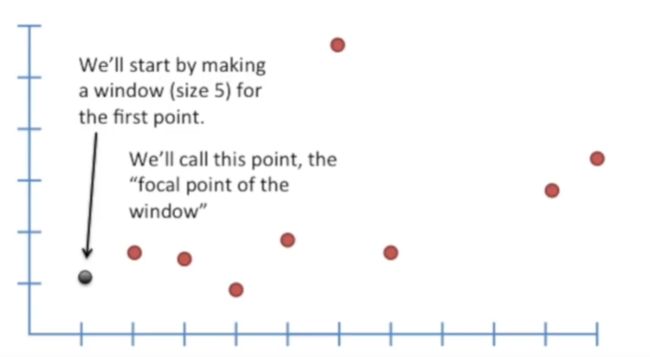
对于第一个数据点,称为 x,此时它是中心点。
然后计算离他最近的四个点(我们选取的windows = 5),进行线性拟合。
如果是OLS的话每个数据点的权重是一样的 ,但是现在进行拟合时我们要给每个数据点不一样的权重,使得 x的权重最大(这样就会出现x 对线性拟合的影响最大),距离 x 第一近的 数据点权重第二大,依此类推。
上述的加权回归结果就是 中心点 x 有一个回归预测值 Xpred。
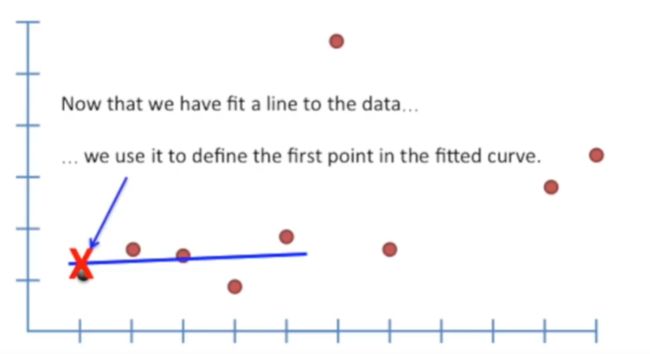
让我们一直对每一个数据点进行类似的加权回归,直到遇到下面这种情况,我们需要停下来,仔细检查一下:
图示中的 new point 用 X表示,也就是我们前述的 Xpred 偏离实际值太对,因为有个离他比较近的数据点出现了离群现象。
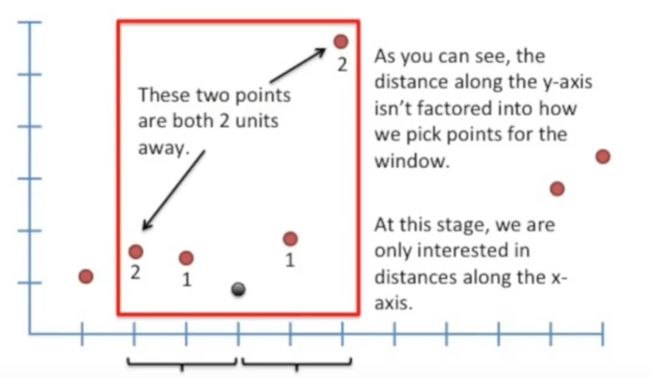

这个时候我们仅仅是检查,先不管上述问题,一直把所有数据点进行拟合:
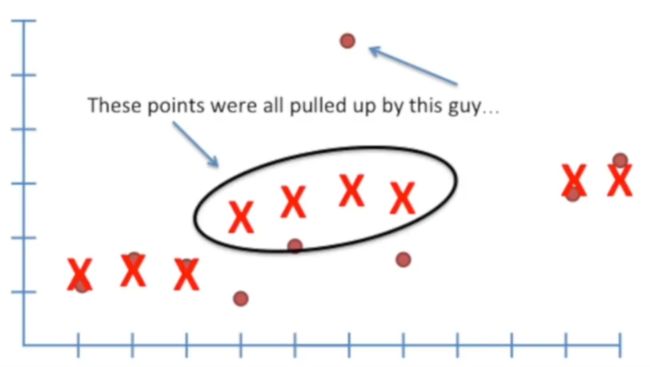
最后在解决上述离群点的问题:
第一次我们得到了一系列的Xpred,我们用Xpred作为数据点再次进行加权回归。
此时的权重等于x 与 Xpred的差值,x 与 Xpred距离远大,权重越小,x 与 Xpred距离越小权重越大。
所以我们得到了下面图示中的一系列Xpred,用红×表示。
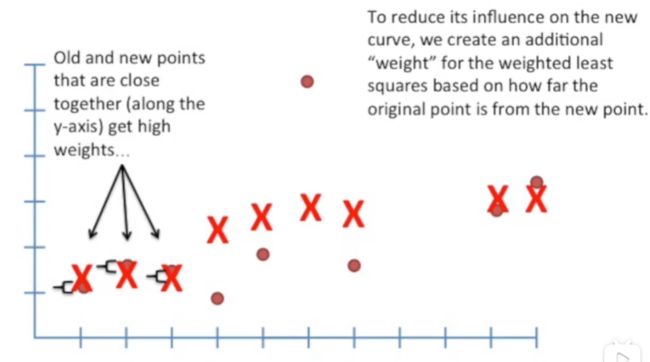
第二次加权拟合的结果:

代码实例
set.seed(123)
x <- seq(-5, 5, length.out = 100)
y <- exp(-x^2) + rnorm(length(x), sd = 0.1)
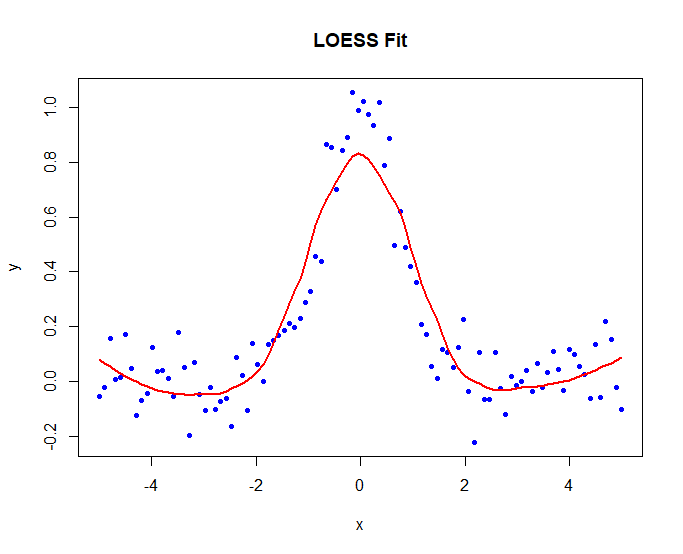
# 计算 LOESS 拟合曲线
fit <- loess(y ~ x, span = 0.5)
# 可视化数据和拟合曲线
plot(x, y, main = "LOESS Fit", pch = 20, col = "blue")
lines(x, predict(fit), col = "red", lwd = 2)
set.seed(123)
x <- seq(-5, 5, length.out = 100)
y <- exp(-x^2) + rnorm(length(x), sd = 0.1)
# 计算 LOESS 拟合曲线
fit <- loess(y ~ x, span = 0.1)
# 可视化数据和拟合曲线
plot(x, y, main = "LOESS Fit", pch = 20, col = "blue")
lines(x, predict(fit), col = "red", lwd = 2)
loess(formula, data, weights, subset, na.action, model = FALSE,
span = 0.75, enp.target, degree = 2,
parametric = FALSE, drop.square = FALSE, normalize = TRUE,
family = c(“gaussian”, “symmetric”),
method = c(“loess”, “model.frame”),
control = loess.control(…), …)
下面是几个比较重要的参数:

其中 span 控制 windows大小,小于1是表示windows占数据点的百分比,大于1表示windows包含所有数据点,
换句话说span 越接近于1拟合线越平滑,越接近0拟合线波动越大。
用在时序数据上
df <- read.csv("D:/603876.csv",header = T,row.names = 1,encoding = "UTF-8")
df <- df[,-1]
colnames(df) <- c("identity","date","open","close",
"high","low","volume","VOT","maplitude","U-D","VOU-D","turnover")
# 计算 LOESS 拟合曲线
trend <- loess(df$close ~ seq_along(df$close), span = 30/length(df$close))
# 可视化拟合曲线
plot(seq_along(df$close), df$close, main = "Data Trend", type = "l")
lines(seq_along(df$close), predict(trend), col = "red")
# 确定每个趋势的起点和终点
# 先让上涨的趋势数据点都为1,下降趋势的数据点都为0
trend_direction <- ifelse(diff(predict(trend)) >= 0, 1, 0)
# 趋势拐点则表现为差分不为0
trend_start <- c(1, which(diff(trend_direction) != 0)+1)
# 趋势开始的地方也是另一段趋势结束的地方
trend_end <- c(which(diff(trend_direction) != 0), length(trend_direction))
# 输出每个趋势的长度
for (i in seq_along(trend_start)) {
trend_length <- trend_end[i] - trend_start[i] + 1
trend_desc <- paste("Trend", i, "is", trend_direction[trend_start[i]], "with length of", trend_length)
print(trend_desc)
}