快速排序算法的编码和优化

快速排序的基本思路是：

1. 先通过第一趟排序，将数组原地划分为两部分，其中一部分的所有数据都小于另一部分的所有数据。原数组被划分为2份
2. 通过递归的处理， 再对原数组分割的两部分分别划分为两部分，同样是使得其中一部分的所有数据都小于另一部分的所有数据。 这个时候原数组被划分为了4份
3. 就1,2被划分后的最小单元子数组来看，它们仍然是无序的，但是！ 它们所组成的原数组却逐渐向有序的方向前进。
4. 到最后， 数组被划分为多个由一个元素或多个相同元素组成的单元， 这时候整个数组就有序了

总结： 通过第一趟排序，将原数组A分为B和C两部分， 整体上B从B1/B2/C1/C2的长度的单元看待整个数组， 从左至右 B1， 并且随着排序的深入，原数组有序性越来越强

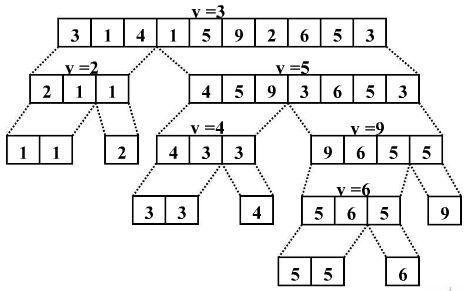
整体的排序过程如下图所示（暂且不管实现的具体细节）

如上图所示， 数组

3 1 4 1 5 9 2 6 5 3

复制

通过第一趟排序被分成了2 1 1 和4 5 9 3 6 5 3两个子数组，且对任意元素，左子数组总小于右子数组

通过不断递归处理，最终得到

1 1 2 3 3 4 5 5 6

复制

这个有序的数组

快排的实现步骤

快排具体的实现步骤如下图所示：

图中的步骤3，4不难理解，这里就不多赘述，因为步骤3中的递归思想是大家比较熟悉的， 步骤4中的“组合”其实就只是个概念上的词，因为所有的子数组本来就连接在一起，只要所有的递归结束了，整个数组就是有序的。

下面我就只讲解1和2步骤， 而在1,2中，关键在于如何实现“划分”

切分的关键点： 基准元素， 左游标和右游标

划分的过程有三个关键点：“基准元素”， “左游标” 和“右游标”。

• 基准元素：它是将数组划分为两个子数组的过程中， 用于界定大小的值， 以它为判断标准， 将小于它的数组元素“划分”到一个“小数值数组”里， 而将大于它的数组元素“划分”到一个“大数值数组”里面。这样，我们就将数组分割为两个子数组， 而其中一个子数组里的元素恒小于另一个子数组里的元素
• 左游标： 它一开始指向待分割数组最左侧的数组元素。在排序过程中，它将向右移动
• 右游标： 它一开始指向待分割数组最右侧的数组元素。在排序过程中，它将向左移动

【注意】

1.上面描述的基准元素/右游标/左游标都是针对单趟排序过程的， 也就是说，在整体排序过程的多趟排序中，各趟排序取得的基准元素/右游标/左游标一般都是不同的

2. 在不同的教材里，基准元素也叫“枢轴”，“关键字”， “划分”也叫“切分”

那这基准元素-右游标-左游标三个关键点是如何融会贯通，搞定一趟切分（划分）的呢？

一趟切分的具体过程

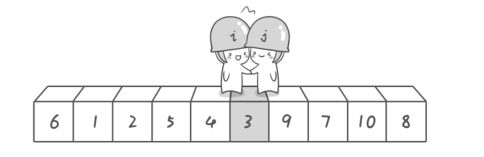
切分的具体过程如图所示。在下图中，基准元素是v,   左游标是i, 右游标是j

i一开始指向数组头部元素的位置lo, 切分时向右移动， j一开始指向数组末端元素hi,随后向左移动， 当左右游标相遇的时候，一趟切分就完成了。

当然， 看到这里你可能很懵懂，你可能会问：

• “基准元素v是怎么选的？”
• 游标i,j的移动的过程中发生了什么事情（比如元素交换）？，
• 为什么左右游标相遇时一趟切分就完成了？

让我们继续往下看：

基准元素的选取

首先，在原则上，基准元素的选取是任意的

但我们一般选取数组的第一个元素为基准元素（假设数组是随机分布的）

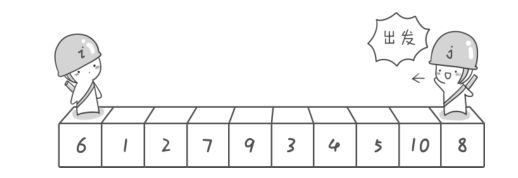
下面以啊哈磊老师的图示为例：

假设下面的是我们的待排序的数组的话， 根据我们的头元素作为基准元素的原则，士兵i下面的数组元素 “6” 就是我们选定的第一趟排序的基准元素

（作为入门，啊哈磊老师的《啊哈，算法》里的图示还是很有趣的！ 这里向大家安利一下）

【注意】下面在优化中会讲关于基准元素的选取的诀窍， 但在快排的基础编码里，我们只要记住把头部元素当作基准元素就够了（假设数组元素是随机分布的）

左右游标扫描和元素交换

在选取了基准元素之后， 切分就正式开始了。这时候，左右游标开始分别向右/左移动，它们遵循的规则分别是：

• 左游标向右扫描， 跨过所有小于基准元素的数组元素, 直到遇到一个大于或等于基准元素的数组元素， 在那个位置停下。
• 右游标向左扫描， 跨过所有大于基准元素的数组元素, 直到遇到一个大于或等于基准元素的数组元素，在那个位置停下

当左右游标扫描分两种情况（或者说是两个先后阶段...）

1. 左右游标没有相遇
2. 左右游标相遇了

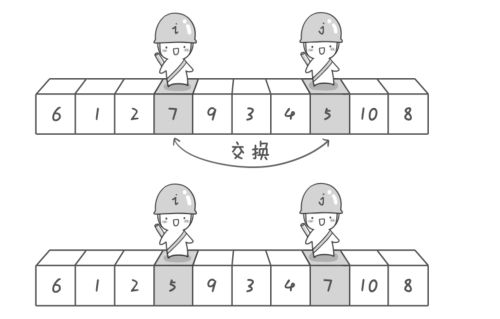
在下图中， 左游标就是士兵i, 而右游标是士兵j啦。

1.首先，右游标j会向左跨过所有大于基准元素的元素， 所以士兵j向左跨过了板砖8和10， 然后当他遇到了“小于等于”基准元素6的元素5时候， “哎呀， 不能再前进了，在这里打住吧！”， 于是右游标就在5处停了下来，

2.然后， 士兵i（左游标）跨过了小于基准元素6的1和2，然后遇到了“大于等于”6的7，在7处停了下来。

3.  停下来之后， 左右游标所指的数组元素交换了它们的值（两个士兵交换了他们脚下的板砖）

下图同上：

游标扫描和元素交换的意义

很明显， 两个游标士兵的“工作” 就是不断靠近，并检查有没有小于（大于）规定要求（即基准元素6）的板砖（元素），一旦发现， 就“丢”到对面去， 而当他们相遇的时候， 大小关系严格的两块子数组也就分割出来了

【注意】

1.要注意一点： 我们选取的基准元素和左游标最初指定的元素是相同的！ 那么就我们就会发现一个问题: 当左游标向右扫描的时候，第一个遇到的“大于或等于”的元素就是它本身， 那么问题来了： 需不需要停下来呢？ 当然根据逻辑思考可以得出这是不必要的，所以下面我会结合算法指出这一细节： 左游标向右扫描的时候其实忽略了它最初所指的位置——头元素的比较

2. 必须等一个“士兵”（游标）先走完， 另一个“士兵”（游标）才能走，不能每人轮流走一步...

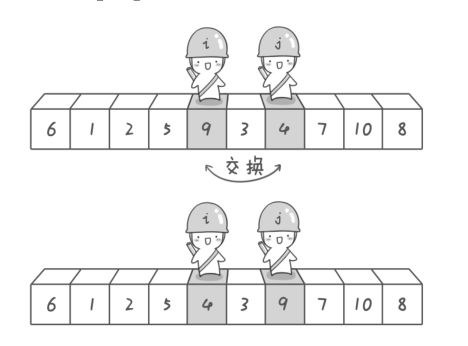
左右游标相遇

承接上文， 这次眼看士兵i和士兵j就要相遇了！ 首先士兵j先走，当它遇到3的位置的时候，因为3“小于等于”6，所以士兵j就停下来了。再然后士兵i向右走，但因为他和士兵j“碰头”了，所以士兵i只能无奈地“提前”在3停住了（如果没和j碰面士兵i是能走到9的!）

所以这就是左右游标扫描相遇时候遵循的原则： 只相遇， 不交叉

【注意】这里你可能会问： 在我们制定的规则里， 左游标先扫描和右游标先扫描有区别吗？ （如果你这样想的话就和我想到一块去了...嘿嘿），因为就上图而言,两种情况下一趟排序中两个游标相遇的位置是不同的（一般而言，除非相遇位置的下方的元素刚好和基准元素相同）：

• 如果右游标先扫描，左右游标相遇的位置应该是3上方（图示）
• 但如果左游标先扫描， 左右游标相遇的位置却是9上方

通过编码验证和翻阅书籍，我得出的结论是： 这对排序的划分过程有影响，但对最终结果是没有具体的影响的。特别的，在《数据结构》这本书中采取的是右游标先扫描，而在《算法（第四版）》书中，则采取左游标先扫描的策略

基准元素归位

当到达了我上面所说的“左右游标相遇”这个阶段后， 我们发现， 左右两个子数组已经基本有序了，即分成了 1 2 5 4 3和9 7 10 8 这两段元素，其中前一段元素都小于后一段元素

等等！ 好像有两个数字违和感很强地打破了这个大小关系， 那就是6！ （基准元素）

如下所示：

6 1 2 5 4 3 9 7 10 8

复制

这时候我们发现整个数组的组成是这样的： 大小居中的基准元素 + 小数值数组 + 大数值数组

所以我们只要把基准元素6和游标相遇元素3换一下， 不就可以变成： 小数值数组 + 大小居中的基准元素 +   大数值数组 了吗？

即

1 2 5 4 3 6 9 7 10 8

复制

如图所示

至此， 一趟排序结束， 回到中间的6已经处于有序状态，只要再对左右两边的元素进行递归处理就可以了

总结一趟排序的过程

OK，这里让我们总结下一趟快速排序的四个过程：

一趟排序全过程图示

（A - Z 字母排序， A最小， Z最大）

快速排序代码展示

具体的代码

这是我们的辅助函数exchange: 用于交换任意两个数组元素的位置：

// 交换两个数组元素
private static void exchange(int [] a , int i, int j) {
  int temp = a[i];
  a[i] = a[j];
  a[j] = temp;
}

复制

这是切分函数partition， 它完成了一轮排序的主要工作，使得待分割数组以基准元素为界，分成了一个小数值数组和一个大数值数组

private static int partition (int[] a, int low, int high) {
  int i = low, j = high+1; // i, j为左右扫描指针 PS： 思考下为什么j比i 多加一个1呢？
  int pivotkey = a[low];  // pivotkey 为选取的基准元素（头元素）
  while(true) { 
    while (a[--j]>pivotkey) {   if(j == low) break; }  // 右游标左移
    while(a[++i]=j) break;    // 左右游标相遇时候停止， 所以跳出外部while循环
    else exchange(a,i, j) ;  // 左右游标未相遇时停止, 交换各自所指元素，循环继续 
  }
  exchange(a, low, j); // 基准元素和游标相遇时所指元素交换，为最后一次交换
  return j;  // 一趟排序完成， 返回基准元素位置
}

复制

这是主体函数sort, 将partition递归处理

private static void sort (int [] a,  int low, int high) {
  if(high<= low) { return; } // 终止递归
  int j = partition(a, low, high);  // 调用partition进行切分
  sort(a,  low,  j-1);   // 对上一轮排序(切分)时，基准元素左边的子数组进行递归
  sort(a,  j+1,  high); // 对上一轮排序(切分)时，基准元素右边的子数组进行递归
}

复制

对切分函数partition的解读

1. 直观上看， partition由两部分组成： 外部while循环和两个并列的内部while循环。

2. 内部While循环的作用是使得左右游标相互靠近

例如对：

while (a[--j]>pivotkey) {  ...   }

复制

先将右游标左移一位，然后判断指向的数组元素和基准元素pivotkey比较大小， 如果该元素大于基准元素， 那么循环继续，j再次减1，右游标再次左移一位...... （循环体可以看作是空的）

3.外部While循环的作用是不断通过exchange使得“逆序”元素的互相交换， 不断向左子数组小于右子数组的趋势靠近， 

对

if(i>=j) break; 

复制

从i < j到 i == j 代表了“游标未相遇”到“游标相遇”的过度过程，此时跳出外部循环， 切分已接近完成，紧接着通过 exchange(a, low, j) 交换基准元素和相遇游标所指元素的位置， low是基准元素的位置（头部元素）, j是当前两个游标相遇的位置

4. 第一个内部while循环体里面的的  if(j == low) break；判断其实是多余的，可以去除。

因为在

while (a[--j]>pivotkey) {   if(j == low) break; }  // 右游标左移

复制

中，当随着右游标左移，到j = low + 1的时候，有 a[--j] == pivotkey为true（两者都是基准元素），自动跳出了while循环，所以就不需要在循环体里再判断 j == low 了

5. 注意一个细节： j 比 i 多加了一个1，为什么？ 如下

int i = low, j = high+1

复制

结合下面两个While循环中的判断条件：

while (a[--j]>pivotkey) {  ...   }
while (a[++i]

复制

可知道， 左游标 i 第一次自增的时候， 跳过了对基准元素 a[low] 所执行的 a[low] < pivotkey判断, 这是因为在我们当前的算法方案里，基准元素和左游标初始所指的元素是同一个，所以没有执行a[low]>pivotke这个判断的必要。所以跳过（ 一开始a[low] == pivotkey，如果执行判断那么一开始就会跳出内While循环，这显然不是我们希望看到的）

而相比之下，右游标却必须要对它初始位置所指的元素执行a[++i]

对主体函数sort的解读

1. high<= low是判断递归结束的条件

2. int j = partition(a, low, high);  有两种作用： 一是进行一轮切分， 二是取得上一轮的基准元素的最终位置j, 传递给另外两个sort函数，通过另外两个sort函数的调用

sort(a,  low,  j-1);  
sort(a,  j+1,  high);

复制

进行下一轮递归，设置j -1 和j + 1 是因为上一轮基准元素的位置已经是有序的了，不要再纳入下一轮递归里

快速排序QuickSort类的全部代码：

public class QuickSort {
  // 交换两个数组元素
  private static void exchange(int [] a , int i, int j) {
    int temp = a[i];
    a[i] = a[j];
    a[j] = temp;
  }
 
  private static int partition (int[] a, int low, int high) {
    int i = low, j = high+1;      // i, j为左右扫描指针 PS： 思考下为什么j比i 多加一个1呢？
    int pivotkey = a[low];  // pivotkey 为选取的基准元素（头元素）
    while(true) { 
      while (a[--j]>pivotkey) {   if(j == low) break; }  // 右游标左移
      while(a[++i]=j) break;    // 左右游标相遇时候停止， 所以跳出外部while循环
      else exchange(a,i, j) ;  // 左右游标未相遇时停止, 交换各自所指元素，循环继续 
    }
    exchange(a, low, j); // 基准元素和游标相遇时所指元素交换，为最后一次交换
    return j;  // 一趟排序完成， 返回基准元素位置
  }
 
  private static void sort (int [] a,  int low, int high) {
    if(high<= low) { return; } // 当high == low, 此时已是单元素子数组，自然有序， 故终止递归
    int j = partition(a, low, high);  // 调用partition进行切分
    sort(a,  low,  j-1);   // 对上一轮排序(切分)时，基准元素左边的子数组进行递归
    sort(a,  j+1,  high); // 对上一轮排序(切分)时，基准元素右边的子数组进行递归
  }
   
  public static void sort (int [] a){ //sort函数重载， 只向外暴露一个数组参数
    sort(a, 0, a.length - 1);
  }
}

复制

测试代码

public class Test {
  public static void main (String [] args) {
    int [] array = {4,1,5,9,2,6,5,6,1,8,0,7 };
    QuickSort.sort(array);
    for (int i = 0; i < array.length; i++) {
      System.out.print(array[i]);
    }
  }
}

复制

结果：

01124556789

复制

优化点一 —— 切换到插入排序

对于小数组而言， 快速排序比插入排序要慢， 所以在排序小数组时应该切换到插入排序。

只要把sort函数中的

if(high<= low) { return; }

复制

改成：

if(high<= low + M) {  Insertion.sort(a,low, high) return; } // Insertion表示一个插入排序类

复制

就可以了，这样的话，这条语句就具有了两个功能：

1. 在适当时候终止递归

2. 当数组长度小于M的时候（high-low <= M）， 不进行快排，而进行插排

转换参数M的最佳值和系统是相关的，一般来说， 5到15间的任意值在多数情况下都能令人满意

例如， 将sort函数改成：

  private static void sort (int [] a,  int low, int high) {
    if(high<= low + 10) {  Insertion.sort(a,low, high) return; } // Insertion表示一个插入排序类
    int j = partition(a, low, high);  // 调用partition进行切分
    sort(a,  low,  j-1);   // 对上一轮排序(切分)时，基准元素左边的子数组进行递归
    sort(a,  j+1,  high); // 对上一轮排序(切分)时，基准元素右边的子数组进行递归
  }

复制

优化点二 —— 基准元素选取的随机化

上面说过，基准元素的选取是任意的，但是不同的选取方式对排序性能的影响很大。

在上面所有的快速排序的例子中，我们都是固定选取基准元素，这种操作做了一个假设性的前提：数组元素的分布是随机的。而如果数组不是随机的，而是有一定顺序的，甚至在最坏的情况下:完全正序或完全逆序， 这个时候麻烦就来了： 快排所消耗的时间大大延长，完全达不到快排应有的效果。

所以为了保证快排算法的随机化，我们必须进行一些优化。

下面介绍的方法有三种：

1. 排序前打乱数组的顺序
2. 通过随机数保证取得的基准元素的随机性
3. 三数取中法取得基准元素（推荐）

1. 排序前打乱数组的顺序

public static void sort (int [] a){
  StdRandom.shuffle(a)  // 外部导入的乱序算法，打乱数组的分布
  sort(a, 0, a.length - 1);
}

复制

当然来了，因为乱序函数的运行，这会增加一部分耗时，但这可能是值得的

2.通过随机数保证取得的基准元素的随机性

  private static int getRandom (int []a, int low, int high) {
    int RdIndex = (int) (low + Math.random()* (high - low)); // 随机取出其中一个数组元素的下标
    exchange(a, RdIndex, low);  // 将其和最左边的元素互换
    return a[low];
  }
 
  private static int partition (int[] a, int low, int high) {
    int i = low, j = high+1;      // i, j为左右扫描指针 PS： 思考下为什么j比i 多加一个1呢？
    int pivotkey = getRandom (a, low, high); // 基准元素随机化
    while(true) { 
      while (a[--j]>pivotkey) {   if(j == low) break; }  // 右游标左移
      while(a[++i]=j) break;    // 左右游标相遇时候停止， 所以跳出外部while循环
      else exchange(a,i, j) ;  // 左右游标未相遇时停止, 交换各自所指元素，循环继续 
    }
    exchange(a, low, j); // 基准元素和游标相遇时所指元素交换，为最后一次交换
    return j;  // 一趟排序完成， 返回基准元素位置
  }

复制

3.  三数取中法（推荐）

一般认为， 当取得的基准元素是数组元素的中位数的时候，排序效果是最好的，但是要筛选出待排序数组的中位数的成本太高， 所以只能从待排序数组中选取一部分元素出来再取中位数， 经大量实验显示： 当筛选数组的长度为3时候，排序效果是比较好的， 所以由此发展出了三数取中法：

三数取中法： 分别取出数组的最左端元素，最右端元素和中间元素， 在这三个数中取出中位数，作为基准元素。

package mypackage;
 
public class QuickSort {
  // 交换两个数组元素
  private static void exchange(int [] a , int i, int j) {
    int temp = a[i];
    a[i] = a[j];
    a[j] = temp;
  }
 
  // 选取左中右三个元素，求出中位数， 放入数组最左边的a[low]中
  private static int selectMiddleOfThree(int[] a, int low, int high) {
    int middle = low + (high -  low)/2;  // 取得位于数组中间的元素middle
    if(a[low]>a[high])    { 
      exchange(a, low, high);  //此时有 a[low] < a[high]
    }
    if(a[middle]>a[high]){
      exchange(a, middle, high); //此时有 a[low], a[middle] < a[high]
    }
    if(a[middle]>a[low]) {
      exchange(a, middle, low); //此时有a[middle]< a[low] < a[high]
    }
    return a[low];  // a[low]的值已经被换成三数中的中位数， 将其返回
  }
 
  private static int partition (int[] a, int low, int high) {
    int i = low, j = high+1;      // i, j为左右扫描指针 PS： 思考下为什么j比i 多加一个1呢？
    int pivotkey = selectMiddleOfThree( a, low, high);
    while(true) { 
      while (a[--j]>pivotkey) {   if(j == low) break; }  // 右游标左移
      while(a[++i]=j) break;    // 左右游标相遇时候停止， 所以跳出外部while循环
      else exchange(a,i, j) ;  // 左右游标未相遇时停止, 交换各自所指元素，循环继续 
    }
    exchange(a, low, j); // 基准元素和游标相遇时所指元素交换，为最后一次交换
    return j;  // 一趟排序完成， 返回基准元素位置
  }
 
  private static void sort (int [] a,  int low, int high) {
    if(high<= low) { return; } // 当high == low, 此时已是单元素子数组，自然有序， 故终止递归
    int j = partition(a, low, high);  // 调用partition进行切分
    sort(a,  low,  j-1);   // 对上一轮排序(切分)时，基准元素左边的子数组进行递归
    sort(a,  j+1,  high); // 对上一轮排序(切分)时，基准元素右边的子数组进行递归
  }
   
  public static void sort (int [] a){ //sort函数重载， 只向外暴露一个数组参数
    sort(a, 0, a.length - 1);
  }
}

复制

优化点三 —— 去除不必要的边界检查

我在上面说过：“ 第一个内部while循环体里面的的  if(j == low) break；判断其实是多余的，可以去除”

（请把文章往上翻到标题—“对切分函数partition的解读”中的第4点）

那么， 能不能把另外一个边界检查  if(i == high) break; 也去除呢？ 当然是不能直接去除的，但是我们可以通过一些技巧使得我们能够去除它

首先要理解的是 if(i == high) break;的作用： 防止 i 增加到超过数组的上界， 造成数组越界的错误。

那么按照同样的思考方式，对于

while(a[++i]

复制

我们只要尝试把这一作用交给a[++i]

这里的技巧就是： 在排序前先把整个数组中最大的元素移到数组的最右边，这样的话， 就算左游标i增加（右移）到数组的最右端，a[++i]

代码：

public class QuickSort {
  // 交换两个数组元素
  private static void exchange(int [] a , int i, int j) {
    int temp = a[i];
    a[i] = a[j];
    a[j] = temp;
  }
 
  //将原数组里最大的元素移到最右边， 构造“哨兵”
  private static void Max(int [] a) {
    int max = 0;
    for(int i = 1; ia[max]) {
        max = i;
      }
    }
    exchange(a, max, a.length -1);
  }
 
  private static int partition (int[] a, int low, int high) {
    int i = low, j = high+1;      // i, j为左右扫描指针 PS： 思考下为什么j比i 多加一个1呢？
    int pivotkey = a[low];  // pivotkey 为选取的基准元素（头元素）
    while(true) { 
      while (a[--j]>pivotkey) {   }  // 空的循环体
      while(a[++i]=j) break;    // 左右游标相遇时候停止， 所以跳出外部while循环
      else exchange(a,i, j) ;  // 左右游标未相遇时停止, 交换各自所指元素，循环继续 
    }
    exchange(a, low, j); // 基准元素和游标相遇时所指元素交换，为最后一次交换
    return j;  // 一趟排序完成， 返回基准元素位置
  }
 
  private static void sort (int [] a,  int low, int high) {
    if(high<= low) { return; } // 当high == low, 此时已是单元素子数组，自然有序， 故终止递归
    int j = partition(a, low, high);  // 调用partition进行切分
    sort(a,  low,  j-1);   // 对上一轮排序(切分)时，基准元素左边的子数组进行递归
    sort(a,  j+1,  high); // 对上一轮排序(切分)时，基准元素右边的子数组进行递归
  }
   
  public static void sort (int [] a){ //sort函数重载， 只向外暴露一个数组参数
    Max(a); // 将原数组里最大元素移到最右边， 构造“哨兵”
    sort(a, 0, a.length - 1);
  }
}

复制

如果看到这里对“哨兵”这个概念还不是很清楚的话，看看下面这张图示：

《三种哨兵》

关于哨兵三再说几句： 在处理内部子数组的时候，右子数组中最左侧的元素可以作为左子数组右边界的哨兵（可能有点绕）

优化点四 —— 三切分快排（针对大量重复元素）

普通的快速排序还有一个缺点， 那就是会交换一些相同的元素

回忆一下我在前面提到的快排中对左右游标指定的规则：

• 左游标向右扫描， 跨过所有小于基准元素的数组元素, 直到遇到一个大于或等于基准元素的数组元素， 在那个位置停下。
• 右游标向左扫描， 跨过所有大于基准元素的数组元素，直到遇到一个大于或等于基准元素的数组元素，在那个位置挺停下

特别的， 当左右游标都指向和基准元素相同的元素时候， 不必要的交换就发生了

如图：

（下图中基准元素是6）

所以由此人们研究出了三切分快排（三路划分） ， 在左右游标的基础上，再增加了一个游标，用于处理和基准元素相同的元素

代码如下：

package mypackage;
 
public class Quick3way {
  public static void exchange(int [] a , int i, int j) {
    int temp = a[i];
    a[i] = a[j];
    a[j] = temp;
  }
 
  public static void sort (int [] a, int low, int high) {
    if(low>=high)  { return; }
    int lt = low, gt = high, i =low+1;
    int v = a[low];
    while(i<=gt) {
      int aValue = a[i];
      if(aValue>v) { exchange(a, i, gt--);  }
      else if(aValue

复制

切分轨迹：

（A - Z 字母排序， A最小， Z最大）