算法提高-搜索-DFS之剪枝与优化
DFS之剪枝与优化
- DFS之剪枝与优化
-
- AcWing 165. 小猫爬山
- AcWing 166. 数独
- AcWing 167. 木棒
- AcWing 168. 生日蛋糕
DFS之剪枝与优化
AcWing 165. 小猫爬山
DFS的五种剪枝方法
(1)优化搜索顺序
(2)排除等效冗余
(3)可行性剪枝
(4)最优性剪枝
(5)记忆化搜索(这个放在dp里面说了)
下面这题涉及三个剪枝
#include AcWing 166. 数独
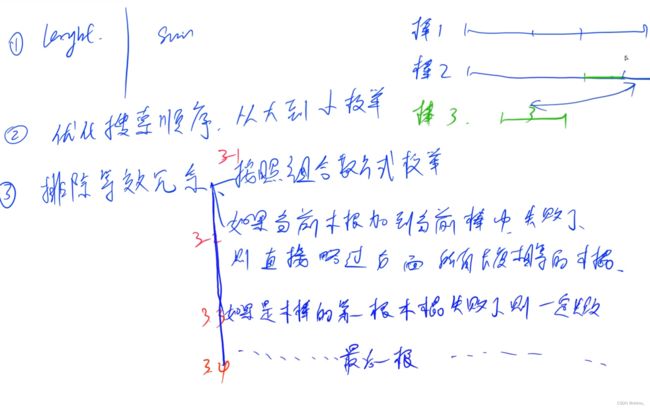
AcWing 167. 木棒
6种剪枝方法:1, 2, 3-1, 3-2, 3-3, 3-4
#include AcWing 168. 生日蛋糕
#include 