二叉树part7 | ● 530.二叉搜索树的最小绝对差 ● 501.二叉搜索树中的众数 ● 236. 二叉树的最近公共祖先

---

530.二叉搜索树的最小绝对差

530.二叉搜索树的最小绝对差

思路

题目中要求在二叉搜索树上任意两节点的差的绝对值的最小值。

注意是二叉搜索树，二叉搜索树可是有序的。

遇到在二叉搜索树上求什么最值啊，差值之类的，就把它想成在一个有序数组上求最值，求差值，这样就简单多了。
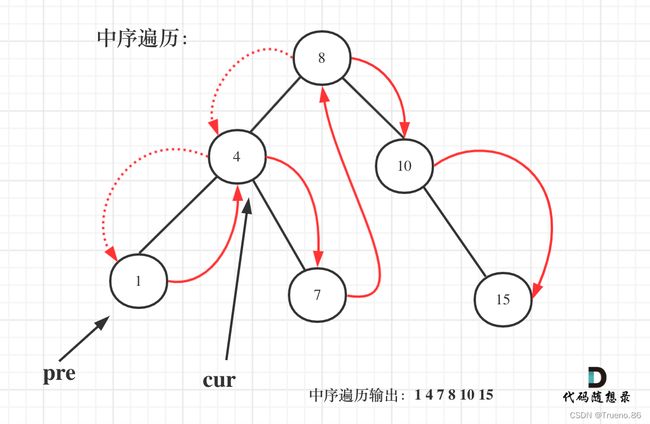
那么二叉搜索树采用中序遍历，其实就是一个有序数组。

在一个有序数组上求两个数最小差值，这是不是就是一道送分题了。

最直观的想法，就是把二叉搜索树转换成有序数组，然后遍历一遍数组，就统计出来最小差值了。
以上代码是把二叉搜索树转化为有序数组了，其实在二叉搜素树中序遍历的过程中，我们就可以直接计算了。

需要用一个pre节点记录一下cur节点的前一个节点。

时间复杂度On
空间复杂度On（递归调用栈深度）

代码

func getMinimumDifference(root *TreeNode) int {
    min:=100001
    pre:=(*TreeNode)(nil)
    var dfs func(*TreeNode)
    dfs = func(node *TreeNode){
        if node==nil{
            return
        }
        dfs(node.Left)
        if pre!=nil&&node.Val-pre.Val<min{
            min=node.Val-pre.Val
        }
        pre=node
        dfs(node.Right)
    }
    dfs(root)
    return min
}

困难

题目给出的是二叉搜索树，利用其特性。
学会在递归的过程中保存前一个节点的指针。

---

501.二叉搜索树中的众数

501.二叉搜索树中的众数

思路

二叉搜索树所以采用中序遍历，保存前一个节点的值，根据当前节点与前一个节点值相等与否判断次数。
时间复杂度On

官方题解

代码

func findMode(root *TreeNode) []int {
    res:=[]int{}
    var pre *TreeNode
    times,maxtimes:=1,0
    var dfs func(*TreeNode)
    dfs = func(node *TreeNode){
        if node==nil{
            return
        }
        dfs(node.Left)
        if pre!=nil&&node.Val==pre.Val{
            times++
        } else if pre!=nil{
            if times>maxtimes{
                res=[]int{pre.Val}
                maxtimes=times
            }else if times==maxtimes{
                res=append(res,pre.Val)
            }
            times=1
        }
        pre=node
        dfs(node.Right)
    }
    dfs(root)
    if times>maxtimes{
        res=[]int{pre.Val}
    }
    if times==maxtimes{
        res=append(res,pre.Val)
    }
    return res
}

困难

还要考虑最后一段相同数字的情况，所以在递归结束后还要根据递归外部的参数判断一次：

dfs(root)
    if times>maxtimes{
        res=[]int{pre.Val}
    }
    if times==maxtimes{
        res=append(res,pre.Val)
    }
    return res

---

236. 二叉树的最近公共祖先

236.二叉树的最近公共祖先

思路

遇到这个题目首先想的是要是能自底向上查找就好了，这样就可以找到公共祖先了。

那么二叉树如何可以自底向上查找呢？

回溯啊，二叉树回溯的过程就是从低到上。

后序遍历（左右中）就是天然的回溯过程，可以根据左右子树的返回值，来处理中节点的逻辑。

接下来就看如何判断一个节点是节点q和节点p的公共祖先呢。

首先最容易想到的一个情况：如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者 左子树出现结点q，右子树出现节点p，那么该节点就是节点p和q的最近公共祖先。

时间复杂度On

代码

func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
    if root==nil{
        return nil
    }
    if root==p||root==q{
        return root
    }
    left:=lowestCommonAncestor(root.Left, p, q)
    right:=lowestCommonAncestor(root.Right, p, q)
    if left!=nil&&right!=nil{
        return root
    }
    if left!=nil{
        return left
    }
    if right!=nil{
        return right
    }
    return nil
}

困难

使用递归回溯的思想，遍历一条边和遍历整棵树的区别。
如果递归函数有返回值，如何区分要搜索一条边，还是搜索整个树呢？

搜索一条边的写法：

if (递归函数(root->left)) return ;

if (递归函数(root->right)) return ;
搜索整个树写法：

left = 递归函数(root->left); // 左
right = 递归函数(root->right); // 右
left与right的逻辑处理; // 中
看出区别了没？

在递归函数有返回值的情况下：如果要搜索一条边，递归函数返回值不为空的时候，立刻返回，如果搜索整个树，直接用一个变量left、right接住返回值，这个left、right后序还有逻辑处理的需要，也就是后序遍历中处理中间节点的逻辑（也是回溯）。

---

今日收获

利用二叉搜索树（BST）的特性解题。
二叉树自底向上查找可以联想到回溯，后序遍历就是天然的回溯。
利用递归回溯，根据递归返回值判断解决问题。