Python 站点数据插值到格点 反距离权重插值 克里金法 径向基函数（RBF）插值

一、反距离权重插值

假设：彼此距离较近的事物要比彼此距离较远的事物更相似。当为任何未测量的位置预测值时，反距离权重法会采用预测位置周围的测量值与距离预测位置较远的测量值相比，距离预测位置最近的测量值对预测值的影响更大。反距离权重法假定每个测量点都有一种局部影响，而这种影响会随着距离的增大而减小。由于这种方法为距离预测位置最近的点分配的权重较大，而权重却作为距离的函数而减小，因此称之为反距离权重法。

1.1 库导入

import pandas as pd
import numpy as np
import geopandas as gpd
import netCDF4 as nc
import cartopy.crs as ccrs
import cartopy.feature as cfeat
from cartopy.mpl.ticker import LongitudeFormatter,LatitudeFormatter
import matplotlib.pyplot as plt
from matplotlib.image import imread
from cartopy.io.shapereader import Reader

1.2 站点观测数据

# 站点观测
data = pd.read_excel('weather_station_data.xlsx', 'Sheet1',  na_values=['NA'])
lon_sta = data['经度'][:].to_numpy()
lat_sta = data['纬度'][:].to_numpy()
t2m_sta = data['t2m_bilinear'][:].to_numpy()

1.3 半正矢公式（Haversine）计算球面两点的距离

#给定经纬度，计算地球上任意两点距离，单位m
import numpy as np
def haversine_dist(lon1,lat1,lon2,lat2):
  lon1,lat1,lon2,lat2 = map(np.radians, (lon1,lat1,lon2,lat2))
  radius = 6378.135E3 # radius of Earth, unit:m 
  dlat = lat2 - lat1
  dlon = lon2 - lon1
  arg = np.sin(dlat/2) ** 2 + np.cos(lat1) * np.cos(lat2) * np.sin(dlon/2) ** 2
  dist = 2 * radius * np.arcsin(np.sqrt(arg))
  return dist

1.4 IDW插值

def interp_IDW(lon_sta, lat_sta, data_sta, lon2D, lat2D):
    n_sta = len(lon_sta)
    ny, nx = np.shape(lon2D)
    data2D = np.zeros((ny, nx))
    for j in range(ny):
        for i in range(nx): #遍历二维每一个格点
            dist = [] # 格点至所有站点的距离
            for s in range(n_sta):
                d = haversine_dist(lon_sta[s], lat_sta[s], lon2D[j,i], lat2D[j,i])
                d = np.max([1.0, d])  # aviod divide by zero
                dist.append(d)
            wgt = 1.0 / np.power(dist, 2)
            wgt_sum = np.sum(wgt)
            arg_sum = np.sum(np.array(wgt) * np.array(data_sta))
            data2D[j,i] = arg_sum / wgt_sum
    return data2D

1.5 插值结果

# 插值的结果
t2m_IDW = interp_IDW(lon_sta, lat_sta, t2m_sta, lon2D, lat2D)

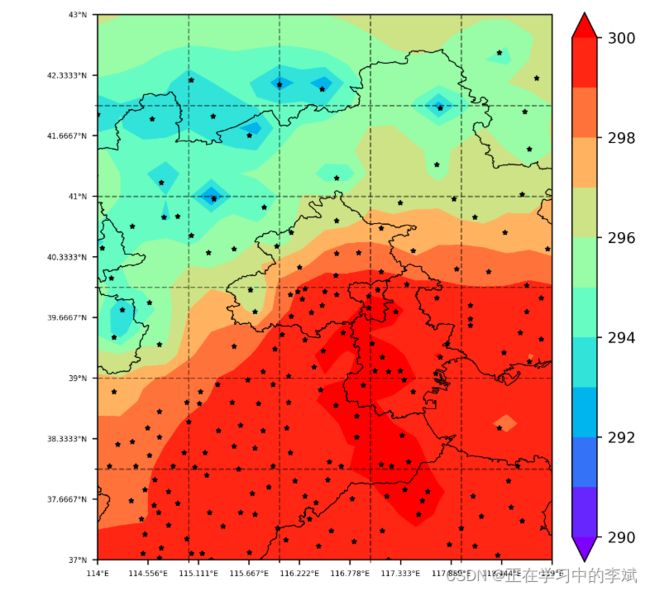
1.6 绘制反距离权重插值结果

# 绘制IDW插值结果
plot_contour_scatter(t2m_IDW, lon2D, lat2D, lon_sta, lat_sta, 't2m_IDW.png')

---

二、克里金法（Kriging）

Kriging是依据协方差函数对随机过程/随机场进行空间建模和预测（插值）的回归算法。在特定的随机过程，例如固有平稳过程中，克里金法能够给出最优线性无偏估计（Best Linear Unbiased Prediction, BLUP），因此在地统计学中也被称为空间最优无偏估计器(spatial BLUP)。克里金（kriging）插值是在有限区域内对区域化变量进行无偏最优估计的一种方法（用于估计在空间上有相关性的值，比如空气质量，相隔很近的位置的数值接近）。无偏指的是估计值和实际值之差的期望等于零，最优指的是估计值和实际值的方差最小。基于这一特点使得克里金插值的效果比其他插值方法要好很多。

普通克里金（Ordinary Kriging, OK） 泛克里金（Universal Kriging, UK） 协同克里金（Co-Kriging, CK） 析取克里金（Disjunctive Kriging, DK） 回归克里金（regression-Kriging） 神经网络克里金（neural Kriging） 贝叶斯克里金（Bayesian Kriging） 在Python里，有两个常用的克里金插值包，pykrige和pykriging。

总体而言，pykrige相对方便好用，支持普通克里金、泛克里金和回归克里金。

github网址：https://github.com/whdc/PyKrige

2.1 普通克里金用法，其他同理

 1. 构造 ordinary kriging object
 OK_obj  = OrdinaryKriging(lon_sta, lat_sta, t2m_sta, variogram_model="linear")
 输入：
 lon_sta: 站点经度，一维
 lat_sta: 站点纬度，一维
 t2m_sta：站点数据，一维，这里是温度
 参数：
 variogram_model：是变差函数模型，pykrige提供 linear, power, gaussian, spherical, 
                   exponential, hole-effect几种选择，默认的为linear模型。
 
 输出：
 OK_obj : 一个对象，pykrige.ok.OrdinaryKriging

2. 输出插值网格点的值
t2m_OK, ss = OK_obj.execute("grid", longitude, latitude) # 网格点处对应的值
输入：网格的经度和纬度，一维
输出：网格值和方差

2.2 普通克里金插值结果

from pykrige.ok import OrdinaryKriging

### 普通克里金（Ordinary Kriging, OK）
OK_obj = OrdinaryKriging(lon_sta, lat_sta, t2m_sta, variogram_model="linear")
# variogram_model是变差函数模型，
# pykrige提供 linear, power, gaussian, spherical, exponential, hole-effect几种选择，默认的为linear模型。
# 使用不同的variogram_model，插值效果是不一样的，应该针对自己的任务多尝试不同选项。

t2m_OK, ss = OK_obj.execute("grid", longitude, latitude) # 网格点处对应的值

2.3 泛克里金（Universal Kriging, UK）插值结果

# 泛克里金
from pykrige.uk import UniversalKriging
### 泛克里金（Universal Kriging, UK）
UK_obj = UniversalKriging(lon_sta, lat_sta, t2m_sta, variogram_model="linear")
t2m_UK, ss = UK_obj.execute("grid", longitude, latitude) # 给出网格点处对应的值

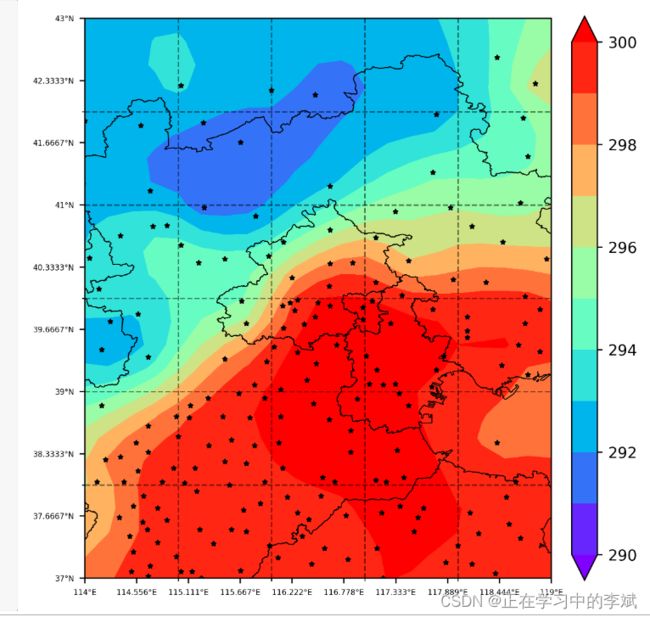
2.4 绘制普通克里金法插值结果

# 绘制克里金插值结果
plot_contour_scatter(t2m_OK, lon2D, lat2D, lon_sta, lat_sta, 't2m_OK.png')

---

三、径向基函数（RBF）插值

3.1 RBF方法是一系列精确插值方法的组合；即表面必须通过每一个测得的采样值。

有以下五种基函数：

1. 薄板样条函数
2. 张力样条函数
3. 规则样条函数
4. 高次曲面函数
5. 反高次曲面函数

3.2 RBF 插值结果

#  cubic, gaussian, inverse_multiquadric, linear, multiquadric, quintic, thin_plate
from scipy import  interpolate
func = interpolate.Rbf(lon_sta, lat_sta, t2m_sta, function='multiquadric')
t2m_RBF = func(lon2D,lat2D)#输入输出都是二维

3.3 绘制径向基函数（RBF）插值结果

# 绘制径向基函数插值结果
plot_contour_scatter(t2m_RBF, lon2D, lat2D, lon_sta, lat_sta, 't2m_RBF.png')

---

四、结果可视化和对比

4.1 导库

import xarray as xr
import salem
import numpy as np
import geopandas as gpd
import cartopy.crs as ccrs
import cartopy.feature as cfeat
from cartopy.mpl.ticker import LongitudeFormatter,LatitudeFormatter
import matplotlib.pyplot as plt
from matplotlib.cm import get_cmap
from matplotlib.image import imread
from cartopy.io.shapereader import Reader

4.2 验证数据

## ERA5 data，用于验证插值效果，并提供待插值的网格 lon2D，lat2D
## 北京地区2020年1，4，7，10月份（月平均）的地面数据
dataset = nc.Dataset("../data/ERA5_single_level_2020_1-4-7-10_beijing.nc")
print(dataset.variables.keys())
# 经纬度
longitude = dataset.variables['longitude'][:].data
latitude  = dataset.variables['latitude'][:].data
# 第2时次为7月份的数据
t2m_ERA5 = dataset.variables['t2m'][2].data

lon2D, lat2D = np.meshgrid(longitude,latitude)

4.3 定义通用方法

# 统一定制绘制方法

def plot_contour_scatter_subplot(data_list, data_name, lons2D, lats2D, lonSta, latSta, figname):
    lonMin = np.min(lons2D)
    lonMax = np.max(lons2D)
    latMin = np.min(lats2D)
    latMax = np.max(lats2D)
    
    proj = ccrs.PlateCarree() # 创建坐标系
    fig = plt.figure(figsize=(16, 18), dpi=400)  # 创建页面
    axes = fig.subplots(2,2, subplot_kw={'projection': proj})  # 创建子图
    rows = [0, 0, 1, 1]
    cols = [0, 1, 0, 1]
    for i in range(len(data_list)):
        ax = axes[rows[i], cols[i]]
        data2D = data_list[i]
        
        ax.set_extent([lonMin, lonMax, latMin, latMax])
        # --设置地图属性
        provinces = cfeat.ShapelyFeature(
            gpd.read_file('china_shp/province.shp')['geometry'],
            proj, 
            edgecolor='k',
            facecolor='none'
        )
        line = cfeat.ShapelyFeature(
            Reader('china_shp/nine_line.shp').geometries(),
            ccrs.PlateCarree(),
            edgecolor='k',
            facecolor='none'
        )
        ax.add_feature(provinces, linewidth=0.6, zorder=1)
        ax.add_feature(line, linewidth=0.6, zorder=1)
        ax.add_feature(cfeat.RIVERS.with_scale('110m'), linewidth=0.5, zorder=1)
        ax.add_feature(cfeat.LAKES.with_scale('110m'), linewidth=0.5, zorder=1)

        gl = ax.gridlines(
            crs = ccrs.PlateCarree(),
            draw_labels = False,
            linewidth = 0.9,
            color = 'k',
            alpha = 0.5,
            linestyle = '--'
        )
        gl.top_labels =  False  # 关闭经纬度标签
        gl.right_labels =False 
        # --设置刻度
        ax.set_xticks(np.linspace(int(lonMin), int(lonMax), num=5, endpoint=True))
        ax.set_yticks(np.linspace(int(latMin), int(latMax), num=5, endpoint=True))
        ax.xaxis.set_major_formatter(LongitudeFormatter())
        ax.xaxis.set_minor_locator(plt.MultipleLocator(1))
        ax.yaxis.set_major_formatter(LatitudeFormatter())
        ax.yaxis.set_minor_locator(plt.MultipleLocator(1))
        ax.tick_params(axis='both', labelsize=5, direction='out')

        levels = np.linspace(290.0, 300.0, 11, endpoint=True)
        ctr = ax.contourf(lons2D, lats2D, data2D,
                                 levels=levels,
                                 cmap=get_cmap("rainbow"),
                                 extend='both')
        
        cb = plt.colorbar(ctr, ax=ax, orientation="vertical", pad=.02, fraction=0.05)
        cb.ax.tick_params(labelsize=5)
        ax.set_title(data_name[i], {"fontsize" : 15})
        ax.scatter(
            lonSta,
            latSta,
            marker='*',
            s=8 ,
            color ="black"
        )
    plt.savefig(figname)
    return None

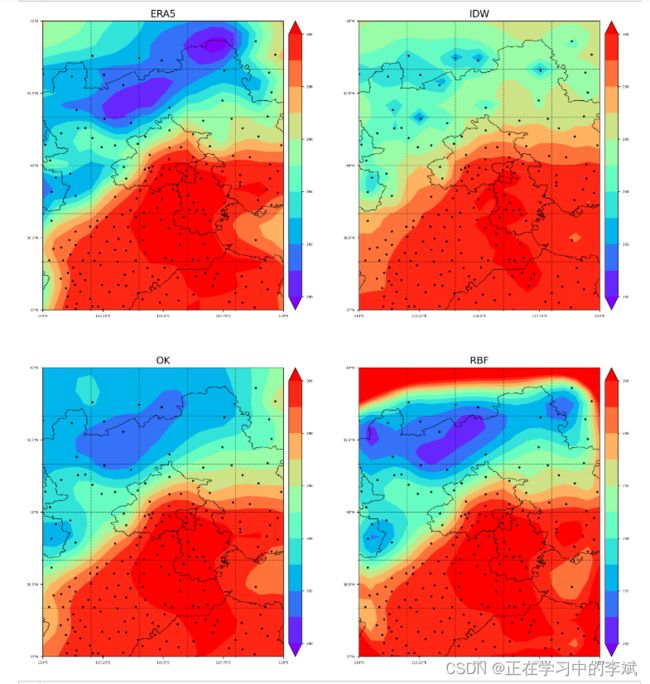
4.4 三种插值结果和验证数据对比

4.5 三种插值结果对比差异

diff_IDW = t2m_IDW - t2m_ERA5
diff_OK  = t2m_OK - t2m_ERA5
diff_RBF = t2m_RBF - t2m_ERA5
data_list = [diff_IDW, diff_OK, diff_RBF ]
data_name = ['IDW-ERA5', 'OK-ERA5', 'RBF-ERA5']
plot_contour_scatter_diff(data_list, data_name, lon2D, lat2D, lon_sta, lat_sta, 'diff_interp.png')