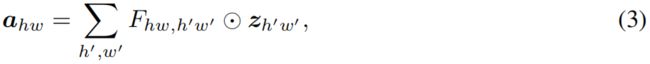GhostNet v2(NeurIPS 2022 Spotlight)原理与代码解析
paper:GhostNetV2: Enhance Cheap Operation with Long-Range Attention
code:https://github.com/huawei-noah/Efficient-AI-Backbones/tree/master/ghostnetv2_pytorch
背景
在智能手机和可穿戴设备上部署神经网络时,不仅要考虑模型的性能,还要考虑模型的效率,特别是实际推理速度。许多轻量模型比如MobileNet、ShuffleNet、GhostNet已经被应用到许多移动应用程序中。然而,基于卷积的轻量模型在长距离建模方面较弱,这限制了模型性能的进一步提升。Transformer引入的self-attention机制可以捕获全局信息,但是其复杂度相对于特征图的大小呈二次方的关系,对于计算非常不友好。此外,在计算attention map过程中还涉及大量的特征splitting和reshaping操作,虽然它们的理论复杂度可以忽略不计,但在实际应用中这些操作会产生更多的内存占用以及更长的延迟。
本文的创新点
本文提出了一种新的注意力机制(dubbed DFC attention)来捕获长距离的空间信息,同时保持了轻量型卷积神经网络的计算效率。为了简便只用了全连接层来生成atttention maps,具体来说,一个FC层被分解成了一个水平FC层和一个竖直FC层,这两个FC层沿各自的方向建模长距离的空间信息,结合这两个FC层就得到了全局的感受野。此外,作者重新研究了GhostNet中的bottleneck并加入了DFC attention来增强其中间层的特征表示,然后设计了一个新的轻量型骨干网络GhostNet v2,它可以在精度和推理速度之间获得更好的平衡。
方法介绍
A Brief Review of GhostNet
首先回顾下GhostNet,对于输入 \(X\in \mathbb{R}^{H\times W\times C}\),Ghost module将一个标准的卷积替换成两步。首先用一个1x1卷积生成intrinsic feature
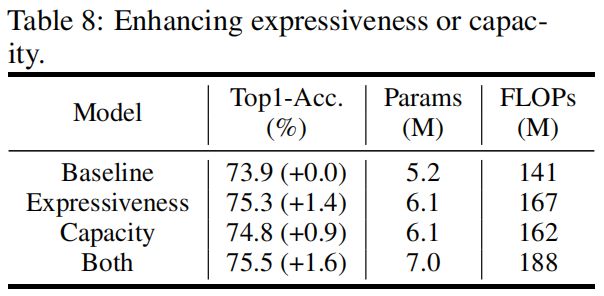
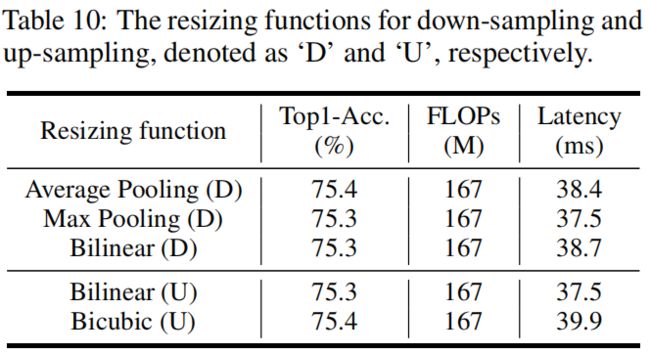
其中 \(*\) 表示卷积操作,\(F_{1\times 1}\) 是point-wise卷积,\(Y'\in \mathbb{R}^{H\times W\times C'_{out}}\) 是输出的intrinsic feature,它的通道数小于原始输出的通道数,即 \(C'_{out} 其中 \(F_{dp}\) 表示深度可分离卷积,\(Y\in \mathbb{R}^{H\times W\times C_{out}}\) 是输出特征。尽管Ghost module可以显著降低计算成本,但其表示能力也减弱了。空间像素之间的关系对准确识别至关重要,但在GhostNet中,空间信息只通过廉价操作(通常为3x3深度可分离卷积)作用于一半的特征来捕获,其余的特征通过1x1卷积生成,其中没有与空间其它像素的交互。由于捕获空间信息的能力较弱,阻碍了模型性能的进一步提升。 基于注意力的模型起源于NLP领域,最近被引入到计算机视觉领域,比如ViT、Non-local Networks等。通常注意力模块的复杂度相对于特征图的大小呈二次方的关系,因此不适用于需要高分辨率输入的目标检测、语义分割等下游任务。降低注意力模块复杂度的主流方法是将图像分割成多个窗口,在窗口内或交叉窗口内实现注意力操作,比如Swin Transformer、MobileViT等。但分割窗口和注意力的计算涉及到大量的reshaping和transposing操作,对于大模型增加的推理时间可以忽略不计,但对于轻量模型,增加的部署延迟不能忽略。 虽然self-attention可以很好地建模long-range dependence,但如上所述部署效率比较低。而全连接层也可以用于生成具有全局感受野的attention map,且更简单更容易实现。给定输入 \(Z\in \mathbb{R}^{H\times W\times C}\),可以把它看成 \(HW\) 个token \(z_{i}\in \mathbb{R}^{C}\),即 \(Z\in\left \{ z_{11},z_{12},...,z_{HW} \right \} \)。可以按试下直接用FC层来生成attention map 其中 \(\odot \) 表示element-wise mulplication,\(F\) 是全连接中的可学习权重,\(A=\left \{ a_{11},a_{12},...,a_{HW} \right \} \) 是生成的attention map。按上式计算比self-attention更简单,但计算量仍然是特征图大小的二次方关系,即 \(\mathcal{O}\left ( H^{2}W^{2} \right ) \),这里为了简便忽略通道 \(C\)。实际上,CNN中特征图通常是low-rank的,没有必要将不同位置的所有的输入输出token密集地连接起来,特征图2D形状的特点本身就提供了一种减少全连接层计算量的方法,即将式(3)沿水平和竖直方向分解成两个全连接层分别建模对应方向上的长距离特征,如下 对于原始输入 \(Z\),按顺序执行式(4)(5),就可以捕获两个方向上的long-range dependence。作者将这种操作称为解耦全连接注意力机制(decoupled fully connected attention, DFC),如下图所示 其复杂度为 \(\mathcal{O}\left ( H^{2}W+HW^{2} \right ) \)。在式(3)的full attention中,对于一个方形区域内的某个像素位置,区域内所有像素点都直接参与该点注意力的计算。在DFC attention中,一个像素位置所在的行和列中的所有像素都直接参与该点注意力的计算,所以该区域内所有像素位置也都间接参与该点注意力的计算。 通过共享部分权重,式(4)(5)可以通过卷积来实现,从而避免影响实际推理速度的reshaping和transposing操作。对于输入特征依次执行大小为 \(1\times K_{H}\) 和 \(K_{W}\times 1\) 的深度可分离卷积,其复杂度变为 \(\mathcal{O}\left ( K_{H}HW+K_{W}HW \right ) \)。 作者基于GhostNet v1加入了DFC attention增强其表示能力,提出了GhostNet v2。 输入 \(X\in\mathbb{R}^{H\times W\times C}\) 分别送入两个分支,一个是原始的Ghost module按式(1)(2)生成输出特征 \(Y\),另一个分支是DFC module按式(4)(5)生成attention map \(A\),对于输入 \(X\) 先用一个1x1卷积将其转换成DFC的输入 \(Z\),最终的输出 \(O\in\mathbb{R}^{H\times W\times C}\) 是两个分支输出的乘积 信息聚合的过程如下图所示 由于原始的Ghost module即式(1)(2)的操作是非常高效的,直接将DFC与其并行会带来额外的计算成本。因此通过分别沿水平和竖直方向降采样来减小特征图的大小,这样DFC中的所有操作都可以在较小的特征图上进行。这里默认水平和竖直方向分别降采样一半,这样DFC中的总FLOPs就减小了75%。然后再上采样将其还原为原始大小,从而和Ghost分支保持一致。这里下采样和上采样分别采用平均池化和双线性插值。注意这里的sigmoid函数也是作用在下采样后的特征图上的,虽然上采样后其值不是严格的在 \((0,1)\) 区间内,但作者发现这对最终性能的影响可以忽略不计。 GhostNet采用了包含两个Ghost module的inverted residual bottleneck的结构,其中第一个module生成通道数更多的expand feature,第二个module减少通道数生成output feature。作者通过实验发现将DFC作用于第一个module模型性能更高,因此最终只将DFC attention与expand feature相乘。GhostV2 bottleneck的结构如下图所示 作为一个通用的module,DFC可以嵌入其它模型中,作者将DFC嵌入MobileNetV2中,并和其它注意力module进行对比,包括SE、CBAM、CA,结果如下,可以看出DFC取得了最高的精度。 作者根据特征图大小将GhostNetV2分为3个stage,并对比了每个阶段不同kernel size对最终精度的影响,结果如下,可以看出增大kernel size可以更大范围的信息,并进一步提高精度。 作者比较了将DFC放到模型不同位置对最终精度的影响,结果如下,可以看出将其放到任一个stage中都可以提升精度,默认情况下,所有层中都加入DFC。 对于一个attention map,需要将其值归一化到\((0,1)\)区间中,作者对比了将sigmoid放到不同位置对精度的影响,结果如下,可以看到将其放到上采样之前,虽然经过插值后attention map中的值不是严格的处于\((0,1)\)区间内,但对最终精度影响不大,并且可以降低延迟。因此默认设置下,将sigmoid置于上采样之前。 如前所述,一个bottleneck包含两个Ghost module,第一个负责升维增强expressiveness,第二个负责降维增强capacity,作者比较了将DFC atttention放到不同module中的精度差异,如下图所示,可以看到将DFC放到第一个module中用来增强expressiveness精度更高,虽然两个module中都放置DFC精度更高,但计算量也随之增大,因此默认设置下,只在第一个module中加入DFC attention。 作者对比了下采样和上采样的不同方法,结果如下,可以看到GhostNetV2对resizing方法的选择比较鲁棒,不同的方法最终的精度差异不大。因为下采样中max pooling的延迟最低,上采样中bilinear的延迟更低,因此默认设置下分别采用max pooling和bilinear插值。 BottleneckV2的代码如下,可以看出只在第一个ghost module即self.ghost1中使用DFC attention。另外这里的实现和文章中有出入,上面的消融实验中提到在所有的层中都加入DFC attention,但下面的实现中前两层即layer_id <= 1时没加入DFC。 GhostModuleV2的代码如下,其中self.short_conv就是DFC分支,首先avg pooling进行下采样,这里和文章也不一样,文中消融实验中提到max pooling的延迟低因此默认采用max pool。然后经过1x1卷积,接着是horizontal FC和vertical FC,这里用卷积替代两个方向的FC卷积核大小为(1, 5)、(5, 1),最终经过sigmoid得到DFC分支的输出。DFC分支的输出经过bilinear插值上采样得到原始输入大小,然后与原始ghost module的输出相乘得到最终输出。Revisit Attention for Mobile Architecture
DFC Attention for Mobile Architecture
GhostNet v2
Enhancing Ghost module
Feature downsampling
GhostV2 bottleneck
实验结果
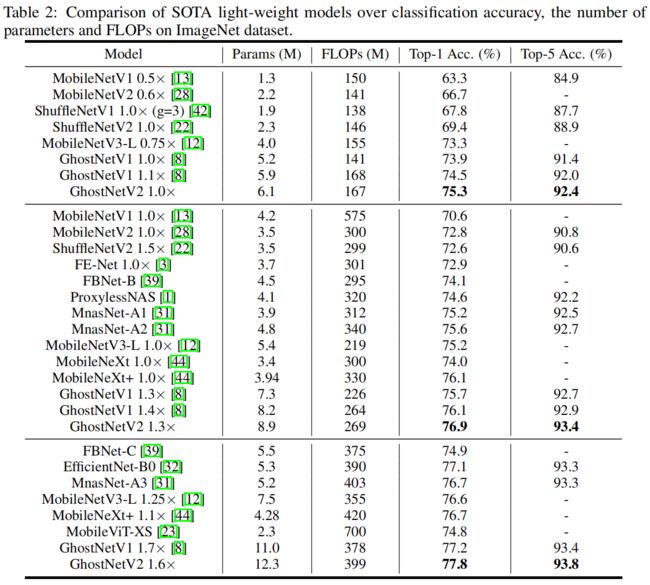
Image Classification on ImageNet
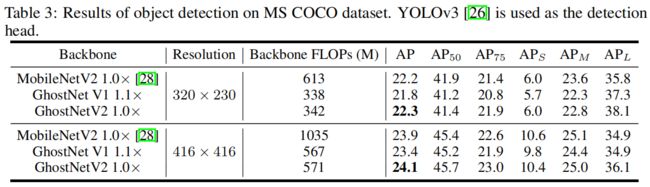
Object Detection on COCO
Semantic Segmentation on ADE20K
消融实验
Experiments with other models.
The impact of kernel size in DFC attention.
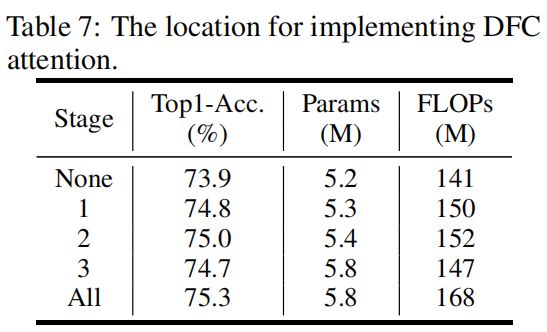
The location for implementing DFC attention.
The impact of scaling function.
Enhancing expressiveness or capacity.
The resizing functions for up-sampling and down-sampling.
代码解析
class GhostBottleneckV2(nn.Module):
def __init__(self, in_chs, mid_chs, out_chs, dw_kernel_size=3,
stride=1, act_layer=nn.ReLU, se_ratio=0.,layer_id=None,args=None):
super(GhostBottleneckV2, self).__init__()
has_se = se_ratio is not None and se_ratio > 0.
self.stride = stride
# Point-wise expansion
if layer_id<=1:
self.ghost1 = GhostModuleV2(in_chs, mid_chs, relu=True,mode='original',args=args)
else:
self.ghost1 = GhostModuleV2(in_chs, mid_chs, relu=True,mode='attn',args=args)
# Depth-wise convolution
if self.stride > 1:
self.conv_dw = nn.Conv2d(mid_chs, mid_chs, dw_kernel_size, stride=stride,
padding=(dw_kernel_size-1)//2,groups=mid_chs, bias=False)
self.bn_dw = nn.BatchNorm2d(mid_chs)
# Squeeze-and-excitation
if has_se:
self.se = SqueezeExcite(mid_chs, se_ratio=se_ratio)
else:
self.se = None
self.ghost2 = GhostModuleV2(mid_chs, out_chs, relu=False,mode='original',args=args)
# shortcut
if (in_chs == out_chs and self.stride == 1):
self.shortcut = nn.Sequential()
else:
self.shortcut = nn.Sequential(
nn.Conv2d(in_chs, in_chs, dw_kernel_size, stride=stride,
padding=(dw_kernel_size-1)//2, groups=in_chs, bias=False),
nn.BatchNorm2d(in_chs),
nn.Conv2d(in_chs, out_chs, 1, stride=1, padding=0, bias=False),
nn.BatchNorm2d(out_chs),
)
def forward(self, x):
residual = x
x = self.ghost1(x)
if self.stride > 1:
x = self.conv_dw(x)
x = self.bn_dw(x)
if self.se is not None:
x = self.se(x)
x = self.ghost2(x)
x += self.shortcut(residual)
return xclass GhostModuleV2(nn.Module):
def __init__(self, inp, oup, kernel_size=1, ratio=2, dw_size=3, stride=1, relu=True, mode=None, args=None):
super(GhostModuleV2, self).__init__()
self.mode = mode
self.gate_fn = nn.Sigmoid()
if self.mode in ['original']:
self.oup = oup
init_channels = math.ceil(oup / ratio)
new_channels = init_channels * (ratio - 1)
self.primary_conv = nn.Sequential(
nn.Conv2d(inp, init_channels, kernel_size, stride, kernel_size // 2, bias=False),
nn.BatchNorm2d(init_channels),
nn.ReLU(inplace=True) if relu else nn.Sequential(),
)
self.cheap_operation = nn.Sequential(
nn.Conv2d(init_channels, new_channels, dw_size, 1, dw_size // 2, groups=init_channels, bias=False),
nn.BatchNorm2d(new_channels),
nn.ReLU(inplace=True) if relu else nn.Sequential(),
)
elif self.mode in ['attn']:
self.oup = oup
init_channels = math.ceil(oup / ratio)
new_channels = init_channels * (ratio - 1)
self.primary_conv = nn.Sequential(
nn.Conv2d(inp, init_channels, kernel_size, stride, kernel_size // 2, bias=False),
nn.BatchNorm2d(init_channels),
nn.ReLU(inplace=True) if relu else nn.Sequential(),
)
self.cheap_operation = nn.Sequential(
nn.Conv2d(init_channels, new_channels, dw_size, 1, dw_size // 2, groups=init_channels, bias=False),
nn.BatchNorm2d(new_channels),
nn.ReLU(inplace=True) if relu else nn.Sequential(),
)
self.short_conv = nn.Sequential(
nn.Conv2d(inp, oup, kernel_size, stride, kernel_size // 2, bias=False),
nn.BatchNorm2d(oup),
nn.Conv2d(oup, oup, kernel_size=(1, 5), stride=1, padding=(0, 2), groups=oup, bias=False),
nn.BatchNorm2d(oup),
nn.Conv2d(oup, oup, kernel_size=(5, 1), stride=1, padding=(2, 0), groups=oup, bias=False),
nn.BatchNorm2d(oup),
)
def forward(self, x):
if self.mode in ['original']:
x1 = self.primary_conv(x)
x2 = self.cheap_operation(x1)
out = torch.cat([x1, x2], dim=1)
return out[:, :self.oup, :, :]
elif self.mode in ['attn']:
res = self.short_conv(F.avg_pool2d(x, kernel_size=2, stride=2))
x1 = self.primary_conv(x)
x2 = self.cheap_operation(x1)
out = torch.cat([x1, x2], dim=1)
return out[:, :self.oup, :, :] * F.interpolate(self.gate_fn(res), size=(out.shape[-2], out.shape[-1]),
mode='nearest')