【Leetcode】贪心 区间问题 | 用最小数量的箭引爆气球、无重叠区间、划分字母区间、合并区间

452 用最少数量的箭引爆气球

更像一个重叠区间问题，贪心策略：应该在重叠最多处射出。

按区间左端点递增序进行排序，左端点相同时，按右端点递增序排序。

现在欲射穿气球$i$，当发现相邻的两个区间有重叠时，重叠部分为$[star{t}_{i+1},\min \{en{d}_i,en{d}_{i+1}\}]$，此时至少可以一箭双雕。

所以策略为：不断判断当前重叠区间是否与下一个区间相交，(1) 若相交，可将下一个区间加入，一同射穿，同时更新当前重叠区间。(2) 不相交，需要一支新的箭，更新count，转向判断下一个区间。

注意：一个不太好de的bug，Comparator里不能直接写o1[0] - o2[0]，而应该使用比较运算符判断，否则可能会溢出。

import java.util.Arrays;
import java.util.Comparator;

class Solution {
    public int findMinArrowShots(int[][] points) {
        int n = points.length;

        Arrays.sort(points, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                if (o1[0] != o2[0]) {
                    return o1[0] < o2[0] ? -1 : 1;
                }
                return o1[1] < o2[1] ? -1 : 1;
            }
        });

        // 开始时射出一枚箭
        int count = 1;
        int[] overlap = points[0];

        for (int i = 1; i < n; i++) {
            // 当前区间和overlap区间有重叠
            if (overlap[1] >= points[i][0]) {
                // 因为左端点递增，所以新的左端点一定来自下一个区间，新的右端点通过比较得到
                overlap = new int[]{points[i][0], Math.min(overlap[1], points[i][1])};
            }
            else {
                // 与overlap区间没有重叠，需要多射出一枚弓箭
                count++;
                overlap = points[i];
            }
        }

        return count;
    }
}

435 无重叠区间

贪心策略：选择可加入区间中，右端点最小的区间。

实现方法：按照右端点优先排序，右端点相同时，左端点更大优先。

[2,4]
[3,4] √

• 维护变量$rightBorder$，表示区间的左边界应大于等于$rightBorder$。

• 如果左端点大于等于当前右边界，说明没有重叠，可以加入，$count$增加，并更新$rightBorder$。

import java.util.Arrays;
import java.util.Comparator;

class Solution {
    public int eraseOverlapIntervals(int[][] intervals) {
        // 更小的右端点优先，右端点相同时，更大的左端点优先
        Arrays.sort(intervals, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                if (o1[0] == o2[0] && o1[1] == o2[1]) {
                    return 0;
                }
                if (o1[1] != o2[1]) {
                    return o1[1] < o2[1] ? -1 : 1;
                }
                return o1[0] < o2[0] ? 1 : -1;
            }
        });

        int count = 1;
        int rightBorder = intervals[0][1];

        for (int i = 1; i < intervals.length; i++) {
            // 如果左端点大于等于当前右边界，说明没有重叠，可以加入
            if (intervals[i][0] >= rightBorder) {
                count++;
                rightBorder = intervals[i][1];
            }
        }

        return intervals.length - count;
    }
}

463 划分字母区间

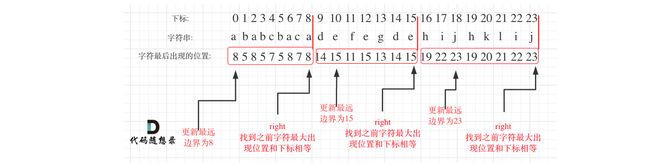
1. 统计每一个字符最后出现的位置
2. 从头遍历字符，记录所有字符的最远出现下标$border$，如果字符的下标与最远出现下标相等，则找到了分割点。

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;

class Solution {
    public List<Integer> partitionLabels(String s) {
        
        HashMap<Character, Integer> farthest = new HashMap<>();

        char[] word = s.toCharArray();

        for (int i = 0; i < word.length; i++) {
            farthest.put(word[i], i);
        }

        int border = -1;
        int count = 0;
        List<Integer> res = new ArrayList<>();

        for (int i = 0; i < word.length; i++) {
            // 先更新border
            border = Math.max(border, farthest.get(word[i]));
            count++;
            // 再检查下标是否和border相等
            if (i == border) {
                res.add(count);
                count = 0;
            }
        }

        return res;
    }
}

56 合并区间

按照左端点递增序排序，左端点相同时，按照右端点递减序排序。

遍历区间：

• 如果当前区间的左端点小于等于右边界，说明当前区间有重叠，可以合并，更新右边界为二者中的更大值

  [1,4], [2,3]
  overlap[1] = Math.max(overlap[1], intervals[i][1]);
  

• 否则说明没有重叠，将重叠区间$overlap$加入结果集，并更新$overlap$为当前区间。

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;

public class Solution {
    public int[][] merge(int[][] intervals) {
        // 按照左端点递增，右端点递减序排序
        Arrays.sort(intervals, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                if (o1[0] == o2[0] && o1[1] == o2[1]) {
                    return 0;
                }
                if (o1[0] != o2[0]) {
                    return o1[0] < o2[0] ? -1 : 1;
                }
                return o1[1] < o2[1] ? -1 : 1;
            }
        });

        ArrayList<int[]> merged = new ArrayList<>();
        int[] overlap = intervals[0];

        for (int i = 1; i < intervals.length; i++) {
            // 如果有重叠，可以合并
            if (overlap[1] >= intervals[i][0]) {
                overlap[1] = Math.max(overlap[1], intervals[i][1]);
            }
            else {
                merged.add(overlap);
                overlap = intervals[i];
            }
        }

        merged.add(overlap);

        return merged.toArray(new int[merged.size()][]);
    }
}