二叉搜索树
人生没有太晚的开始,所有的时刻都是七点。 —— 温妮 · 普赖弗曼
作者:不能再留遗憾了
专栏:Java学习
本文章主要内容:明解什么是二叉搜索树以及二叉搜索树的递归和非递归查找、插入和删除。
文章目录
- 什么是二叉搜索树
- 二叉搜索树的查找
- 构建二叉搜索树(插入数据)
- 二叉搜索树的删除
- 总结
什么是二叉搜索树
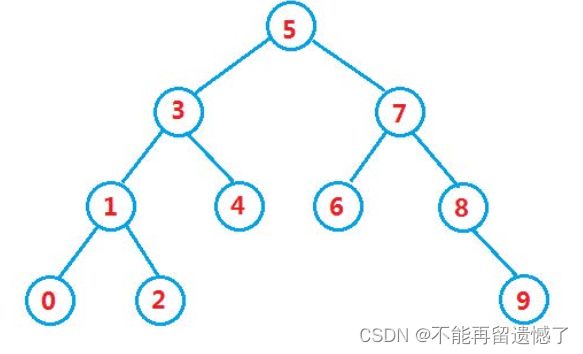
二叉搜索树(Binary Search Tree,也叫做BST)是一种常见的二叉树,但是它具有普通二叉树不具备的性质:
1.对于每个节点,他的左子树中所有节点的键值小于它的键值,而右子树中的所有节点的键值大于它的键值。
2.没有键值相同的节点。(因为二叉搜索树的主要作用是搜索查找数据,而不是存储数据)
二叉搜索树的查找
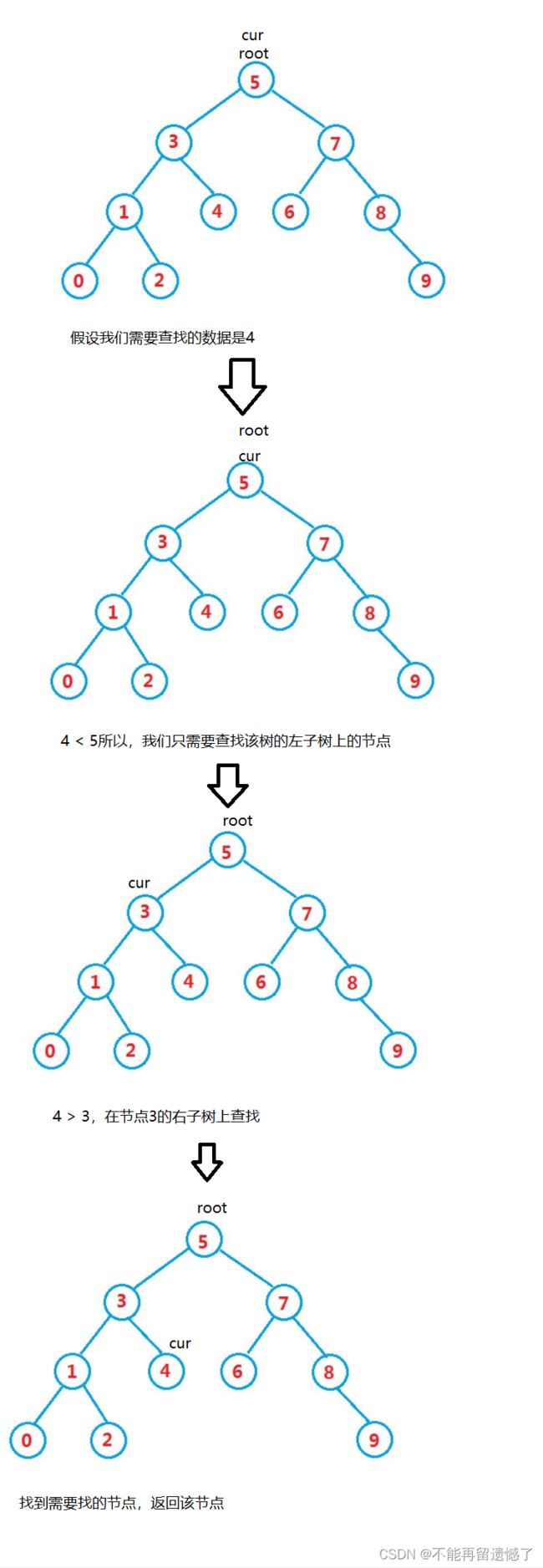
因为二叉搜索树的节点的键值大于左子树所有节点的键值,小于于右子树所有结点的所有的键值。所以我们在查找的时候至少可以少找一个子树,这就大大降低了时间的消耗。我们在查找的时候只需要比较要查找的数据的节点键值的大小,如果大于节点的键值,那么就在该节点的右子树上找,小于就在左子树上找,重复该操作,直到找到需要的值,返回该节点,没找到就返回null。
非递归查找
public class BinarySearchTree {
//我们创建一个树内部类,包含键值和左右子树
static class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
public TreeNode root = null;
//查找
public TreeNode find(int val) {
TreeNode cur = root;
while(cur != null) {
if(cur.val == val) {
return cur;
}else if(cur.val > val) {
cur = cur.left;
}else {
cur = cur.right;
}
}
return null;
}
}
递归查找
public class BinarySearchTree {
static class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
public TreeNode root = null;
//查找
public TreeNode find(int val) {
TreeNode cur = root;
return findChild(cur,val);
}
//递归查找
private TreeNode findChild(TreeNode cur,int val) {
if(cur == null) {
return null;
}
if(cur.val == val) {
return cur;
}else if(val > cur.val) {
cur = findChild(cur.right,val);
}else {
cur = findChild(cur.left,val);
}
return cur;
}
构建二叉搜索树(插入数据)
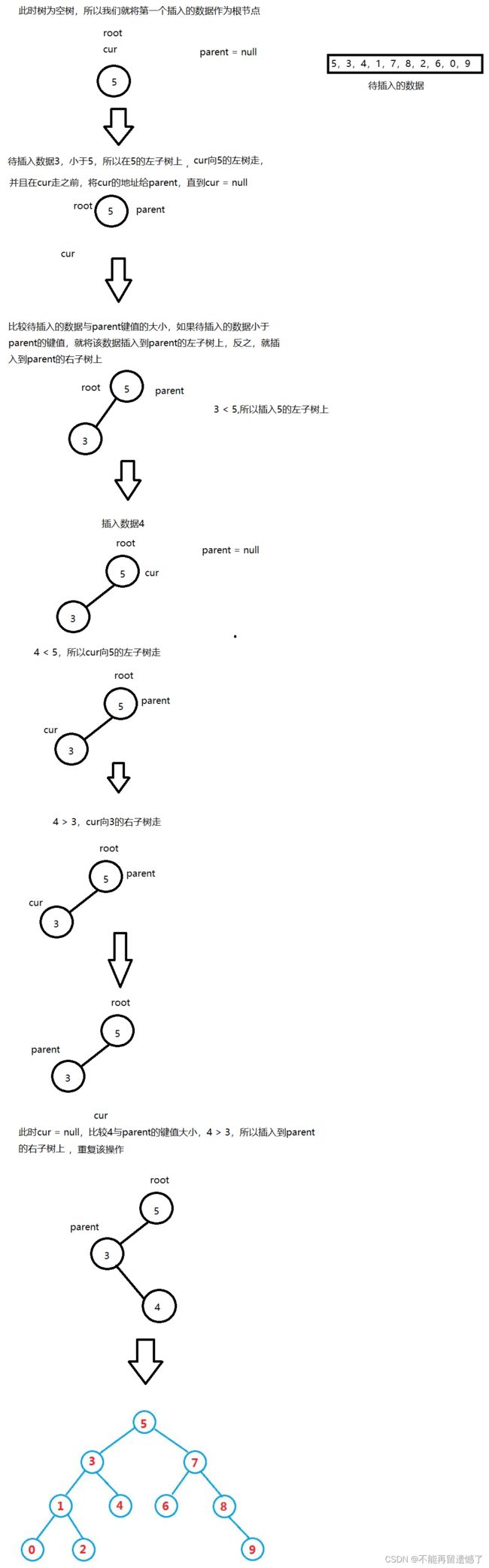
当一开始二叉树为空树时,我们第一个插入的数据,或者我们可以选取一个数据,要求这个数据的左子树的键值都小于它,右子树的键值都大于它,将这个数据作为二叉搜索树的根节点。
当二叉搜索树中存在节点的时候,我们再插入数据的时候就需要判断待插入的数据与节点的键值的关系了,如果待插入的数据小于节点的键值,那么说明待插入的数据一定在该节点的左子树上,如果待插入的数据大于节点的键值,那么待插入的数据就一定插在该节点的右子树上。并且我们不难发现:我们新插入的节点总是插在树的树叶上。所以当我们的遍历节点cur到达null时就判断待插入的数据与cur的父亲节点parent的关系,然后将新节点插入到parent的左子树或者右子树。
非递归插入
public void insert(int val) {
//判断再插入数据之前该树是否为空树
if(root == null) {
root = new TreeNode(val);
return;
}
TreeNode cur = root;
//我们需要记住cur的父亲节点,方便将cur与parent连接
TreeNode parent = null;
while(cur != null) {
if(cur.val > val) {
parent = cur;
cur = cur.left;
}else if(cur.val < val) {
parent = cur;
cur = cur.right;
}else {
//这种是相等的情况,因为二叉搜索树中不存在相同的键值,所以我们直接返回
return;
}
}
//这里我们判断是插入到parent的左子树上还是右子树上
if(val > parent.val) {
parent.right = new TreeNode(val);
}else {
parent.left = new TreeNode(val);
}
}
递归插入
public void insert(int val) {
//当插入之前树为空树时,将待插入数据作为树的根节点
if(root == null) {
root = new TreeNode(val);
return;
}
TreeNode parent = null;
TreeNode cur = root;
insertChild(parent,cur,val);
}
public void insertChild(TreeNode parent,TreeNode cur,int val) {
if(cur == null) {
if (parent.val < val) {
parent.right = new TreeNode(val);
return;
} else if (parent.val > val) {
parent.left = new TreeNode(val);
return;
} else {
return;
}
}
if(cur.val > val) {
insertChild(cur,cur.left,val);
}else if(cur.val < val){
insertChild(cur,cur.right,val);
}else {
return;
}
}
二叉搜索树的删除
俗话说:“请神容易,送神难”。我们往二叉搜索树中插入数据很简单,但是要是想删除数据,那可就不简单了,不像数组,数组删除数据只需要将要删除的数据的后面的一个一个向前覆盖就行了。但是二叉搜索树可没那么容易,因为你删除数据之后既要保证它是一个二叉树,还要保证它是二叉搜索树,不能破坏二叉搜索树的结构。
如果想要删除数据,我们需要分情况讨论:1.要删除的节点的左子树为空时。2.要删除的节点的右子树为空时。3.要删除的节点的左右子树都不为空时。前两种情况相对于左右子树都不为空这种情况较简单,我们先来看看前两种情况该怎么做。
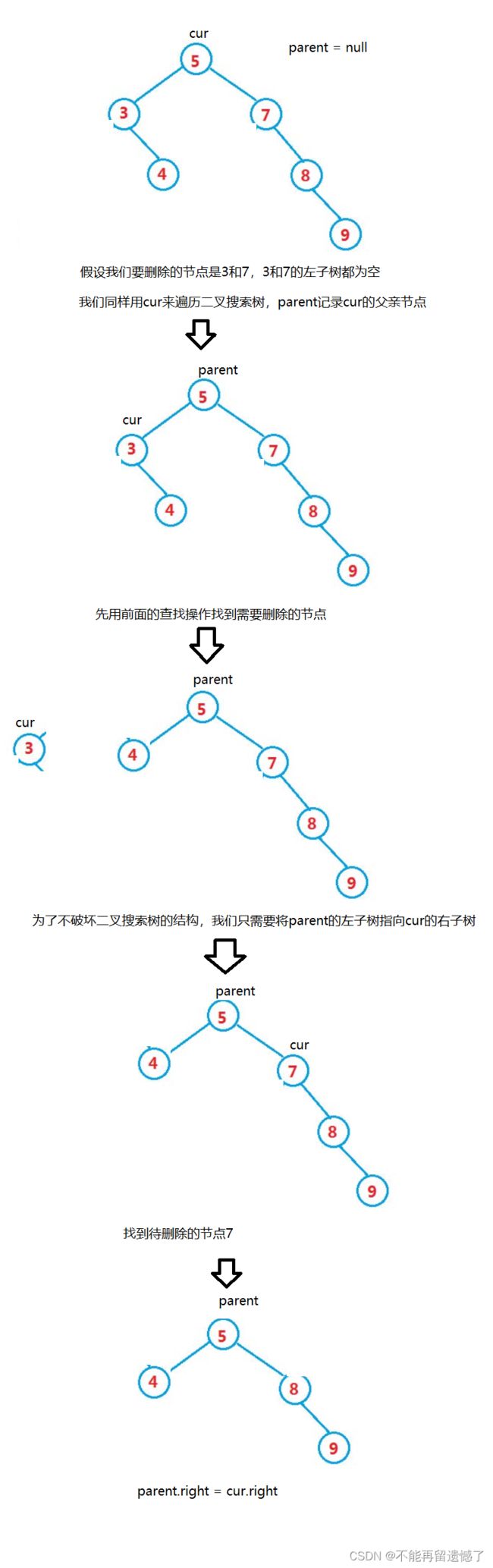
当左子树或者右子树为空时
当右子树为空时,操作跟左子树为空类似,只是需要判断待删除的节点是在parent的左子树上还是右子树上。并且还有一种特殊情况,当待删除的节点为root根节点时,我们只需要将root变化一下就行了。
public void revome(int val) {
TreeNode cur = root;
TreeNode parent = null;
//找到待删除的节点
while(cur != null) {
if(cur.val > val) {
parent = cur;
cur = cur.left;
}else if(cur.val < val) {
parent = cur;
cur = cur.right;
}else {
//删除节点
removeChild(parent,cur);
}
}
}
private void removeChild(TreeNode parent,TreeNode cur) {
if(cur.left == null) {
//当cur = null时
if(cur == root) {
root = root.right;
}else if(parent.left == cur) {
parent.left = cur.right;
}else {
parent.right = cur.right;
}
}else if(cur.right == null) {
if(cur == root) {
root = root.right;
}else if(parent.left == cur) {
parent.left = cur.left;
}else {
parent.right = cur.left;
}
}
}
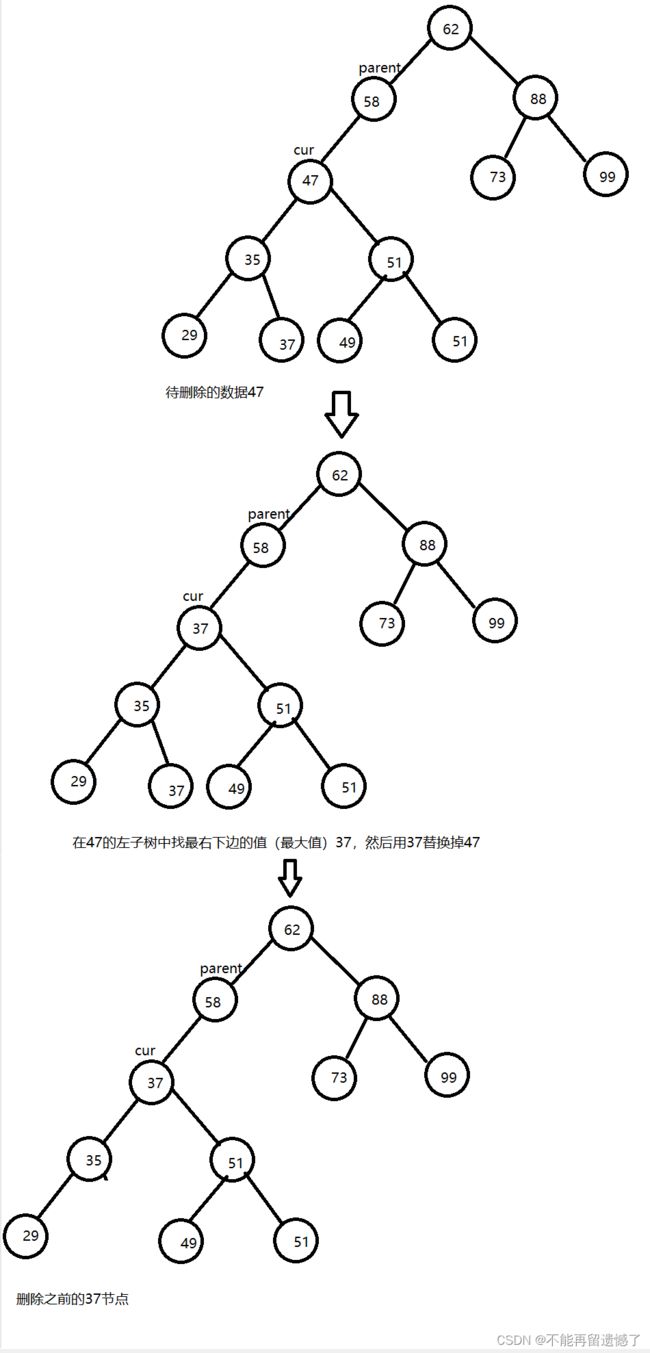
当左子树和右子树都不为空时
当待删除的节点的左右子树都不能空时,我们可以用该节点的左子树的最右边的节点(左子树的键值最大的节点)或者右子树最左边的节点(右子树键值最小的节点)取代这个待删除的节点,然后再删除这个节点。为什么要选择这两个节点呢?因为这两个节点的键值与待删除的节点的键值最相近,选取这两个数据替代待删除的数据不会破坏二叉搜索树的结构。
//在右子树中找最小节点
TreeNode targetP = cur;
TreeNode target = cur.right;
while(target.left != null) {
targetP = target;
target = target.left;
}
cur.val = target.val;
if(targetP.left == target) {
targetP.left = target.right;
}else {
targetP.right = target.right;
}
}
删除操作整体代码
public void revome(int val) {
TreeNode cur = root;
TreeNode parent = null;
while(cur != null) {
if(cur.val > val) {
parent = cur;
cur = cur.left;
}else if(cur.val < val) {
parent = cur;
cur = cur.right;
}else {
removeChild(parent,cur);
}
}
}
private void removeChild(TreeNode parent,TreeNode cur) {
if(cur.left == null) {
if(cur == root) {
root = root.right;
}else if(parent.left == cur) {
parent.left = cur.right;
}else {
parent.right = cur.right;
}
}else if(cur.right == null) {
if(cur == root) {
root = root.right;
}else if(parent.left == cur) {
parent.left = cur.left;
}else {
parent.right = cur.left;
}
}else {
TreeNode targetP = cur;
TreeNode target = cur.right;
while(target.left != null) {
targetP = target;
target = target.left;
}
cur.val = target.val;
if(targetP.left == target) {
targetP.left = target.right;
}else {
targetP.right = target.right;
}
}
}
总结
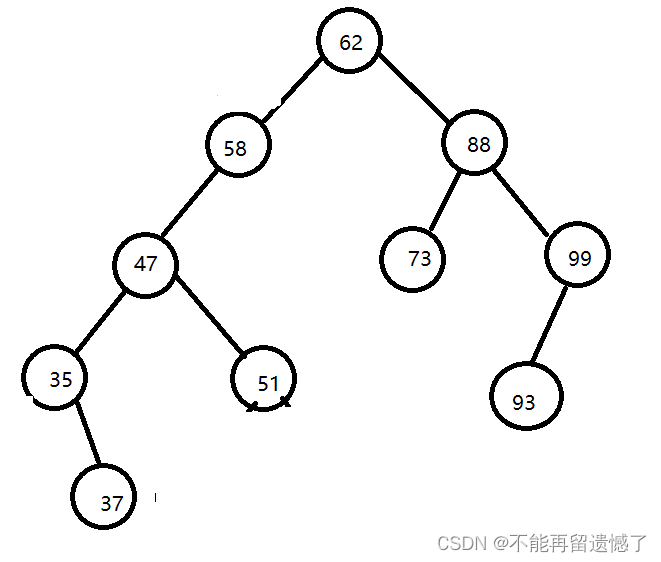
总之,二叉排序树以链接的方式存储,保持了链接存储结构在执行插入或删除操作时不用移动元素的优点,只要找到合适的插入和删除位置后,仅需修改链接指针即可。插入删除的时间性能比较好。而对于二叉排序树的查找,走的就是从根结点到要查找的结点的路径,其比较次数等于给定值的结点在二叉排序树中的层数。极端情况,最少为1次,即根结点就是要找的结点,最多也不会超过树的深度。也就是说,二叉排序树的查找性能取决于二叉排序树的形状。可问题就在于,二叉排序树的形状是不确定的。
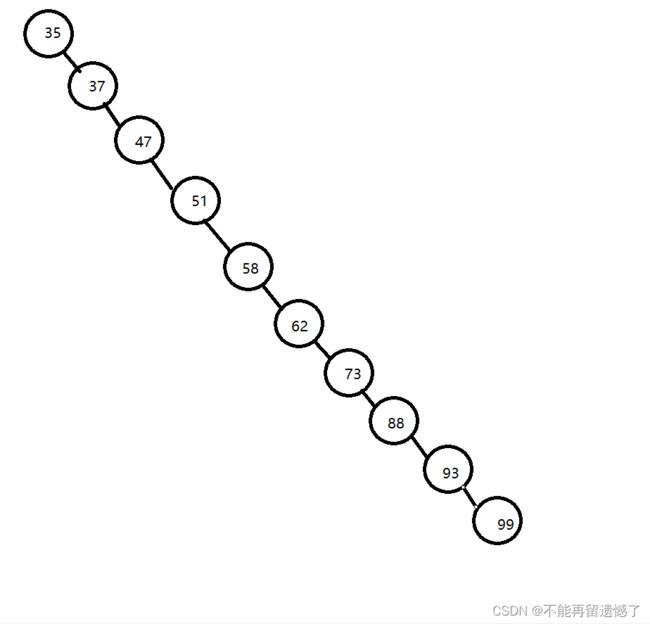
例如{62,88,58,47,35,73,51,99,37,93}这样的数组,我们可以构建如下图1所示的二叉排序树。但如果数组元素的次序是从小到大有序,如{35,37,47,51,58,62,73,88,93,99},则二叉排序树就成了极端的右斜树,注意它依然是一棵二叉排序树,如下图2。此时,同样是查找结点99,下图1只需要两次比较,而下图2就需要10次比较才可以得到结果,二者差异很大。