循环队列(Ring Buffer)

背景： 最近在复习数据结构和算法，顺带刷刷题，虽然很长时间不刷题了但还是原来熟悉的味道，每一次重学都是加深了上一次的理解。本次我们看一下 循环队列(Ring Buffer)，C语言实现。

循环队列：首先 它是一个队列，实现的功能就是 先进先出，后进后出，FIFO (First In First Out) ，而所谓的" 循环队列 " 其 实就是 将 队列 首尾相接来实现 队列的功能，为什么要首尾相接呢？ 或者说 首尾相接 有什么好处，或 解决了什么问题？

1. 队列 

首先说 队列，这个数据结构底层是由数组或链表组成， 由数组构成的队列称为 “顺序队列”，由链表实现的队列称为“链式队列”。类似于初高中时候， 在食堂的窗口进行排队打饭，挨着窗口的同学是 队首， 最后一个同学是队尾，按照先来后到的顺序，你需要排在最后一个同学的后面。

一般情况下，我们都会使用“顺序队列”来实现，因为数组比链表在某些方面更加高效。

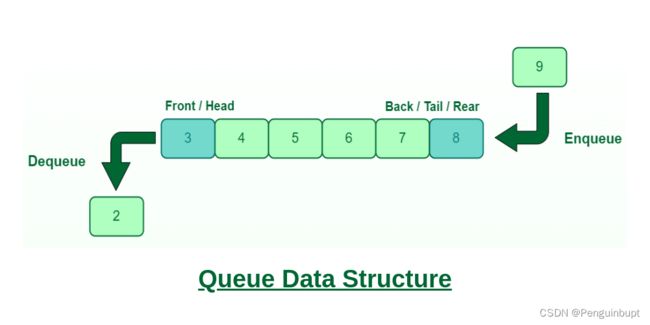
顺序队列如下图所示：

 顺序队列是一个数组， 对它的操作有 入队和出队，然后判断这个队列是否 满或空，以及得到当前队首和队尾的数据，共6个方法。

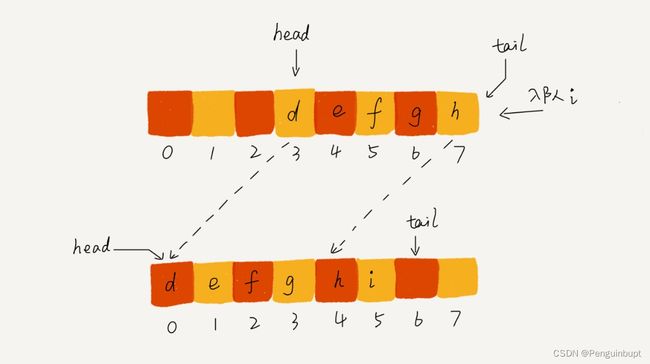
当我们在顺序队列中依次进行时，会出现 队首快到了最大索引，和队尾到了 数组的最大索引位置，此时出现入队操作，无法进行入队，前面的空闲位置又无法利用。

有一个方法是 将 front到rear指向的数据，进行移位，然后再进行入队操作。  这种方式需要移动数据，性能较差且耗时较长， 也就是说需要 “数据搬移”，这个操作时间复杂度为 O(n).

 于是 出现了循环队列，它解决了数据搬移的问题，使整个操作的时间降低，这就是“循环队列”

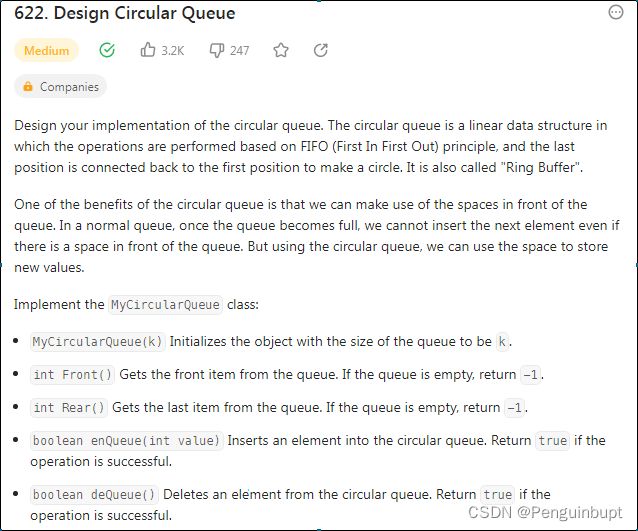
那我们如何实现一个循环队列呢？ 这也是LeetCode 第622题，如下图所示：

题解一： 使用 count 来记录 当前队列的元素个数来判断是否满或空

front指向队首，rear指向队尾应插入的位置， 这个队列的大小为k，申请空间也是k，所以它的占用率达到了100%，  我们无法让rear指向队尾，只能指向应当插入的地方，为什么呢 ?  

假设这个 当初始状态为 front = 1  rear = 0 时候，这种对于 队列size = 1时无法通过案例，因为这个方式最小的队列是1，所以无法使 front=1，rear=0.

初始状态： front = 0     rear = 0      //  "空的状态"

加入一个： front = 0     rear = 1      //  此后加入多个

临界状态： front = 0     rear = k-1   //  此时 索引 k-1 位置，这时候还有一个位置可用

再加一个： front = 0     rear = 0      //  此时是真的满了

“初始状态”和 “再加一个” 的状态 是相同的索引，我们无法区分是满还是空，所以我们引入 count值来认定当前队列是空还是满。

认为 初始状态，也就是空的状态，即 count == 0 ，每次入队就count++，每次出队就 count -- ，这种整体的利用率为 k/（k），利用率为100%，我们用C语言实现一下，以下代码通过了LeetCode，请放心食用。

typedef struct {
    int front;
    int rear;
    int size;
    int *arr;
    int count;    
} MyCircularQueue;
bool myCircularQueueIsEmpty(MyCircularQueue* obj);
bool myCircularQueueIsFull(MyCircularQueue* obj);
MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* p = malloc(sizeof(MyCircularQueue));
    p->size = k ;
    p->arr = malloc(sizeof(int)*(k));
    p->front = 0;
    p->rear = 0;
    p->count = 0;
    return p;
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
  if (myCircularQueueIsFull(obj)){
      return false;
  }else {
      obj->count++;
      *(obj->arr + obj->rear) = value;
      obj->rear = (obj->rear + 1)%(obj->size);
      return true;
  }
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
  if (myCircularQueueIsEmpty(obj)){
      return false;
  }else {
      obj->front = (obj->front + 1)%(obj->size);
      obj->count--;
      return true;
  }
}

int myCircularQueueFront(MyCircularQueue* obj) {
  if (myCircularQueueIsEmpty(obj)){
      return -1;
  }else {
      return *(obj->arr + obj->front);
  }
}

int myCircularQueueRear(MyCircularQueue* obj) {
  if (myCircularQueueIsEmpty(obj)){
      return -1;
  }else {
      int temp = (obj->rear - 1 + obj->size) % (obj->size);
      return *(obj->arr + temp);
  }
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    if ( obj->count == 0 ){
        return true;
    }else{
        return false;
    }
  
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    if ( obj->count == obj->size ){
        return true;
    }else{
        return false;
    }
}

void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->arr);
    free(obj);
}

题解二：front指向队首，rear指向队尾应插入的位置

初始状态： front = 0     rear = 0      //  "空的状态"

加入一个： front = 0     rear = 1      //  此后加入多个

临界状态： front = 0     rear =  k     //  此时 索引 k 位置，这时候还有一个位置可用

再加一个： front = 0     rear = 0      //  此时是真的满了，这种情况与 初始状态一样，所以无法区分满和空。

所以我们退而求其次，使用 “临界状态” 认为 “满的状态”， 即  (rear+1)%(k+1) == front

认为 初始状态，也就是空的状态，即 rear == front ，这种整体的利用率为 k/（k+1），当k趋于无穷大时候，利用率为100%，我们用C语言实现一下，以下代码通过了LeetCode，请放心食用。

typedef struct {
    int front;
    int rear;
    int size;
    int *arr;    
} MyCircularQueue;
bool myCircularQueueIsEmpty(MyCircularQueue* obj);
bool myCircularQueueIsFull(MyCircularQueue* obj);
MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* p = malloc(sizeof(MyCircularQueue));
    p->size = k + 1;
    p->arr = malloc(sizeof(int)*(k+1));
    p->front = 0;
    p->rear = 0;
    return p;
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
  if (myCircularQueueIsFull(obj)){
      return false;
  }else {
      *(obj->arr + obj->rear) = value;
      obj->rear = (obj->rear + 1)%(obj->size);
      return true;
  }
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
  if (myCircularQueueIsEmpty(obj)){
      return false;
  }else {
      obj->front = (obj->front + 1)%(obj->size);
      return true;
  }
}

int myCircularQueueFront(MyCircularQueue* obj) {
  if (myCircularQueueIsEmpty(obj)){
      return -1;
  }else {
      return *(obj->arr + obj->front);
  }
}

int myCircularQueueRear(MyCircularQueue* obj) {
  if (myCircularQueueIsEmpty(obj)){
      return -1;
  }else {
      int temp = obj->rear -1 ;
      if (temp < 0)temp = temp + obj->size;
      return *(obj->arr + temp);
  }
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    if ( obj->rear == obj->front ){
        return true;
    }else{
        return false;
    }
  
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    if ( (obj->rear + 1)%(obj->size) == obj->front ){
        return true;
    }else{
        return false;
    }
}

void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->arr);
    free(obj);
}

题解三： front指向队首，rear指向队尾

初始状态： front = 1     rear = 0      //  "空的状态"

加入一个： front = 1     rear = 1      //  此后加入多个

临界状态： front = 1     rear = k      //  索引 0位置，这时候还有一个位置可用

再加一个： front = 1     rear = 0      //  此时是真的满了，这种情况与 初始状态一样，所以无法区分满和空。

所以我们退而求其次，使用 “临界状态” 认为 “满的状态”， 即  (rear+2)%(k+1) == front

认为 初始状态，也就是空的状态，即 (rear+1)%(k+1) == front ，这种整体的利用率为 k/（k+1），当k趋于无穷大时候，利用率为100%，我们用C语言实现一下，以下代码通过了LeetCode，请放心食用。

typedef struct {
    int front;
    int rear;
    int size;
    int *arr;    
} MyCircularQueue;
bool myCircularQueueIsEmpty(MyCircularQueue* obj);
bool myCircularQueueIsFull(MyCircularQueue* obj);
MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* p = malloc(sizeof(MyCircularQueue));
    p->size = k + 1;
    p->arr = malloc(sizeof(int)*(k+1));
    p->front = 1;
    p->rear = 0;
    return p;
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
  if (myCircularQueueIsFull(obj)){
      return false;
  }else {
      obj->rear = (obj->rear + 1)%(obj->size);
      *(obj->arr + obj->rear) = value;
      return true;
  }
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
  if (myCircularQueueIsEmpty(obj)){
      return false;
  }else {
      obj->front = (obj->front + 1)%(obj->size);
      return true;
  }
}

int myCircularQueueFront(MyCircularQueue* obj) {
  if (myCircularQueueIsEmpty(obj)){
      return -1;
  }else {
      return *(obj->arr + obj->front);
  }
}

int myCircularQueueRear(MyCircularQueue* obj) {
  if (myCircularQueueIsEmpty(obj)){
      return -1;
  }else {
      return *(obj->arr + obj->rear);
  }
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    if ( (obj->rear + 1)%(obj->size) == obj->front ){
        return true;
    }else{
        return false;
    }
  
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    if ( (obj->rear + 2)%(obj->size) == obj->front ){
        return true;
    }else{
        return false;
    }
}

void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->arr);
    free(obj);
}

总结及注意事项：

1.  这题本质上是有两个不同的解决方法，其中一个是 保存个数来计算空和满，另一个是 按照公式来计算空和满。 题解二和题解三，只是rear指向不一样，这样他们的代码也会不一样。

其实 我推荐 题解三，无需引入count，且 front和rear均指向首尾元素，只是多利用了一个空间而已，k/(k+1) 约等于 100%， 缺点是需要记住公式，可以逆推。

如果front和rear均指向首尾元素，如果当队列只有一个元素，那么 front == rear，如果此时出队这个元素，front++，出现  front > rear 且 front -1 = rear，此时 队列为空。

我们假设 rear = 0 ，那么 front =1 来代表 空队列，即 (rear +1)%( obj->size) == front

此时我新增 k 个元素，得到 rear = k， 再增加一个元素，得到 rear = 0，此时无法与空队列进行区分，所以

满队列则为 rear = k  , front = 1  来代表 满队列,   即 ( rear + 2) % (obj->size ) == front

2. 如果用C语言来写，一定注意要先声明 满和空的函数，否则无法在其他函数里面使用。

bool myCircularQueueIsEmpty(MyCircularQueue* obj);
bool myCircularQueueIsFull(MyCircularQueue* obj);