手搓GPT系列之 - 通过理解LSTM的反向传播过程,理解LSTM解决梯度消失的原理 - 逐条解释LSTM创始论文全部推导公式,配超多图帮助理解(上篇)
1. 前言
说起RNN和LSTM,就绕不过Sepp Hochreiter 1997年的开山大作 Long Short-term Memory。奈何这篇文章写的实在是太劝退,整篇论文就2张图,网上很多介绍LSTM的文章都对这个模型反向传播的部分避重就轻,更少见(反正我没找到)有人解析APPENDIX A.1和A.2所写的详细推导过程。笔者向来做事讲究个从心,这次不知道哪根弦打错竟然头铁硬刚这个推导过程。本文逐条参照原论文中的公式,记录整个推导过程的思路和笔者的理解,学习神经网络的同学如果不满足于仅知道LSTM里各个门的功能,本文可以帮助大家理解了这个推导过程,进而能顺利理解为什么那几个门的设置可以解决RNN里的梯度消失和梯度爆炸的问题。好了,Dig in!
2. LSTM模型
2.1 原文中的示意图
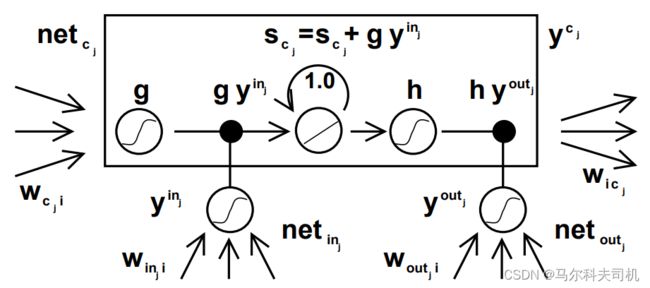
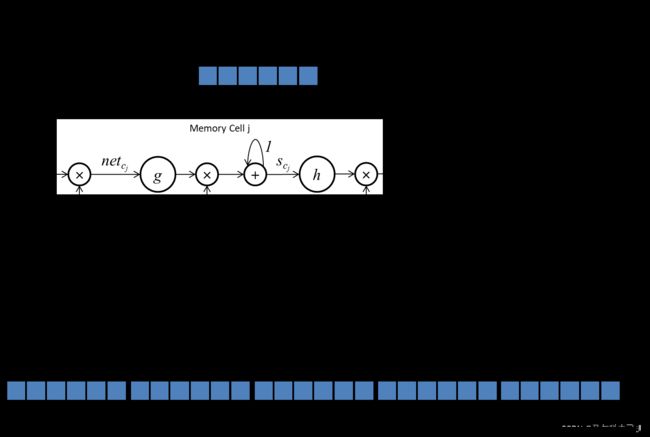
先给大家看最原汁原味的模型(LSTM论文中的图):
2.2 便于理解的示意图
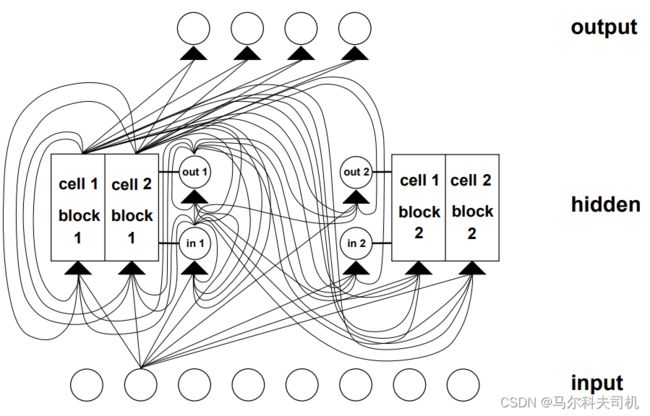
上边这两个图,第一张图还好,第二张图笔者一开始是看得一头雾水,第一张图有些关键信息也没有表现出来,不看也罢,所以笔者特地画了一张全景体现论文中所涉及到的所有节点的网络示意图。
上图展示了一个包含一个记忆单元(在一些文章中称为记忆细胞) c j c_j cj的LSTM网络。图中蓝色小方格 代表输入单元、输出单元或者用于存储中间状态的存储单元。包括输出单元 y k y^k yk,输入单元 x x x,输入门 y i n j y^{in_j} yinj,输出门 y o u t j y^{out_j} youtj,记忆单元激活状态 y c j y^{c_j} ycj,及隐藏单元的激活状态 y i y^i yi。输入门、输出门、记忆单元、隐藏单元激活等模块的输入 y u y^u yu包括输入单元、输入门激活、输出门激活、记忆单元激活等信息,输出单元的输入 y u : u n o t a g a t e y^{u:u\ not\ a\ gate} yu:u not a gate,包括记忆单元激活和隐藏单元激活两项,不包括输入输出门的激活和输入单元。接下来我们逐个分析LSTM文章中,APPENDIX A.1中的公式。
代表输入单元、输出单元或者用于存储中间状态的存储单元。包括输出单元 y k y^k yk,输入单元 x x x,输入门 y i n j y^{in_j} yinj,输出门 y o u t j y^{out_j} youtj,记忆单元激活状态 y c j y^{c_j} ycj,及隐藏单元的激活状态 y i y^i yi。输入门、输出门、记忆单元、隐藏单元激活等模块的输入 y u y^u yu包括输入单元、输入门激活、输出门激活、记忆单元激活等信息,输出单元的输入 y u : u n o t a g a t e y^{u:u\ not\ a\ gate} yu:u not a gate,包括记忆单元激活和隐藏单元激活两项,不包括输入输出门的激活和输入单元。接下来我们逐个分析LSTM文章中,APPENDIX A.1中的公式。
3. 前向过程
APPENDIX A.1的公式从(3)开始,所以我们也从(3)开始,以便于跟原文对应:
3.1 激活函数
总图中涉及到3中激活函数,分别为 f , g , h f,g,h f,g,h,其中 f f f是输入输出门,以及隐藏节点的激活函数,是一个sigmoid函数:
f ( x ) = 1 1 + e x p ( − x ) (3) f(x) = \frac{1}{1 + exp(-x)} \tag{3} f(x)=1+exp(−x)1(3)
h h h函数用于激活记忆单元的输出信息,是tanh函数:
h ( x ) = 2 1 + e x p ( − x ) − 1 (4) h(x) = \frac{2}{1 + exp(-x)} -1\tag{4} h(x)=1+exp(−x)2−1(4)
g g g函数用于激活记忆单元的输入信息:
g ( x ) = 4 1 + e x p ( − x ) − 2 (5) g(x) = \frac{4}{1 + exp(-x)} -2\tag{5} g(x)=1+exp(−x)4−2(5)
3.2 隐藏节点激活状态的计算
隐藏单元 i i i的激活函数计算公式:
n e t i ( t ) = ∑ u w i u y u ( t − 1 ) y i ( t ) = f i ( n e t i ( t ) ) . (6) \begin{aligned} net_i(t) &= \sum_u w_{iu}y_u(t-1) \\ y^i(t) &= f_i(net_i(t)). \end{aligned} \tag{6} neti(t)yi(t)=u∑wiuyu(t−1)=fi(neti(t)).(6)
这个公式对应了总图中的这个部分:
其中 y u y_u yu包含了输入单元 x x x,输入门激活状态 y i n j y^{in_j} yinj,输出门激活状态 y o u t j y^{out_j} youtj,记忆单元激活状态 y c j y^{c_j} ycj,以及隐藏单元本身的输出 y i y^i yi。隐藏单元激活状态的输出会更新 y i y^i yi,成为下一个时间步的输入的一部分。
3.3 输入门激活状态的计算
n e t i n j ( t ) = ∑ u w i n j u y u ( t − 1 ) y i n j ( t ) = f i n j ( n e t i n j ( t ) ) . (7) \begin{aligned} net_{in_j}(t) &= \sum_u w_{{in_j}u}y_u(t-1) \\ y^{in_j}(t) &= f_{in_j}(net_{in_j}(t)). \end{aligned} \tag{7} netinj(t)yinj(t)=u∑winjuyu(t−1)=finj(netinj(t)).(7)
对应于总图这一部分:
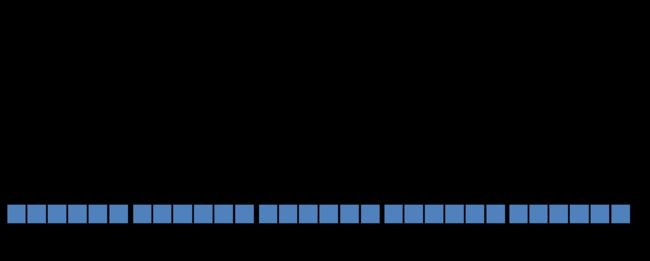
其中输入 y u y^u yu所包含的内容与隐藏节点激活状态计算过程中的 y u y^u yu一致,输出用于更新 y i n j y^{in_j} yinj。作为记忆单元的输入,另外,也作为整个网络下一个时间步输入的一部分。
3.4 输出门激活状态的计算
n e t o u t j ( t ) = ∑ u w o u t j u y u ( t − 1 ) y o u t j ( t ) = f o u t j ( n e t o u t j ( t ) ) . (8) \begin{aligned} net_{out_j}(t) &= \sum_u w_{{out_j}u}y_u(t-1) \\ y^{out_j}(t) &= f_{out_j}(net_{out_j}(t)). \end{aligned} \tag{8} netoutj(t)youtj(t)=u∑woutjuyu(t−1)=foutj(netoutj(t)).(8)
对应于总图这一部分:
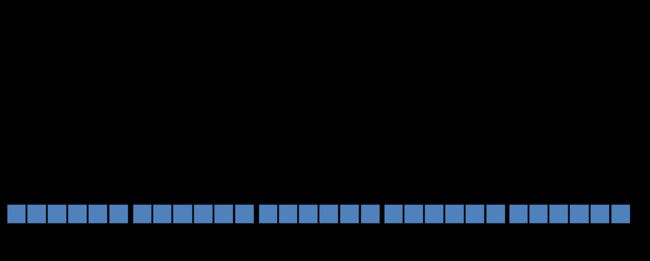
其中输入 y u y^u yu所包含的内容与隐藏节点激活状态计算过程中的 y u y^u yu一致,输出用于更新 y o u t j y^{out_j} youtj。作为记忆单元的输入,另外,也作为整个网络下一个时间步输入的一部分。
3.5 记忆单元的激活状态的计算
n e t c j ( t ) = ∑ u w c j u y u ( t − 1 ) s c j ( t ) = s c j ( t − 1 ) + y i n j ( t ) g ( n e t c j ( t ) ) y c j ( t ) = y o u t j ( t ) h ( s c j ( t ) ) . (9) \begin{aligned} net_{c_j}(t) &= \sum_u w_{{c_j}u}y_u(t-1) \\ s_{c_j}(t) &= s_{c_j}(t-1) + y^{in_j} (t) g(net_{c_j}(t)) \\ y^{c_j}(t) &=y^{out_j}(t) h(s_{c_j}(t)). \end{aligned} \tag{9} netcj(t)scj(t)ycj(t)=u∑wcjuyu(t−1)=scj(t−1)+yinj(t)g(netcj(t))=youtj(t)h(scj(t)).(9)
对应于总图的这一部分计算:
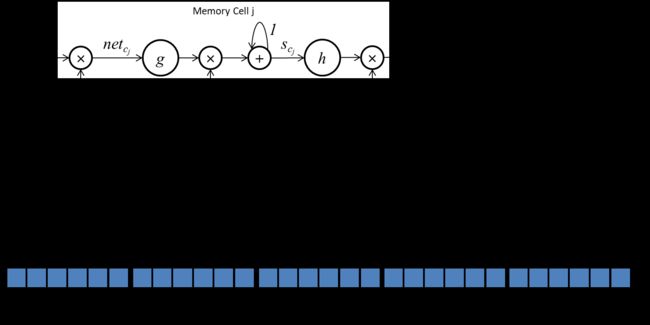
其中输入 y u y^u yu所包含的内容与隐藏节点激活状态计算过程中的 y u y^u yu一致,输出用于更新 y c j y^{c_j} ycj。作为整个网络下一个时间步输入的一部分。
3.6 输出单元激活状态的计算
n e t k ( t ) = ∑ u : u n o t a g a t e w k u y u ( t − 1 ) y k ( t ) = f k ( n e t k ( t ) ) . (8) \begin{aligned} net_{k}(t) &= \sum_{u:\ u\ not\ a\ gate} w_{{k}u}y_u(t-1) \\ y^{k}(t) &= f_{k}(net_{k}(t)). \end{aligned} \tag{8} netk(t)yk(t)=u: u not a gate∑wkuyu(t−1)=fk(netk(t)).(8)
对应于总图这一部分:
其中输入 y u y^u yu所包含的内容仅为 y c j , y i y^{c_j},y^i ycj,yi,输出作为网络输出。
4. 截断反向传播近似求导(Approximate derivatives for truncated backprop)
在本文中通过这个技术来简化反向传播过程。直觉上来说,就是将流入门或者记忆单元的误差信息截断在门或者记忆单元之内,确保门或者记忆单元的误差信息不会继续往外流动。由此确保了恒定误差转盘(CEC, Constant Error Carrousel)的实现。LSTM一文中,通过 ≈ t r \approx_{tr} ≈tr来表示被截断之后的近似导数。
4.1 截断求导的应用范围
应用截断后向传播之后,以下的求导公式的值会被设置为0:
∂ n e t i n j ( t ) ∂ y u ( t − 1 ) ≈ t r 0 ∀ u , ∂ n e t o u t j ( t ) ∂ y u ( t − 1 ) ≈ t r 0 ∀ u , ∂ n e t c j ( t ) ∂ y u ( t − 1 ) ≈ t r 0 ∀ u . \begin{aligned} \frac{\partial net _{in_j}(t)}{\partial y^u(t-1)} \approx_{tr} 0\ \forall{u},\\\\ \frac{\partial net _{out_j}(t)}{\partial y^u(t-1)} \approx_{tr} 0\ \forall{u},\\\\ \frac{\partial net _{c_j}(t)}{\partial y^u(t-1)} \approx_{tr} 0\ \forall{u}.\\ \end{aligned} ∂yu(t−1)∂netinj(t)≈tr0 ∀u,∂yu(t−1)∂netoutj(t)≈tr0 ∀u,∂yu(t−1)∂netcj(t)≈tr0 ∀u.
我们举输入门为例子,解释上边这三个式子的含义:

当错误信号通过 y i n j y^{in_j} yinj传进输入门时,假设流到 n e t i n j net_{in_j} netinj这里的错误信号为 v v v,此时输出到 y u y^u yu的错误信号会被截断为0。同样的情况也适用于其他门和记忆单元。
因此可以推导出:
∂ y i n j ( t ) ∂ y u ( t − 1 ) = f i n j ′ ( n e t i n j ( t ) ) ∂ n e t i n j ( t ) ∂ y u ( t − 1 ) ≈ t r 0 ∀ u , ∂ y o u t j ( t ) ∂ y u ( t − 1 ) = f o u t j ′ ( n e t o u t j ( t ) ) ∂ n e t o u t j ( t ) ∂ y u ( t − 1 ) ≈ t r 0 ∀ u . \begin{aligned} \frac{\partial y^{in_j}(t)}{\partial y^u(t-1)} = f'_{in_j}(net_{in_j}(t))\frac{\partial net_{in_j}(t)}{\partial y^u(t-1)} \approx_{tr}0\ \forall u,\\\\ \frac{\partial y^{out_j}(t)}{\partial y^u(t-1)} = f'_{out_j}(net_{out_j}(t))\frac{\partial net_{out_j}(t)}{\partial y^u(t-1)} \approx_{tr}0\ \forall u. \end{aligned} ∂yu(t−1)∂yinj(t)=finj′(netinj(t))∂yu(t−1)∂netinj(t)≈tr0 ∀u,∂yu(t−1)∂youtj(t)=foutj′(netoutj(t))∂yu(t−1)∂netoutj(t)≈tr0 ∀u.
以及:
∂ y c j ( t ) ∂ y u ( t − 1 ) = ∂ y c j ( t ) ∂ n e t o u t j ( t ) ∂ n e t o u t j ( t ) ∂ y u ( t − 1 ) + ∂ y c j ( t ) ∂ n e t i n j ( t ) ∂ n e t i n j ( t ) ∂ y u ( t − 1 ) + ∂ y c j ( t ) ∂ n e t c j ( t ) ∂ n e t c j ( t ) ∂ y u ( t − 1 ) ≈ t r 0 ∀ u . \frac{\partial y^{c_j}(t)}{\partial y^u(t-1)} = \frac{\partial y^{c_j}(t)}{\partial net_{out_j}(t)}\frac{\partial net_{out_j}(t)}{\partial y^u(t-1)} + \frac{\partial y^{c_j}(t)}{\partial net_{in_j}(t)}\frac{\partial net_{in_j}(t)}{\partial y^u(t-1)} + \frac{\partial y^{c_j}(t)}{\partial net_{c_j}(t)}\frac{\partial net_{c_j}(t)}{\partial y^u(t-1)}\approx_{tr}0\ \forall u. ∂yu(t−1)∂ycj(t)=∂netoutj(t)∂ycj(t)∂yu(t−1)∂netoutj(t)+∂netinj(t)∂ycj(t)∂yu(t−1)∂netinj(t)+∂netcj(t)∂ycj(t)∂yu(t−1)∂netcj(t)≈tr0 ∀u.
我们利用记忆单元举例说明上边这三个式子的直觉解释:
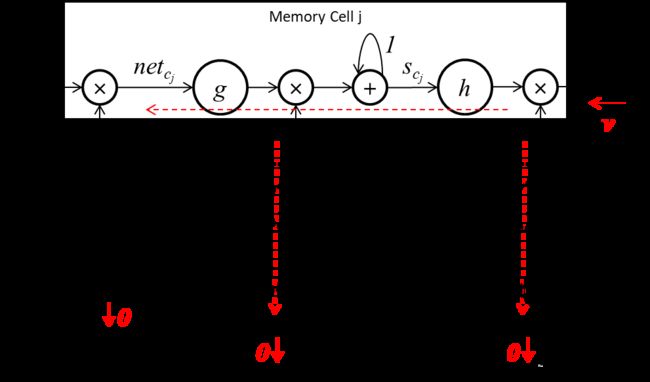
从记忆单元激活状态 y c j y^{c_j} ycj流入的误差信息,在记忆单元内部流转之后,经过 n e t c j net_{c_j} netcj流到 y u y^u yu处流出的误差信息被强制截断为0。同样误差信息经 y i n j y^{in_j} yinj流入输入门,再流到 y u y^u yu时,误差信息被截断为0。经 y o u t j y^{out_j} youtj流入输出门,再流到 y u y^u yu时,误差信息被截断为0。
综合上述公式,我们可以得到,对于任何 w l m w_{lm} wlm非直接与记忆单元及门( c j , i n j , o u t j c_{j},in_j,out_j cj,inj,outj)连接的,即( l ∉ { c j , i n j , o u t j } l \notin\{c_j, in_j, out_j\} l∈/{cj,inj,outj}):
∂ y c j ( t ) ∂ w l m = ∑ u ∂ y c j ( t ) ∂ y u ( t − 1 ) ∂ y u ( t − 1 ) ∂ w l m \frac{\partial y^{c_j}(t)}{\partial w_{lm}}= \sum_u \frac{\partial y^{c_j}(t)}{\partial y^u(t-1)} \frac{\partial y^u(t-1)}{\partial w_{lm}} ∂wlm∂ycj(t)=u∑∂yu(t−1)∂ycj(t)∂wlm∂yu(t−1)
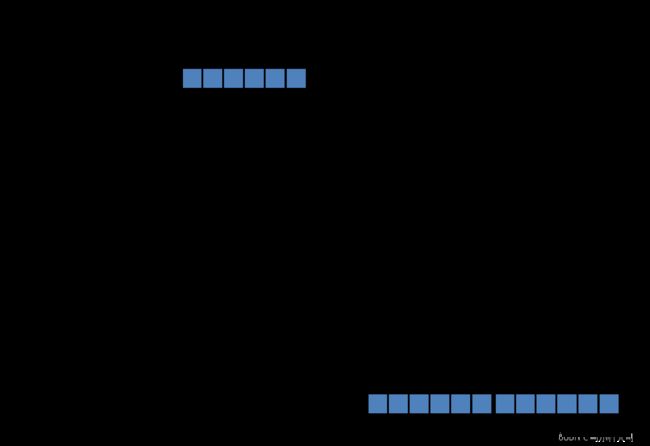
上边这个式子可以理解为,所有只能通过 y u y^u yu与记忆单元、输入输出门连接的网络,都不会收到从记忆单元激活状态输出处传来的错误信号。一般来说是谁与记忆单元和门通过 y u y^u yu间接连接的呢?有几种,第一种就是上一个时间步的记忆单元、输入输出门的激活状态,记为 y i n j ( t − 1 ) , y o u t j ( t − 1 ) , y c j ( t − 1 ) y^{in_j}(t-1),y^{out_j}(t-1),y^{c_j}(t-1) yinj(t−1),youtj(t−1),ycj(t−1);另一种就是隐藏单元激活状态。下边这张图可以帮助大家理解上边这个公式的含义:
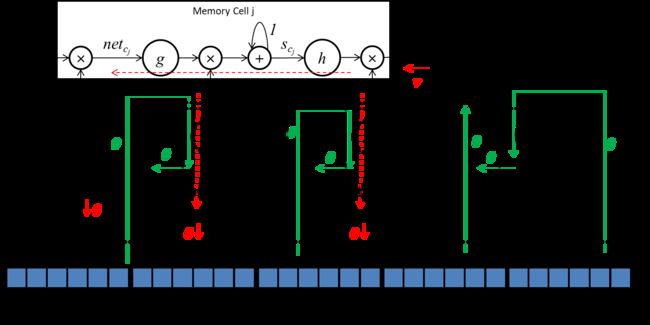
红色箭头和数字,表示 t t t时间步下,从 y c j y^{c_j} ycj传入的误差信息的传播路径,绿色箭头和数字,表示 t − 1 t-1 t−1时间步下的误差信息的传播路径。用一句话概括就是,误差信号被门和记忆单元隔开,不会随着时间步循环后向传播。
4.2 输出单元的截断求导
关于输出节点在t时刻的截断求导公式是:
∂ y k ( t ) w l m = f k ′ ( n e t k ( t − 1 ) ) ( ∑ u : u n o t a g a t e w k u ∂ y u ( t − 1 ) ∂ w l m + δ k l y m ( t − 1 ) ) ≈ t r f k ′ ( n e t k ( t ) ) { y m ( t − 1 ) l = k w k c j ∂ y c j ( t − 1 ) ∂ w l m l = c j w k c j ∂ y c j ( t − 1 ) ∂ w l m l = i n j o r l = o u t j ∑ i : i h i d d e n u n i t w k i ∂ y i ( t − 1 ) ∂ w l m o t h e r w i s e (10) \begin{aligned} \frac{\partial y^k(t)}{w_{lm}} = & f'_k(net_k(t-1))( \sum_{u:\ u\ not\ a\ gate} w_{ku} \frac{\partial y^u(t-1)}{\partial w_{lm}} + \delta_{kl}y^m(t-1))\\ \approx_{tr} & f'_k(net_k(t)) \begin{cases} y^m(t-1) & l=k \\ w_{kc_{j}}\frac{\partial y^{c_j}(t-1)}{\partial w_{lm}} & l=c_j\\ w_{kc_{j}}\frac{\partial y^{c_j}(t-1)}{\partial w_{lm}} & l=in_j\ or\ l=out_j\\ \sum_{i:\ i\ hidden\ unit} w_{ki} \frac{\partial y^i(t-1)}{\partial w_{lm}} & otherwise \end{cases} \end{aligned} \tag{10} wlm∂yk(t)=≈trfk′(netk(t−1))(u: u not a gate∑wku∂wlm∂yu(t−1)+δklym(t−1))fk′(netk(t))⎩ ⎨ ⎧ym(t−1)wkcj∂wlm∂ycj(t−1)wkcj∂wlm∂ycj(t−1)∑i: i hidden unitwki∂wlm∂yi(t−1)l=kl=cjl=inj or l=outjotherwise(10)
上述公式中, δ \delta δ表示克罗内克函数(kronecker delta),即 ( i = j ) ⇔ ( δ i j = 1 ) A N D ( i ≠ j ) ⇔ ( δ i j = 0 ) (i=j) \Leftrightarrow (\delta_{ij} = 1)\ AND\ (i\ne j) \Leftrightarrow (\delta_{ij} = 0) (i=j)⇔(δij=1) AND (i=j)⇔(δij=0)。我们来解读上边这个式子:
当 l = k l=k l=k时,我们有:
∂ y k ( t ) w l m = ∂ y k ( t ) w k m = f k ′ ( n e t k ( t ) ) ∂ ∑ u : u n o t a g a t e w k u y u ( t − 1 ) ∂ w k m = f k ′ ( n e t k ( t ) ) y m ( t − 1 ) \begin{aligned} \frac{\partial y^k(t)}{w_{lm}} &= \frac{\partial y^k(t)}{w_{km}}\\ &= f'_k(net_k(t)) \frac{\partial \sum_{u:\ u\ not\ a\ gate} w_{ku}y^u(t-1)}{\partial w_{km}}\\ & = f'_k(net_k(t)) y^m(t-1) \end{aligned} wlm∂yk(t)=wkm∂yk(t)=fk′(netk(t))∂wkm∂∑u: u not a gatewkuyu(t−1)=fk′(netk(t))ym(t−1)
下图显示了 l = k l=k l=k时 ∂ y k ( t ) w l m \frac{\partial y^k(t)}{w_{lm}} wlm∂yk(t)的误差传播路线(红色箭头):
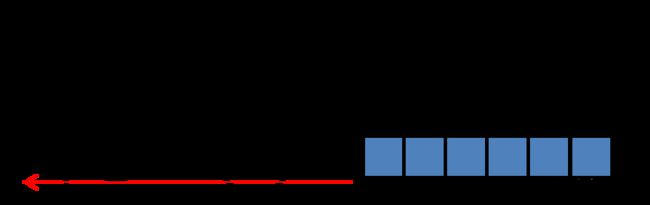
当 l = c j l=c_j l=cj时,也就是求 y k ( t ) y^k(t) yk(t)关于记忆单元输入(注意不是输入门)的网络的权重 w c j w_{c_j} wcj的偏导。原文是把 c j c_j cj写成 c j v c_j^v cjv,因为一个完整的LSTM网络可以包含 p p p( c ∈ [ 1 , . . . , p ] c \in [1,...,p] c∈[1,...,p])个记忆块(memory block),每个记忆块可以有 q q q( j ∈ [ 1 , . . . , q ] j \in [1,...,q] j∈[1,...,q])个记忆单元。因此 c j v c_j^v cjv表示第 v v v个记忆块中的第 j j j个记忆单元。为了方便理解,笔者把LSTM网络简化成一个单记忆块,单记忆单元的网络。标记则省略记忆块的标记,只保留记忆单元的标记,因此就简化成了 c j c_j cj,表示第 j j j个记忆单元。我们现在来理解一下输出单元激活值 y k y^k yk关于记忆单元的输入权重 w c j w_{c_j} wcj的偏导:
∂ y k ( t ) w l m = ∂ y k ( t ) w c j m = f k ′ ( n e t k ( t ) ) ∂ ∑ u : u n o t a g a t e w k u y u ( t − 1 ) ∂ w c j m = f k ′ ( n e t k ( t ) ) ∂ ∑ u : u n o t a g a t e w k u y u ( t − 1 ) ∂ y c j ( t − 1 ) ∂ y c j ( t − 1 ) ∂ w c j m = f k ′ ( n e t k ( t ) ) w k c j ∂ y c j ( t − 1 ) ∂ w c j m \begin{aligned} \frac{\partial y^k(t)}{w_{lm}} &= \frac{\partial y^k(t)}{w_{{c_j}m}}\\ &= f'_k(net_k(t)) \frac{\partial \sum_{u:\ u\ not\ a\ gate} w_{{k}u}y^u(t-1)}{\partial w_{{c_j}m}}\\ &= f'_k(net_k(t)) \frac{\partial \sum_{u:\ u\ not\ a\ gate} w_{{k}u}y^u(t-1)}{\partial y^{c_j}(t-1)} \frac{\partial y^{c_j}(t-1)}{\partial w_{{c_j}m}}\\ & = f'_k(net_k(t)) w_{k{c_j}} \frac{\partial y^{c_j}(t-1)}{\partial w_{{c_j}m}} \end{aligned} wlm∂yk(t)=wcjm∂yk(t)=fk′(netk(t))∂wcjm∂∑u: u not a gatewkuyu(t−1)=fk′(netk(t))∂ycj(t−1)∂∑u: u not a gatewkuyu(t−1)∂wcjm∂ycj(t−1)=fk′(netk(t))wkcj∂wcjm∂ycj(t−1)
误差传播路线:
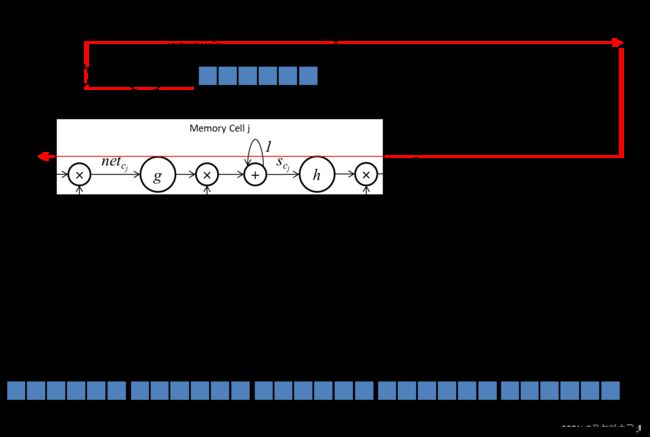
当 l = i n j l=in_j l=inj时,可以得到:
∂ y k ( t ) w l m = ∂ y k ( t ) w i n j m = f k ′ ( n e t k ( t ) ) ∂ ∑ u : u n o t a g a t e w k u y u ( t − 1 ) ∂ w i n j m = f k ′ ( n e t k ( t ) ) ∂ ∑ u : u n o t a g a t e w k u y u ( t − 1 ) ∂ y c j ( t − 1 ) ∂ y c j ( t − 1 ) ∂ w i n j m = f k ′ ( n e t k ( t ) ) w k c j ∂ y c j ( t − 1 ) ∂ w i n j m \begin{aligned} \frac{\partial y^k(t)}{w_{lm}} &= \frac{\partial y^k(t)}{w_{{in_j}m}}\\ &= f'_k(net_k(t)) \frac{\partial \sum_{u:\ u\ not\ a\ gate} w_{{k}u}y^u(t-1)}{\partial w_{{in_j}m}}\\ &= f'_k(net_k(t)) \frac{\partial \sum_{u:\ u\ not\ a\ gate} w_{{k}u}y^u(t-1)}{\partial y^{c_j}(t-1)} \frac{\partial y^{c_j}(t-1)}{\partial w_{{in_j}m}}\\ & = f'_k(net_k(t)) w_{k{c_j}} \frac{\partial y^{c_j}(t-1)}{\partial w_{{in_j}m}} \end{aligned} wlm∂yk(t)=winjm∂yk(t)=fk′(netk(t))∂winjm∂∑u: u not a gatewkuyu(t−1)=fk′(netk(t))∂ycj(t−1)∂∑u: u not a gatewkuyu(t−1)∂winjm∂ycj(t−1)=fk′(netk(t))wkcj∂winjm∂ycj(t−1)
误差传播路线:
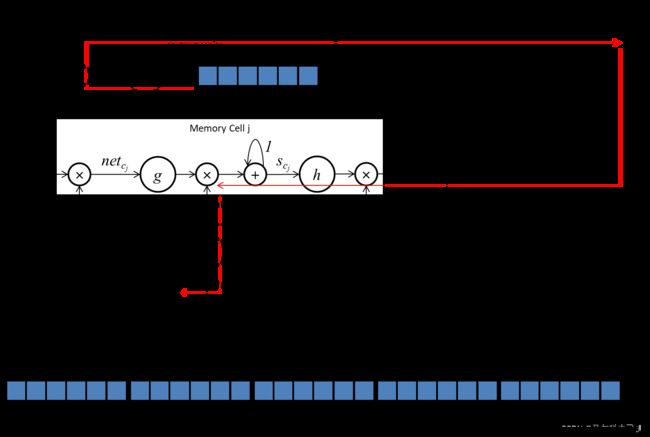
由于我们的例子中简化了记忆单元的结构,LSTM原文中,实际上是有多个记忆单元,并且多个记忆单元可以组成一个记忆单元块。每个记忆单元块可以直接连接其前面所有的记忆单元的输出,因此原文中,当 l = i n j l=in_j l=inj时,计算公式为:
∂ y k ( t ) w l m = ∑ v = 1 s j f k ′ ( n e t k ( t ) ) w k c j ∂ y c j v ( t − 1 ) ∂ w i n j m \begin{aligned} \frac{\partial y^k(t)}{w_{lm}} &= \sum_{v=1}^{s_j} f'_k(net_k(t)) w_{k{c_j}} \frac{\partial y^{c_j^v}(t-1)}{\partial w_{{in_j}m}} \end{aligned} wlm∂yk(t)=v=1∑sjfk′(netk(t))wkcj∂winjm∂ycjv(t−1)
其中 c j v c^v_j cjv表示第 v v v个记忆单元块中的第 j j j个记忆单元。
当 l = o u t j l=out_j l=outj时,通过与上面一样的及算法方法可以得到:
∂ y k ( t ) w l m = f k ′ ( n e t k ( t ) ) w k c j ∂ y c j ( t − 1 ) ∂ w o u t j m \begin{aligned} \frac{\partial y^k(t)}{w_{lm}} & = f'_k(net_k(t)) w_{k{c_j}} \frac{\partial y^{c_j}(t-1)}{\partial w_{{out_j}m}} \end{aligned} wlm∂yk(t)=fk′(netk(t))wkcj∂woutjm∂ycj(t−1)
误差传播路线:
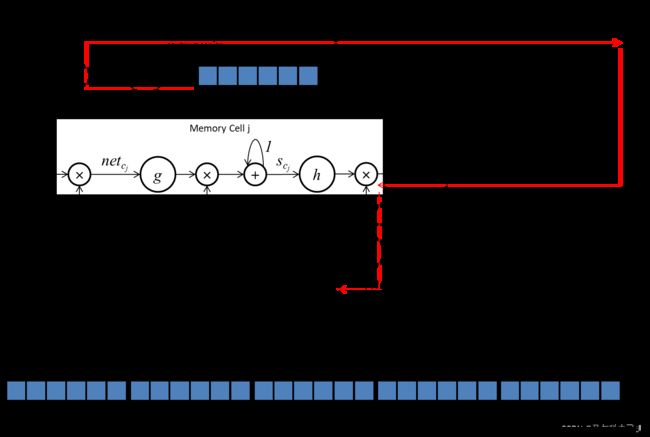
当 l = i l=i l=i,我们可以得到:
∂ y k ( t ) w l m = ∂ y k ( t ) w i m = f k ′ ( n e t k ( t ) ) ∂ ∑ i : i h i d d e n u n i t s w k u y u ( t − 1 ) ∂ w i m = f k ′ ( n e t k ( t ) ) ∂ ∑ i : i h i d d e n u n i t s w k u y u ( t − 1 ) ∂ y i ( t − 1 ) ∂ y i ( t − 1 ) ∂ w i m = f k ′ ( n e t k ( t ) ) w k i ∂ y i ( t − 1 ) ∂ w i m \begin{aligned} \frac{\partial y^k(t)}{w_{lm}} &= \frac{\partial y^k(t)}{w_{{i}m}}\\ &= f'_k(net_k(t)) \frac{\partial \sum_{i:\ i\ hidden\ units} w_{{k}u}y^u(t-1)}{\partial w_{{i}m}}\\ &= f'_k(net_k(t)) \frac{\partial \sum_{i:\ i\ hidden\ units} w_{{k}u}y^u(t-1)}{\partial y^{i}(t-1)} \frac{\partial y^{i}(t-1)}{\partial w_{{i}m}}\\ & = f'_k(net_k(t)) w_{k{i}} \frac{\partial y^{i}(t-1)}{\partial w_{{i}m}} \end{aligned} wlm∂yk(t)=wim∂yk(t)=fk′(netk(t))∂wim∂∑i: i hidden unitswkuyu(t−1)=fk′(netk(t))∂yi(t−1)∂∑i: i hidden unitswkuyu(t−1)∂wim∂yi(t−1)=fk′(netk(t))wki∂wim∂yi(t−1)
误差传播路线为:
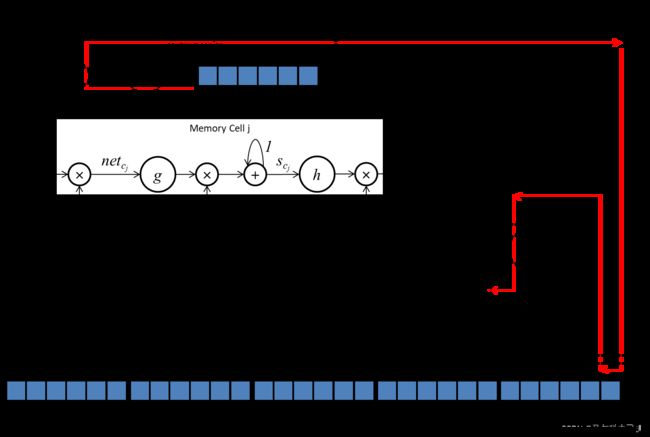
4.3 隐藏单元的截断求导
隐藏单元的求导公式如下:
∂ y i ∂ w l m = f i ′ ( n e t i ( t ) ) n e t i ( t ) ∂ w l m ≈ t r δ l i f i ′ ( n e t i ( t ) ) y m ( t − 1 ) . (11) \frac{\partial y^i}{\partial w_{lm}} = f'_i(net_i(t))\frac{net_i(t)}{\partial w_{lm}}\approx_{tr}\delta_{li}f'_i(net_i(t))y^m(t-1). \tag{11} ∂wlm∂yi=fi′(neti(t))∂wlmneti(t)≈trδlifi′(neti(t))ym(t−1).(11)
这个求导公式比较一目了然,感觉没什么好说的,我们放一个误差传播路径的示意图上来:
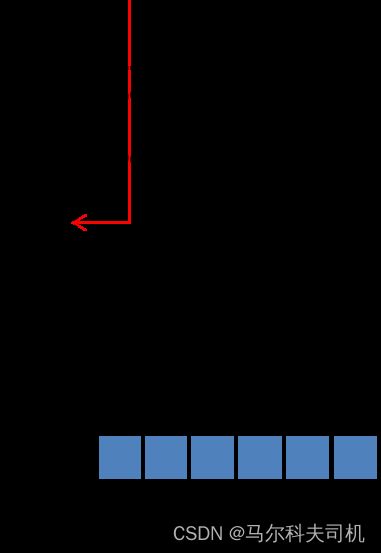
4.4 输入输出门及记忆单元的激活状态的截断求导
先看输入门的截断求导公式:
∂ y i n j ( t ) ∂ w l m = f i n j ′ ( n e t i n j ( t ) ) ∂ n e t i n j ( t ) ∂ w l m ≈ t r δ i n j l f i n j ′ ( n e t i n j ( t ) ) y m ( t − 1 ) (12) \begin{aligned} \frac{\partial y^{in_j}(t)}{\partial w_{lm}} =& f'_{in_j}(net_{in_j}(t))\frac{\partial net_{in_j}(t)}{\partial w_{lm}} \\ \approx_{tr} & \delta_{in_jl}f'_{in_j}(net_{in_j}(t))y^m(t-1) \end{aligned} \tag{12} ∂wlm∂yinj(t)=≈trfinj′(netinj(t))∂wlm∂netinj(t)δinjlfinj′(netinj(t))ym(t−1)(12)
这个公式的意思就是,当且仅当 l = i n j l=in_j l=inj时,该公式有非零的值。同样的道理也适用于输出门的求导:
∂ y o u t j ( t ) ∂ w l m = f o u t j ′ ( n e t o u t j ( t ) ) ∂ n e t o u t j ( t ) ∂ w l m ≈ t r δ o u t j l f o u t j ′ ( n e t o u t j ( t ) ) y m ( t − 1 ) (13) \begin{aligned} \frac{\partial y^{out_j}(t)}{\partial w_{lm}} =& f'_{out_j}(net_{out_j}(t))\frac{\partial net_{out_j}(t)}{\partial w_{lm}} \\ \approx_{tr} & \delta_{out_jl}f'_{out_j}(net_{out_j}(t))y^m(t-1) \end{aligned} \tag{13} ∂wlm∂youtj(t)=≈trfoutj′(netoutj(t))∂wlm∂netoutj(t)δoutjlfoutj′(netoutj(t))ym(t−1)(13)
接下来是 s c j s_{c_j} scj的求导公式:
∂ s c j ( t ) ∂ w l m = ∂ s c j ( t − 1 ) ∂ w l m + ∂ g ( n e t c j ( t ) ) f i n j ( n e t i n j ( t ) ) ∂ w l m = ∂ s c j ( t − 1 ) ∂ w l m + ∂ g ( n e t c j ( t ) ) ∂ w l m f i n j ( n e t i n j ( t ) ) + ∂ f i n j ( n e t i n j ( t ) ) ∂ w l m g ( n e t c j ( t ) ) = ∂ s c j ( t − 1 ) ∂ w l m + ∂ g ( n e t c j ( t ) ) ∂ w l m y i n j ( t ) + ∂ y i n j ( t ) ∂ w l m g ( n e t c j ( t ) ) = ∂ s c j ( t − 1 ) ∂ w l m + ∂ n e t c j ( t ) ∂ w l m g ′ ( n e t c j ( t ) ) y i n j ( t ) + ∂ y i n j ( t ) ∂ w l m g ( n e t c j ( t ) ) ≈ t r ( δ c j l + δ i n j l ) ∂ s c j ( t − 1 ) ∂ w l m + δ i n j l ∂ y i n j ( t ) ∂ w l m g ( n e t c j ( t ) ) + δ c j l y i n j ( t ) g ′ ( n e t c j ( t ) ) ∂ n e t c j ( t ) ∂ w l m = ( δ c j l + δ i n j l ) ∂ s c j ( t − 1 ) ∂ w l m + δ i n j l g ( n e t c j ( t ) ) f i n j ′ ( n e t i n j ( t ) ) y m ( t − 1 ) + δ c j l y i n j ( t ) g ′ ( n e t c j ( t ) ) y m ( t − 1 ) (14) \begin{aligned} \frac{\partial s_{c_j}(t)}{\partial w_{lm}}=&\frac{\partial s_{c_j}(t-1)}{\partial w_{lm}} + \frac{\partial g(net_{c_j}(t))f_{in_j}(net_{in_j}(t))}{\partial w_{lm}}\\ =& \frac{\partial s_{c_j}(t-1)}{\partial w_{lm}} + \frac{\partial g(net_{c_j}(t))}{\partial w_{lm}}f_{in_j}(net_{in_j}(t)) + \frac{\partial f_{in_j}(net_{in_j}(t))}{\partial w_{lm}}g(net_{c_j}(t))\\ =& \frac{\partial s_{c_j}(t-1)}{\partial w_{lm}} + \frac{\partial g(net_{c_j}(t))}{\partial w_{lm}}y^{in_j}(t) + \frac{\partial y^{in_j}(t)}{\partial w_{lm}}g(net_{c_j}(t))\\ =& \frac{\partial s_{c_j}(t-1)}{\partial w_{lm}} + \frac{\partial net_{c_j}(t)}{\partial w_{lm}}g'(net_{c_j}(t))y^{in_j}(t) + \frac{\partial y^{in_j}(t)}{\partial w_{lm}}g(net_{c_j}(t))\\ \approx_{tr}& (\delta_{{c_j}l} + \delta_{{in_j}l})\frac{\partial s_{c_j}(t-1)}{\partial w_{lm}} + \delta_{{in_j}l} \frac{\partial y^{in_j}(t)}{\partial w_{lm}}g(net_{c_j}(t)) + \delta_{{c_j}l}y^{in_j}(t)g'(net_{c_j}(t))\frac{\partial net_{c_j}(t)}{\partial w_{lm}}\\ =& (\delta_{{c_j}l} + \delta_{{in_j}l})\frac{\partial s_{c_j}(t-1)}{\partial w_{lm}} + \delta_{{in_j}l}g(net_{c_j}(t)) f'_{in_j}(net_{in_j}(t))y^m(t-1) + \delta_{{c_j}l}y^{in_j}(t)g'(net_{c_j}(t))y^{m}(t-1) \end{aligned} \tag{14} ∂wlm∂scj(t)====≈tr=∂wlm∂scj(t−1)+∂wlm∂g(netcj(t))finj(netinj(t))∂wlm∂scj(t−1)+∂wlm∂g(netcj(t))finj(netinj(t))+∂wlm∂finj(netinj(t))g(netcj(t))∂wlm∂scj(t−1)+∂wlm∂g(netcj(t))yinj(t)+∂wlm∂yinj(t)g(netcj(t))∂wlm∂scj(t−1)+∂wlm∂netcj(t)g′(netcj(t))yinj(t)+∂wlm∂yinj(t)g(netcj(t))(δcjl+δinjl)∂wlm∂scj(t−1)+δinjl∂wlm∂yinj(t)g(netcj(t))+δcjlyinj(t)g′(netcj(t))∂wlm∂netcj(t)(δcjl+δinjl)∂wlm∂scj(t−1)+δinjlg(netcj(t))finj′(netinj(t))ym(t−1)+δcjlyinj(t)g′(netcj(t))ym(t−1)(14)
最后就是记忆单元的激活状态求导:
∂ y c j ( t ) ∂ w l m = ∂ y o u t j ( t ) ∂ w l m h ( s c j ( t ) ) + ∂ h ( s c j ( t ) ) ∂ w l m y o u t j ( t ) = ∂ y o u t j ( t ) ∂ w l m h ( s c j ( t ) ) + h ′ ( s c j ( t ) ) ∂ s c j ( y ) ∂ w l m y o u t j ( t ) = f o u t j ′ ( n e t o u t j ( t ) ) y m ( t − 1 ) h ( s c j ( t ) ) + h ′ ( s c j ( t ) ) ∂ s c j ( y ) ∂ w l m y o u t j ( t ) ≈ t r δ o u t j l f o u t j ′ ( n e t o u t j ( t ) ) y m ( t − 1 ) h ( s c j ( t ) ) + ( δ c j l + δ i n j l ) h ′ ( s c j ( t ) ) ∂ s c j ( y ) ∂ w l m y o u t j ( t ) (15) \begin{aligned} \frac{\partial y^{c_j}(t)}{\partial w_{lm}} =& \frac{\partial y^{out_j}(t)}{\partial w_{lm}} h(s_{c_j}(t)) + \frac{\partial h(s_{c_j}(t))}{\partial w_{lm}} y^{out_j}(t)\\ =& \frac{\partial y^{out_j}(t)}{\partial w_{lm}} h(s_{c_j}(t)) + h'(s_{c_j}(t))\frac{\partial s_{c_j}(y)}{\partial w_{lm}}y^{out_j}(t)\\ =& f'_{out_j}(net_{out_j}(t))y^m(t-1) h(s_{c_j}(t)) + h'(s_{c_j}(t))\frac{\partial s_{c_j}(y)}{\partial w_{lm}}y^{out_j}(t)\\ \approx_{tr}& \delta_{out_jl}f'_{out_j}(net_{out_j}(t))y^m(t-1) h(s_{c_j}(t)) + (\delta_{{c_j}l} + \delta_{{in_j}l})h'(s_{c_j}(t))\frac{\partial s_{c_j}(y)}{\partial w_{lm}}y^{out_j}(t)\\ \end{aligned} \tag{15} ∂wlm∂ycj(t)===≈tr∂wlm∂youtj(t)h(scj(t))+∂wlm∂h(scj(t))youtj(t)∂wlm∂youtj(t)h(scj(t))+h′(scj(t))∂wlm∂scj(y)youtj(t)foutj′(netoutj(t))ym(t−1)h(scj(t))+h′(scj(t))∂wlm∂scj(y)youtj(t)δoutjlfoutj′(netoutj(t))ym(t−1)h(scj(t))+(δcjl+δinjl)h′(scj(t))∂wlm∂scj(y)youtj(t)(15)
根据公式(14),(15)可知,若要计算记忆单元 j j j在 t t t时间步下的激活状态 y c j ( t ) y^{c_j}(t) ycj(t)关于 w l m w_{lm} wlm的本地误差因子,需要计算如下的参数: ∂ s c j ( t − 1 ) ∂ w l m \frac{\partial s_{c_j}(t-1)}{\partial w_{lm}} ∂wlm∂scj(t−1), g ( n e t c j ( t ) ) g(net_{c_j}(t)) g(netcj(t)), f i n j ′ ( n e t i n j ( t ) ) f'_{in_j}(net_{in_j}(t)) finj′(netinj(t)), y m ( t − 1 ) y^m(t-1) ym(t−1), y i n j ( t ) y^{in_j}(t) yinj(t), g ′ ( n e t c j ( t ) ) g'(net_{c_j}(t)) g′(netcj(t)), f o u t j ′ ( n e t o u t j ( t ) ) f'_{out_j}(net_{out_j}(t)) foutj′(netoutj(t)), h ( s c j ( t ) ) h(s_{c_j}(t)) h(scj(t)), h ′ ( s c j ( t ) ) h'(s_{c_j}(t)) h′(scj(t)), y o u t j ( t ) y^{out_j}(t) youtj(t)。
| 参数 | 条件 | 获取方法 |
|---|---|---|
| ∂ s c j ( t − 1 ) ∂ w l m \frac{\partial s_{c_j}(t-1)}{\partial w_{lm}} ∂wlm∂scj(t−1) | l = i n j o r l = c j l=in_{j}\ or\ l=c_j l=inj or l=cj | 正向传播过程中计算并保存 |
| g ( n e t c j ( t ) ) g(net_{c_j}(t)) g(netcj(t)) | l = i n j l=in_{j} l=inj | 实时计算 |
| f i n j ′ ( n e t i n j ( t ) ) f'_{in_j}(net_{in_j}(t)) finj′(netinj(t)) | l = i n j l=in_{j} l=inj | 实时计算 |
| y m ( t − 1 ) y^m(t-1) ym(t−1) | l = i n j o r l = c j o r l = o u t j l=in_{j}\ or\ l=c_j\ or\ l=out_j l=inj or l=cj or l=outj | 正向传播过程中计算并保存 |
| y i n j ( t ) y^{in_j}(t) yinj(t) | l = c j l=c_j l=cj | 实时计算 |
| g ′ ( n e t c j ( t ) ) g'(net_{c_j}(t)) g′(netcj(t)) | l = c j l=c_j l=cj | 实时计算 |
| f o u t j ′ ( n e t o u t j ( t ) ) f'_{out_j}(net_{out_j}(t)) foutj′(netoutj(t)) | l = o u t j l=out_j l=outj | 实时计算 |
| h ( s c j ( t ) ) h(s_{c_j}(t)) h(scj(t)) | l = o u t j l=out_j l=outj | 实时计算 |
| h ′ ( s c j ( t ) ) h'(s_{c_j}(t)) h′(scj(t)) | l = i n j o r l = c j l=in_{j}\ or\ l=c_j l=inj or l=cj | 实时计算 |
| y o u t j ( t ) y^{out_j}(t) youtj(t) | l = i n j o r l = c j l=in_{j}\ or\ l=c_j l=inj or l=cj | 实时计算 |
需要在正向传播过程中保存偏导数的情况为:当 l = i n j o r l = c j l=in_{j}\ or\ l=c_j l=inj or l=cj时,保存 ∂ s c j ( t − 1 ) ∂ w l m \frac{\partial s_{c_j}(t-1)}{\partial w_{lm}} ∂wlm∂scj(t−1)。 y m ( t ) y^{m}(t) ym(t)值也需要在前向传播过程中计算并保存,后向过程中的其他参数都可以在传播过程中实时生成。
由于文章太长,我们将把整个文章分为上下两篇,上篇介绍正向传播过程的公式以及各个计算单元的截断求导公式的详细解读。下篇我将给大家介绍后向传播过程的详细解读。