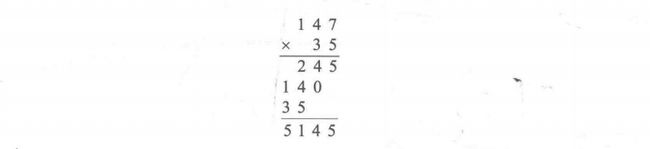大整数的四则运算(高精度计算)(c语言)
大整数运算
对于一道A + B的题目,如果A 和B的范围在int范围内,那么相信大家很快就能写出程序,但如果A和B是有着1000个数位的整数,那就已经没有数据类型来表示了,这时就只能老老实实去模拟加减乘除的过程,实际上这些东西的原理都是小学的知识。此外大整数又称为高精度整数,其含义就是用基本数据类型无法存储其精度的整数。
1.大整数的存储
用一个数组来存放整数的每一位,并将整数的高位存储在数组的高位,整数的低位存储在数组的低位,为了方便随时获取大整数的长度,一般都会定义一个int变量类型的len记录其长度,并和数组组成结构体 如下:
//大整数结构体
struct bign {
int d[1000];
int len;
bign() { //初始化结构体
memset(d, 0, sizeof(d));
len = 0;
}
};
2.大整数的输入
//输入大整数
bign change(char str[]) { //将整数转换为bign
bign a;
a.len = strlen(str);
for (int i = 0; i < a.len; i++) {
a.d[i] = str[a.len - 1 - i] - '0';//逆序赋值
}
return a;
}3.比较两个大整数变量的大小 (当相减时需要判断二者大小)
//比较两个大bign变量的大小
int cmp(bign a, bign b) {
if (a.len > b.len) return 1;
else if(a.len < b.len) return -1;
else {
for (int i = a.len - 1; i >= 0; i--) {
if (a.d[i] > b.d[i]) return 1; //只要有一位a大则a大
else if (a.d[i] < b.d[i]) return -1; //只要有一位a小则a小
}
return 0; //两数相等
}
}4.大整数的输出
void print(bign a) { //输出bign
for (int i = a.len - 1; i >= 0; i--) {
printf("%d", a.d[i]);
}
printf("\n");
}5.高精度加法
以147 + 65 为例,下面来回顾一下小学时候是怎么学习两个整数相加的
① 7 + 5 = 12,取个位数2作为该位的结果,取十位数1进位
② 4 + 6 = 10,加上进位1为11,取个位数1作为该位的结果,取十位数1进位
③ 1 + 0 = 1, 加上进位1为2,取个位数2作为该位的结果,由于十位数为0因此不进位
由此可以归纳:将该位置上的两个数字相加,得到的结果取个位数作为该位结果,取十位作为新的进位,高精度加法的做法与次完全相同,可以来看实现的代码
//高精度加法
bign add(bign a, bign b) {
bign c;
int carry = 0;//进位
for (int i = 0; i < a.len || i < b.len; i++) {
int temp = a.d[i] + b.d[i] + carry; //两个对应进位相加
c.d[c.len++] = temp % 10; //个位数为该位结果
carry = temp / 10; //十位数为新进的位
}
if (carry != 0) { //如果最后进位不为0,则直接赋值给结果的最高位
c.d[c.len++] = carry;
}
return c;
}6.高精度减法
以145 - 67 为例,再来回顾一下小学时候是如何学习两个整数相减的
① 5 - 7 < 0, 不够减,因此从高位4借1,于是4减1变成3,该位结果为15 - 7 = 8
② 3 - 6 < 0, 不够减,因此继续从高位1借1,于是1减1变成1,该位结果变为13 - 6 = 7
③ 上面和下面均为0,结束计算
由此可以归纳:从低位开始比较被减位和减位,如果不够减,则令被减位的高位减1,被减位加10再进行减法,如果够减则直接减,最后一步注意高位后可能有多余的0,要忽视它们,但也要保证结果至少有一位数。代码实现如下
//高精度减法
bign sub(bign a, bign b) { // a - b
bign c;
for (int i = 0; i < a.len || i < b.len; i++) { //以较长的为界限
if (a.d[i] < b.d[i]) { //如果不够减
a.d[i + 1]--; //向高位借位
a.d[i] += 10; //当前位置加10
}
c.d[c.len++] = a.d[i] - b.d[i]; //减法结果为当前位结果
}
while (c.len - 1 >= 1 && c.d[c.len - 1] == 0) {
c.len--; //去除高位的0,同时至少保留一位最低位
}
return c;
}7.高精度与低精度的乘法
我们以147 * 35 为例
① 7 * 35 = 245,取个位数5作为该位结果,高位部分24作为进位
② 4 * 35 = 140, 加上进位24 得164, 取个位数字4为该位结果,高位部分16作为进位
③ 1 * 35 = 35, 加上进位16得51, 取个位数1为该位结果,高位部分5作为进位
由此可以归纳:依旧是从低位开始,对应位置相乘,相乘后的结果的个位作为当前位置的结果,高位部分作为新的进位(乘法进位可能不只一位)代码如下
//高精度与低精度的乘法
bign multi(bign a, int b) {
bign c;
int carry = 0; //进位
for (int i = 0; i < a.len; i++) {
int temp = a.d[i] * b + carry;
c.d[c.len++] = temp % 10; //个位作为该位结果
carry = temp / 10; //高位部分作为新的进位
}
while (carry != 0) { //和加法不一样, 乘法的进位可能不止一位,因此用while
c.d[c.len++] = carry % 10;
carry /= 10;
}
return c;
}8.高精度与低精度的除法
① 1 与 7 比较, 不够除,因此该位商为0,余数为1
② 余数1与新位2组合成12, 12 与7 比较,够除,商为1,余数为5
③ 余数5与新位3组合成53, 53与7比较, 够除, 商为7, 余数为4
④ 余数4与新位4组合成44, 44 与7比较, 够除, 商为6, 余数为2
由此可以归纳:上一步得余数*10加上该步的位,得到该步临时的被除数,将其与除数进行比较:如果不够除,则该位的商为0; 如果够除,则商即为对应的商,余数即为对应的余数,最后一步要注意高位可能有多余的0,要忽视它们但也要保证结果至少有一位数
代码如下
//高精度与低精度的除法
bign divide(bign a, int b, int& r) {
bign c;
c.len = a.len; //被除数的每一位和商的每一位是一一对应的,因此先令长度相等
for (int i = a.len - 1; i >= 0; i--) {
r = r * 10 + a.d[i];
if (r < b) c.d[i] = 0; //不够除,该位为0
else {
c.d[i] = r / b; //商
r = r % b; //获得新的余数
}
}
while (c.len - 1 >= 1 && c.d[c.len - 1] == 0) {
c.len--; //去除最高位的0,同时保留最低位
}
return c;
}
9.完整代码
#define _CRT_SECURE_NO_WARNINGS
#include
#include
using namespace std;
//大整数结构体
struct bign {
int d[1000];
int len;
bign() {//初始化结构体
memset(d, 0, sizeof(d));
len = 0;
}
};
//输入大整数
bign change(char str[]) { //将整数转换为bign
bign a;
a.len = strlen(str);
for (int i = 0; i < a.len; i++) {
a.d[i] = str[a.len - 1 - i] - '0';//逆序赋值
}
return a;
}
//比较两个大bign变量的大小
int cmp(bign a, bign b) {
if (a.len > b.len) return 1;
else if (a.len < b.len) return -1;
else {
for (int i = a.len - 1; i >= 0; i--) {
if (a.d[i] > b.d[i]) return 1;//只要有一位a大则a大
else if (a.d[i] < b.d[i]) return -1;//只要有一位a小则a小
}
return 0;//两数相等
}
}
void print(bign a) { //输出bign
for (int i = a.len - 1; i >= 0; i--) {
printf("%d", a.d[i]);
}
printf("\n");
}
//高精度加法
bign add(bign a, bign b) {
bign c;
int carry = 0;//进位
for (int i = 0; i < a.len || i < b.len; i++) {
int temp = a.d[i] + b.d[i] + carry;//两个对应进位相加
c.d[c.len++] = temp % 10;//个位数为该位结果
carry = temp / 10;//十位数为新进的位
}
if (carry != 0) {//如果最后进位不为0,则直接赋值给结果的最高位
c.d[c.len++] = carry;
}
return c;
}
//高精度减法
bign sub(bign a, bign b) { // a - b
bign c;
for (int i = 0; i < a.len || i < b.len; i++) { //以较长的为界限
if (a.d[i] < b.d[i]) { //如果不够减
a.d[i + 1]--; //向高位借位
a.d[i] += 10; //当前位置加10
}
c.d[c.len++] = a.d[i] - b.d[i]; //减法结果为当前位结果
}
while (c.len - 1 >= 1 && c.d[c.len - 1] == 0) {
c.len--; //去除高位的0,同时至少保留一位最低位
}
return c;
}
//高精度与低精度的乘法
bign multi(bign a, int b) {
bign c;
int carry = 0; //进位
for (int i = 0; i < a.len; i++) {
int temp = a.d[i] * b + carry;
c.d[c.len++] = temp % 10; //个位作为该位结果
carry = temp / 10; //高位部分作为新的进位
}
while (carry != 0) { //和加法不一样, 乘法的进位可能不止一位,因此用while
c.d[c.len++] = carry % 10;
carry /= 10;
}
return c;
}
//高精度与低精度的除法
bign divide(bign a, int b, int &r) {
bign c;
c.len = a.len; //被除数的每一位和商的每一位是一一对应的,因此先令长度相等
for (int i = a.len - 1; i >= 0; i--) {
r = r * 10 + a.d[i];
if (r < b) c.d[i] = 0; //不够除,该位为0
else {
c.d[i] = r / b; //商
r = r % b; //获得新的余数
}
}
while (c.len - 1 >= 1 && c.d[c.len - 1] == 0) {
c.len--; //去除最高位的0,同时保留最低位
}
return c;
}
int main() {
char str1[1000], str2[1000];
printf("请输入两个字符串:");
scanf("%s%s", str1, str2);
bign a = change(str1);
bign b = change(str2);
printf("高精度相加:");
print(add(a, b));
printf("高精度相减:");
if (cmp(a, b) == -1) {
printf("-");
print(sub(b, a));
}
else
print(sub(a, b));
bign x = change(str1);
int y = atoi(str2); //字符串转int
printf("高精度与低精度相乘:"); print(multi(x, y));
int r;
printf("高精度与低精度相除:"); print(divide(x, y, r));
printf("余数:%d", r);
return 0;
}