编辑距离优化(空间和时间)
编辑距离算法
- 编辑距离是计算字符串相似度的算法
-
- 基本代码
- 空间优化
- 时间优化
-
- 参考链接
编辑距离是计算字符串相似度的算法
其原理简单,就是一个字符变到另外一个字符需要增加或者删除或者替换3种操作
这里只讲解编辑距离的空间优化和时间优化
编辑距离leetcode
基本代码
int min(int x,int y, int z) {
if (x > y) {
return y > z? z:y;
} else {
return x > z? z:x;
}
}
int minDistance(string word1, string word2) {
if(word1.size() > word2.size()){
swap(word1,word2);
}
size_t len1 = word1.size();
size_t len2 = word2.size();
vector > edit(len1+1, vector (len2+1,0));
for(int i = 0; i < len1 + 1; i++){
edit[i][0] = i;
}
for(int i = 0; i < len2 + 1; i++){
edit[0][i] = i;
}
for(int i = 1; i < len1+1; i++){
for(int j = 1; j < len2+1; j++){
int mod = edit[i-1][j-1];
if(word1[i-1]!=word2[j-1]){
mod++;
}
edit[i][j] = min(edit[i-1][j]+1,edit[i][j-1]+1, mod);
}
}
return edit[len1][len2];
}
空间优化
从上述基本代码中可以看出,编辑距离占用的内存非常大,为O(m*n)的空间,当比较非常长的字符串时,不适用,其实观察可以发现,每次计算时只需保持上一行和左侧一列的编辑距离,以及左上斜对角的那个编辑距离,空间可以优化为O(m+n),
假设当前点为(i,j)我们需要计算当前点的最小编辑距离,需要左侧,上侧,以及左上斜对角的值,我们把edit_row表示当前行左侧的值,edit_col,表示当前列上侧的值,old表示为左上斜对角的值
算法如下
class Solution {
public:
int min(int x, int y, int z){
if(x > y){
return y>z?z:y;
}else{
return x>z?z:x;
}
}
int minDistance(string word1, string word2) {
if(word1.size() > word2.size()){
swap(word1,word2);
}
size_t len1 = word1.size();
size_t len2 = word2.size();
vector edit_col(len2+1,0);
vector edit_row(len1+1,0);
for(int i = 0; i < len2 + 1; i++){
edit_col[i] = i;
}
for(int i = 0; i < len1 + 1; i++){
edit_row[i] = i;
}
for(int i = 1; i < len1+1; i++){
int old = i-1;
for(int j = 1; j < len2+1; j++){
// cout << edit_col[j] << " ";
if(word1[i-1] != word2[j-1]){
old++;
}
int m = min(edit_row[i]+1,old,edit_col[j]+1);
edit_row[i] = m;
old = edit_col[j];
edit_col[j] = m;
}
// cout << endl;
}
return edit_col[len2];
}
};
时间优化
我们知道,两个字符串最大的编辑距离,就是长度较长的那个字符串,如
**str1: “abc”, str2: “defghi”**两个字符串没有任何相同的字符,由str1变到str2,变化为abc改为def,然后增加ghi,编辑距离为str2的长度
根据这一规律,我们可以得到,**当经过某一个字符串的最小编辑距离大于max(str1.length,str2.length)**时,两个字符串的最小编辑距离一定不会经过这个点,因此这个点也不需要计算最小编辑距离,直接使用max(str1.length,str2.length)即可
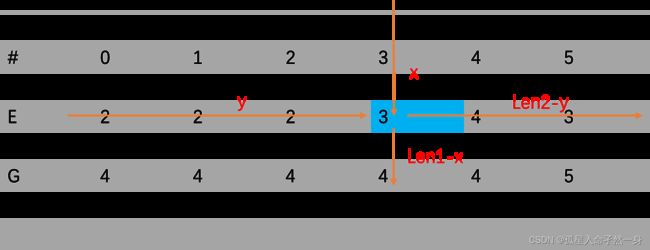
假设其中某一点的坐标为(x,y) ,那么如图所示,经过该点的最小编辑距离计算:
到该点时经过上面的str1的长度为x, 经过左侧的str2 的长度为y,想要距离最短,则需要str1和str2中重合的部分全部相同,即min(x, y )的部分全部相同,那么经过的最短编辑距离为abs(x-y),即 |x - y|, 再看右下部分,
这个点想要到达最右下角,如果min(len2-y, len1 -x)的部分全部相同,则需要的最短编辑距离为|len2-y - (len1 - x)|, 则通过该点由str1变化至str2的最小编辑距离为 |2(x-y)+len2-len1 |
根据之前的规则,由str1变换至str2的最大距离为max(str1.length,str2.length),那么如果经过点(x,y)的最小编辑距离
|2(x-y)+len1-len2 | > max(str1.length,str2.length) 则说明由str1变化至str2的最小编辑距离肯定不是从当前点经过的,那么这个点就可以不用算了,代码如下
int min(int x, int y, int z){
if(x > y){
return y>z?z:y;
}else{
return x>z?z:x;
}
}
int minDistance(string word1, string word2) {
if(word1.size() > word2.size()){
swap(word1,word2);
}
size_t len1 = word1.size();
size_t len2 = word2.size();
int max_edit = max(len1,len2)+1;
vector edit_col(len2+1,0);
vector edit_row(len1+1,0);
for(int i = 0; i < len2 + 1; i++){
edit_col[i] = i;
}
for(int i = 0; i < len1 + 1; i++){
edit_row[i] = i;
}
for(int i = 1; i < len1+1; i++){
int old = i-1;
for(int j = 1; j < len2+1; j++){
int min_edt = (j-i)*2 + len1-len2;
cout << edit_col[j] << "-" << min_edt <<" ";
if(max_edit < std::abs(min_edt)){
old = edit_col[j];
edit_col[j] = max_edit +1;
edit_row[i] = max_edit +1;
continue;
}
if(word1[i-1] != word2[j-1]){
old++;
}
int m = min(edit_row[i]+1,old,edit_col[j]+1);
edit_row[i] = m;
old = edit_col[j];
edit_col[j] = m;
}
cout << endl;
}
return edit_col[len2];
}
参考链接
编辑距离剪枝优化